在存在噪音的情况下改善磁卡读取

大多数磁性读头数据手册没有完全指定频率相关元件，并且在指定其他关键参数时通常含糊不清。在某些情况下，来自两个不同制造商的两个非常相似的磁头的规格在指定和省略的参数方面可能大不相同。数据手册的局限性使得设计最佳的读卡系统变得不必要地困难和耗时。本文档概述了克服上述缺点的策略，并提供了克服噪声问题的指南。

介绍

任何磁卡读卡器 （MCR） 系统最关键的部件之一是磁读头 （MRH）。刷卡时，MRH将卡磁条中存储的数据转换为电压。其他MCR模块处理转换后的电压以提取存储的数据。一张卡与另一张卡之间的磁场强度差异很大，一个人到另一个人的刷卡速度差异使得设计 MCR 并非易事。

MRH数据手册增加了MCR设计的难度，这些数据手册没有完全指定频率相关元件，并且在指定其他关键参数时往往含糊不清。在某些情况下，来自两个不同制造商的两个非常相似的探头的数据手册规格在指定参数列表和省略参数列表中有很大差异。当您试图最大限度地减少MCR系统中的噪声问题时，这些差异尤其麻烦和令人不安。它们无疑使设计最佳的读卡系统变得不必要地困难和耗时。本文概述了解决这些规范问题的策略，然后解释了如何使用针对该任务优化的安全微控制器来优化和克服MCR中的噪声问题。

磁条卡基础知识

图 1 显示了具有三个磁道的磁条卡。一些 ISO/IEC¹ 标准定义了重要的卡属性，例如物理尺寸、条纹的确切位置、磁性属性和磁轨数据结构。轨道 1 标准由国际航空运输协会 （IATA） 创建。轨道2标准由银行业（美国银行家协会，ABA）创建，轨道3标准由储蓄行业创建。

图1.磁条卡。

双频相干相位（F2F）技术用于对磁条卡上的数据进行编码。如图2所示，二进制数据通过磁化具有不同极性的条纹区域沿轨道进行编码。跃迁的极性是任意的，因为只有跃迁之间的相对空间意味着二进制 1 或二进制 0。

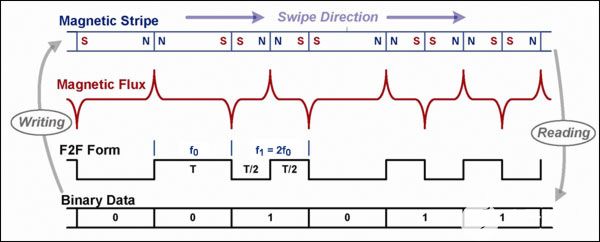
图2.F2F 编码和解码波形。

二进制 0 使用两个单位的条形磁铁进行编码，而一对一个单位的条形表示二进制 1。每个位在条带上占据相同的物理长度。在其长度中间具有额外通量跃迁的位是二进制 1。

采用F2F编码的连续信号的频谱包含两个基频，f0和 f1，其中 f0是二进制 0 和 f 的方波的基本数1= 2f0是二进制 1 的方波的基础。因此，名称为F2F。二进制 0 波形的平均幅度是二进制 1 波形 A 的两倍0= 2A1.

图 3 显示了归一化为 f 的 F2F 编码二进制 0 和 1 的组合频谱0.请注意，大部分信号能量位于f之间0和 3F0.因此，要获得包含一系列 F2F 编码二进制 1 和 0 的矩形波形的良好近似值，恢复两个基本波 （f0和 f1） 和 f 的三次谐波0.

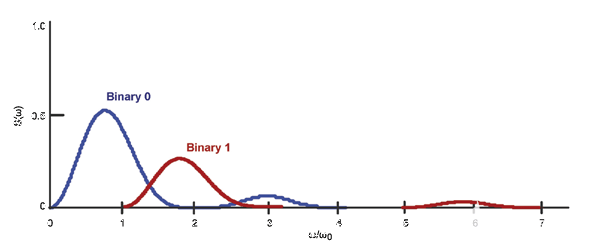
图3.F2F 编码二进制 0 和 1 的频谱。

此外，由于二进制模式不同，f以下还会有其他组件0.然而，我们可以从傅里叶分析中看到，随着频率的降低，这些分量的振幅会迅速减小。因此，带宽从0.5f0至 3F0足以恢复 F2F 编码的矩形波形²。

估计 f 的最小和最大比特率0和 f1，我们需要知道滑动速度范围和轨道记录密度。根据ISO/IEC标准，轨道1和3的记录密度为210位/英寸（8.27位/毫米），而轨道2的记录密度为75位/英寸（2.95位/毫米）。

用于计算 f0，分钟我们采用支持的最慢滑动速度并将其乘以轨道 2 密度数字。对于 f1，最大我们选择支持的最快滑动速度，并将其乘以轨道 1 或 3 的密度。

对于 2 英寸/秒至 100 英寸/秒（5 厘米/秒至 254 厘米/秒）的目标滑动速率，范围为 f0和 f1值计算如下：

轨道 1 和 3：f0，分钟= 0.42kbps 和 f1，最大= 42kbps

轨道 2： f0，分钟= 0.15kbps 和 f1，最大= 15kbps

了解 f 的重要性0，分钟和 f1，最大一旦我们有了MRH模型并研究其传递函数，就会变得清晰。

磁性读头和读卡器基础知识

将磁条卡刷过静止的MRH会导致磁通量发生变化，从而产生移动的电场。因此，在MRH的输出端感应出电压。图2可用于研究读取过程。从顶部开始，经过MRH的磁条会导致磁通事件的变化，从而在MRH的输出端子上感应出电压。没有任何电损耗的开路回读电压由众所周知的表达式给出：³

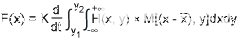
其中：

E（/x.） = 开路电压

K = 与磁条速度、磁头宽度和 MRH 中线圈匝数的影响相关的常数

H（x， y） = 读头的场函数

M［（x - /x.）， y］ = 磁条材料磁化

y1 = 磁条头部到顶部的间距

y2 = 磁条从头部到底部的间距

显然，上述公式非常复杂，对于电路分析和设计来说不是很直观。我们可以使用基本原理来确定模型，如下所示。

MRH将磁能转换为电能。由于MRH的输入是变化的磁场，其输出是变化的电场，因此模型应至少包含一个电感元件Lh和一个电容元件 Ch.在实际系统中，转换过程中总是会消耗一些能量。因此，模型还必须包含一个电阻元件 Rh.在实践中，MRH 不仅具有 Ch在其两个端子上，但它也将具有外部阻抗Zo，例如，来自连接线、PCB 走线、IC 引脚、探头等。

对应于第 n次谐波频率 f 的模型n，如图 4a 所示，然后简化为图 4b。3, 4, 5图2b中二阶电路的传递函数很容易计算如下：

 

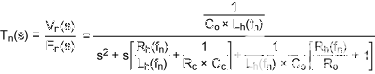
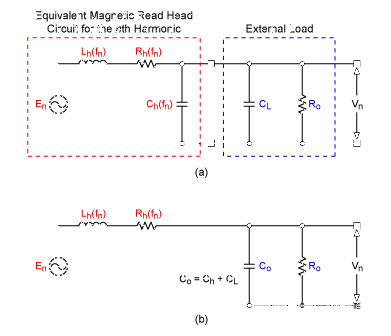
图4.等效的 MRH 模型。

请注意，上述传递函数不包含任何机械或磁性术语，例如滑动速度、头部几何形状、头部和条纹分离以及条纹磁性。因此，传递函数对于电路设计来说更加直观。

为了进一步简化，我们建议使用以最高系统频率为特征的集总模型，而不是将模型限制为滑动速度。

接下来，我们比较一些领先制造商的MRH的电气规格。表 1 列出了图 4b 模型所需的关键规格。请注意不同的细节量。虽然制造商A和C都指定了几个电气参数，但制造商B只指定了一个：峰峰值头读数电平。

 

参数	Manufacturer A	Manufacturer B	Manufacturer C
VO（P-P）（毫伏）	20	19	35
Lh（兆赫）	25	—	110
Ch（pF）	—	—	—
Rh(Ω)	110	—	280

 

关于缺少的信息，可能会出现以下问题。

磁头电感（Lh).L 如何h在更大的频率范围内表现？L 如何h在承载非指定电流时的行为？

磁头直流电阻 （Rh).整个头部端子施加的电压等级是多少？

磁头读取输出电平（VO（P-P）).使用什么类型的测试卡？刷卡速度是多少？头部的负荷是多少？

磁头电容 （Ch).两个头部端子之间的电容是多少？它会随着频率而变化吗？

 

为了理解上述参数的重要性，我们检查传递函数的分母，并通过将其设置为零来找到其根：

为了使表达式保持简单并更好地理解二阶行为，几本网络分析书籍6, 7使用标准形式编写方程式。一个标准使用的形式是：

S² + 2α × S + Ωo² = 0

其根源是：

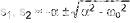
其中：
α是阻尼衰减： 

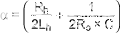
ωo是共振频率：

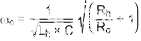
因此，取决于 α 和 ω 的值o，自然反应的根源可以是真实的、复杂的或虚构的。对于熟悉其他标准形式的读者，我们现在将阻尼系数定义为 ζ = α/ωo（注意：品质因数Q = 1/2ζ）并使用其他标准形式：

S² + 2ΖΩo× s + ωo² = 0

其根源是：

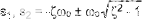
当对系统施加非零强制函数（如阶跃、斜坡或脉冲）时，根在 s 平面中的位置直接影响建立行为。图5显示了在t = 0时施加阶跃时各种ζ值的建立行为。具体而言，建立行为分类如下：

ζ > 1  overdamped
ζ < 1  underdamped
ζ = 1  critically damped
ζ = 0  undamped or oscillatory

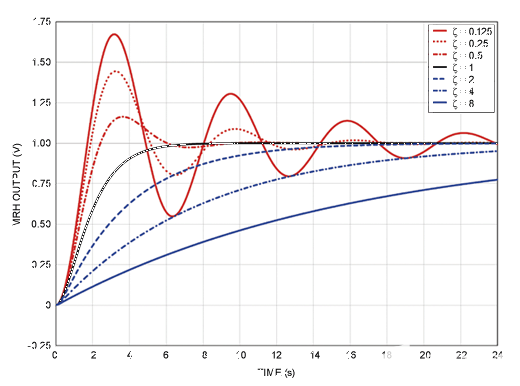
图5.各种ζ值的MRH输出电压。

从图5中，我们观察到在欠阻尼系统中会发生振铃，这可能导致由于假峰值和假过零而导致读数错误。但是，如果系统严重过阻尼，则建立缓慢可能会产生时序误差，峰值偏移可能会产生读数误差。在分析了MRH的时域行为之后，我们接下来看看它的频域行为。

图6显示了传递函数的频率响应，Tn（s），归一化为其共振频率 ωo.当我们接近系统谐振频率时，我们观察到峰值。这是由于图4b所示电路的固有性质，即并行RLC。根据滑动速度，此峰值也可能导致读取错误。

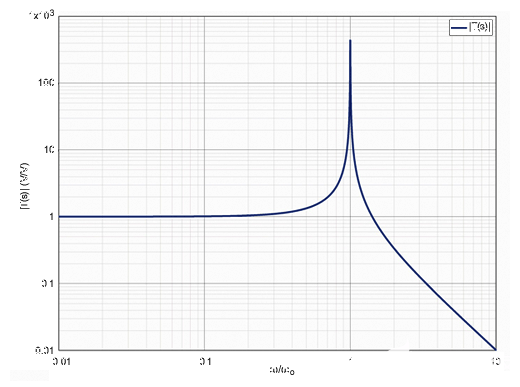
图6.传递函数的频率响应。

回想一下，当尝试恢复 F2F 编码的二进制数据时，我们需要两个基本频率，f0和 f1，至少是f的三次谐波0.从图3可以看出，大部分信号能量都在0.5f附近0至 3.5F0，而一小部分在6F左右0.

如果获得更高的谐波，恢复的F2F波形会发生什么情况？从傅里叶分析中我们知道，恢复的波形形状会随着较高谐波系数的大小变化而变化。因此，在某些情况下，图5所示的增益峰值可能会达到3次和6次谐波被放大到恢复信号严重失真的水平。任何导致假峰和过零的失真都会导致读数错误。

图7强调了上述观点，图<>以数学方式显示了高谐波下两种不同增益的MRH输出电压：蓝色常亮表示单位增益，红色表示增益为<>。黑色虚线是 ZX 迟滞极限。显然，随着增益加倍，红色的MRH输出信号显示出更多的失真、假峰值和过零。

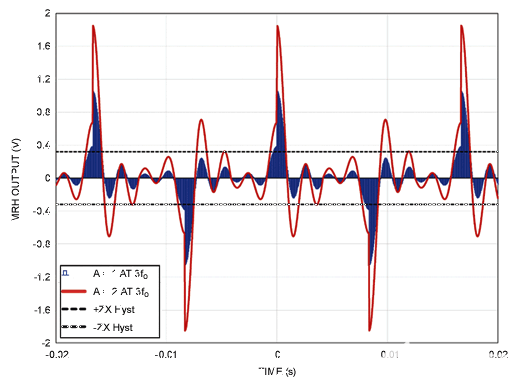
图7.增益峰值引起的MRH输出电压失真。

此外，MRH不仅会因刷卡速度的变化而受到干扰。它还会看到整个系统中可能存在的更高频率的干扰，例如高频系统时钟。由于增益峰值，这也可能导致信号失真和可能的读数错误。因此，为了设计最佳的读卡系统，了解MRH在刷卡速率之外的频率行为至关重要。必须至少在最高系统频率下表征MRH频率行为。

表征各种读头

我们 使用 市售 阻抗 / 增益 相位 分析 仪 来 查找 不同 制造 商 的 多个 MRH 的 等效 电路。表征包括基于DeepCover安全微控制器（MAXQ1740）的MCR中使用的单轨、双轨和三轨MRH。由于12MHz是MAXQ1740的最大系统时钟频率，因此每个MRH的特性范围为100Hz至12MHz（100Hz是分析仪的极限）。表2显示了三轨MRH的参数平均值。®

 

Parameter	MRH 1	MRH 2	MRH 3	MRH 4
Lh（兆赫）	13.67	58.09	13.20	57.43
Ch（pF）	22.15	31.11	20.60	16.97
Rh(Ω)	146.78	234.57	145.72	214.51

 

分析测量参数

比较表2中的参数，我们发现MRH 1和MRH 3非常相似。它们参数之间的相对差异为：ΔLh~ 3.6%， δrh~ 0.7%， 和 ΔCh~ 7.5%。对于 MRH 2 和 MRH 4，其参数的相对差异为：ΔLh~ 1.2%， δrh~ 9.4%， 和 ΔCh~ 83%。由于 Ch影响α和 ωo，对于类似的条件，我们可以预期 MRHs 1 和 3 的行为非常相似。我们可以预期MRHs 2和4的行为会低于它们的共振频率，但随着频率接近和超过它们各自的共振点，它们会发生变化。

当我们绘制表征MRH的传递函数频率响应时，最后两点变得很明显，如图8所示。图8中的负载为1G，阻尼比为0.03。MRHs 1 和 3 的图几乎相同，而 MRHs 2 和 4 的图显示谐振频率差异越来越大。如前所述，幅度的增加可能会导致读取错误。

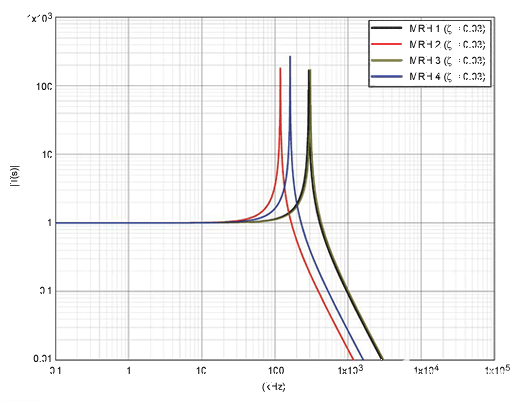
图8.MRH传递函数与1GΩ外部负载下的频率的关系（ζ = 0.03）。

图9显示了150kHz至300kHz频率范围内的MRH传递函数，即对应于最大刷卡速率3in/s（6cm/s）的100次和254次谐波。我们可以看到，随着滑动速率的增加，MRH传递函数幅度值也会增加。这里的主要问题是，如果获得更高的谐波超过一个点，可能会出现错误的过零和峰值，如图7所示。此外，如果大于最大允许的信号出现在磁头和读卡器输入之间的接口上，则可能会发生读取错误。

有两个因素会导致信号较大。首先，更快的滑动会增加磁通量变化的速度。根据法拉第定律，这会产生更大的电感电压，从而导致更大的电感电流。其次，根据欧姆定律，流过较大阻抗的较大电流会产生较大的输出电压。

在刷卡速率范围内，我们需要将峰值限制在小于或等于20，这是MAXQ1740磁卡读卡器的最大和最小增益之比。图9显示，MRHs 1和3的阻抗变化小于20，但MRH 2和MRH 4的变化接近30，超过了20的限制。

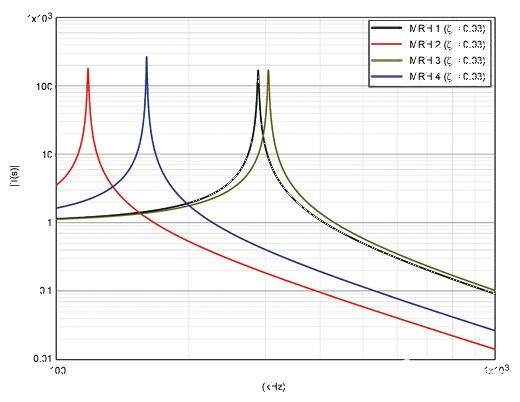
图9.MRH传递函数与3次和6次谐波频率范围的关系。

如果在MRH的输出端增加一个阻尼电阻会发生什么？图10显示了三个任意不同的外部负载值的传递函数图：100kΩ、10kΩ和1kΩ。我们在图10中看到，对于低阻值的外部电阻，与图9所示相比，峰值有所降低。请注意，对于1kΩ负载，所有四个MRH的三次谐波增益都会严重降低。这可能是一个问题。对于 3k 负载，对于 MRHs 100 和 2，增益在 3 次谐波处达到峰值，而对于 MRHs 3 和 2，增益在 3 次谐波处达到峰值。这里的重点是我们不能随意选择 Ro值。

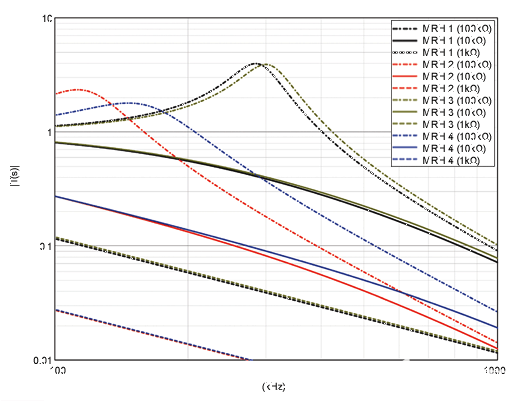
图 10.不同外部负载值的MRH传递函数。

使用外部电阻器 R 时o在MRH端子上，确保阻尼比（ζ）尽可能接近单位非常重要。图 11 绘制了 ζ 与 R 的关系图o对于四种特征的MRH。对于 ζ = 1，我们需要 RoMRHs 12 和 1 的≈ 3kΩ;Ro≈ MRH 22 为 2kΩ;和 RoMRH 28 的≈ 4kΩ。图12显示了具有最佳负载值的传递函数。将图12与图10进行比较，我们注意到增益在三次谐波处没有达到峰值，而是接近单位。

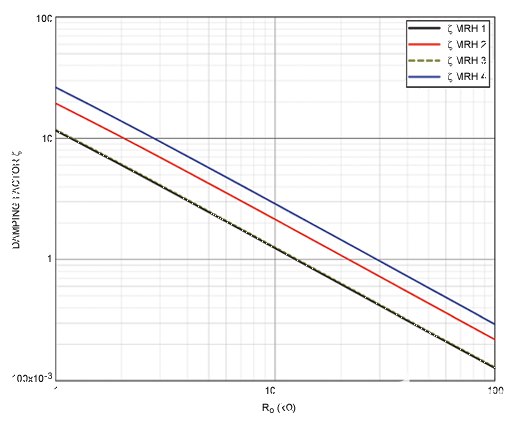
图 11.MRH 阻尼系数 （ζ） 与外部电阻 （Ro).

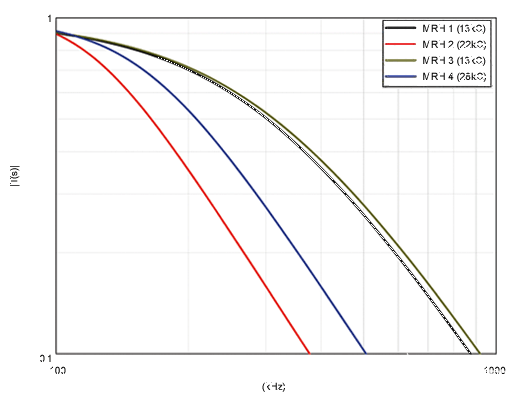
图 12.MRH传递函数可实现最佳外部负载。

虽然最大 Ro由 ζ = 1 设置，最小值 Ro值取决于支持的最小信号和磁头直流电阻，Rh.作为一般规则，保留 Ro≥ 5Rh使 Ro与 R 并行h不会使磁头输出信号衰减超过20%。

这里有几个关键点需要记住。首先，由于并联RLC，传递函数在谐振频率ωo.因此，将此峰值限制在刷卡速率的3次和6次谐波对应的范围内，例如，对于150kHz至300kHz的刷卡速率范围，42kHz至50kHz。其次，可以通过放置R来调整系统行为o穿过读头器的终端。更改 Roζ更改阻尼比。最后，选择 Ro值使系统临界阻尼，并让引线布线和PCB布线设置Co价值。

优化读卡

现在使用一种解决MRH规格差异的方法，我们可以提高读卡性能。我们的重点是减少主要影响过零（ZX）的噪声的影响。在整个频率范围内表征MRH模型后（注意：表征必须包括引线和PCB布线），我们遵循以下步骤。

第 1 步。选择一个 Ro值以获得适当的阻尼比并限制增益峰值。

通常，目标应是临界阻尼到略微过阻尼的系统。作为例外，如果在某些情况下，三次谐波的增益降至一半以下，那么我们可以通过稍微欠阻尼的系统来均衡增益。

欠阻尼系统可能会引入输入信号振铃产生的噪声。振铃噪声会对ZX产生不利影响，但也可能导致增益峰值引起的假峰值。

保持 Ro≥ 5Rh最大 Ro设置ζ = 1。

 

第 2 步。在嘈杂的印刷电路板（PCB）上，它有助于使系统过阻尼，尤其是轨道2（T2）。

T2 有 40 个数字，而 T79/T1 有 3 个字母数字字符。

在T2上，噪声会影响ZX的峰值之间存在较长的间隙。

过阻尼集成了 T2 信号。信号接近锯齿波形，如图13所示。过阻尼通过过滤掉高频毛刺来帮助ZX。

保持 Ro≥ 5Rh使磁头衰减保持在20%以下。

需要注意的是：过度阻尼的系统可能会由于建立缓慢和峰值偏移而导致误差。

 

第 3 步。如果使用较便宜但噪声较大的读头，则通过降低输入信号来克服噪声，而不会影响阻尼比。

选择合适的 Ro.

除以 Ro分成更小的段，使总 Ro与步骤 1 中相同。

使用适当的抽头获取所需的信号分频。

有几种方法可以做到这一点，如下面的实际示例部分所述。

 

第 4 步。当MAXQ1740的读头输出超过300mV时Q-1，发生信号的内部削波。这种剪切也可能导致读取错误。

使用步骤 3 中描述的方法减少信号。

实例

输入信号和降噪

假设优化的输出电阻值为Ro.

目标：信号减少 25%。

使用一个 0.25 × Ro和一个 0.75 × Ro串联在头上。然后 0.75 × Ro系在头部共销侧。将中点绑定到输入。

使用四个 0.25 × Ro串联在头上。将中点绑定到输入。

 

目标：信号减少 75%。

使用一个 0.25 × Ro和一个 0.75 × Ro串联在头上。然后 0.25 × Ro系在头部共销侧。将中点绑定到输入。

使用四个 0.25 × Ro串联在头上。将中点上方的一个水龙头连接到输入。

阻尼系数的影响

接下来，我们考虑使用基于MAXQ1740的MCR刷卡时的各种阻尼因素及其对实际信号行为的影响。MRH 2用于测试。关于使用的测试卡，有两件重要的事情需要注意。首先，卡可从Q-Card购买，并遵循ISO / IEC 7811至7816标准。其次，卡信号幅度指定为标称电平的百分比。因此，40%的卡意味着最大输出电平是标称ISO水平的40%。

在我们获得MRH模型之前，需要费时且令人沮丧的猜测来确定外部电阻的正确值。使用此处提供的模型，我们通过使用与我们的模型预测相匹配的13.5kΩ外部电阻解决了噪声问题。图13显示了过阻尼行为，而图14显示了临界阻尼行为。比较图11和图12，我们注意到与临界阻尼行为相比，过阻尼情况的建立和峰值偏移缓慢。如前所述，缓慢建立和峰值偏移都可能导致时序误差，从而导致读取误差。

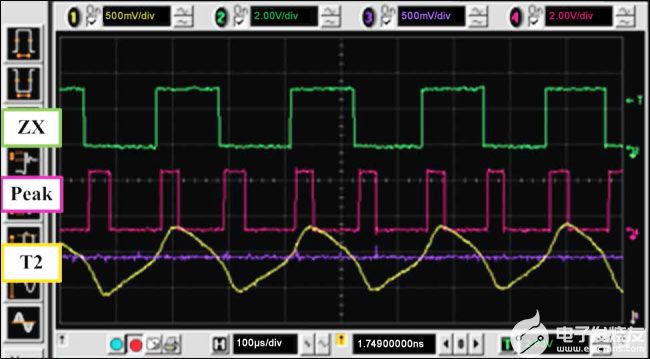
图 13.过阻尼响应。T2 用于使用 40% 卡和 R 手动刷卡o= 1.5kΩ。

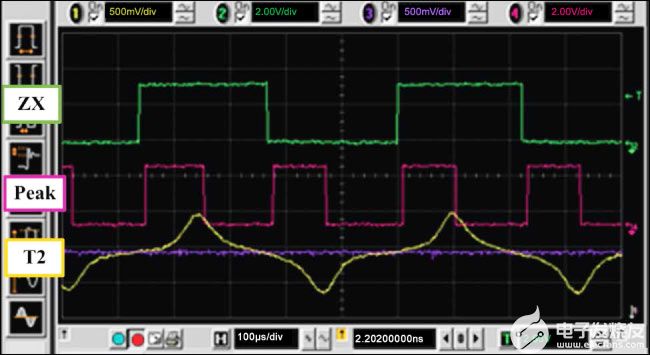
图 14.临界阻尼行为。T2 用于使用 40% 卡和 R 手动刷卡o= 13.5kΩ。

结论

当然可以使用麦克斯韦场方程、MRH 的几何形状和边界条件来预测 MRH 输出电压行为。然而，这种方法非常复杂，对电路分析、设计和调试的见解有限。相反，我们建议首先表征MRH，然后使用基本电路理论和简单的电路模拟器来分析MCR行为。

使用本文中介绍的方法，可以在设计阶段的早期或决定选择哪种MRH时预测和预防潜在问题。例如，设计人员现在可以预见，在欠阻尼系统中，由于假峰值和假过零，可能会发生读数错误。振铃和过度增益峰值（在刷卡速度的3次和5次谐波附近）都可能产生假峰值和过零。相反，如果系统严重过阻尼，则由于峰值偏移，可能会发生时序误差。

此处介绍的方法对于提高使用特定读头的现有读卡器系统的性能也很有用。例如，在噪声系统中，可以首先使用多个串联外部电阻使系统严重阻尼，然后从适当节点分接MRH输出以分压MRH输出电平。

最后，在基于MAXQ1740微控制器的实际读卡器系统中验证了该方法。

审核编辑：郭婷