如何做到白平衡？由远及近的几种白平衡介绍

1、为何需要白平衡？

讨论白平衡，那就要从色温(CCT)谈起，色温顾名思义就是色彩的温度，但是这个色温和我们一般所认知的冷色、暖色不同，它指的是一个绝对黑体(物理学家想象出来的)从绝对零度(-273℃)开始持续加温所呈现出来的颜色，譬如在炼钢炉里给一块铁加热，就会从黑->暗红->亮红->金黄，接着就融化了，因为铁的熔点是1535℃，所以更高温度的颜色就看不到。但从焊接用的火可以看到蓝色的火焰，那是更高的温度所辐射出来的颜色。

这些颜色的差异来自于不同波长光线的比例不同，如下图所示，色温低的情况下（红色）波长较长的光线比例较大，反之亦然。那么就造成白色在高色温的光线照射下显得较蓝，在低色温的光线下显得较黄。

将不同色温下的白色在色品图上连接起来就形成了普朗克曲线：

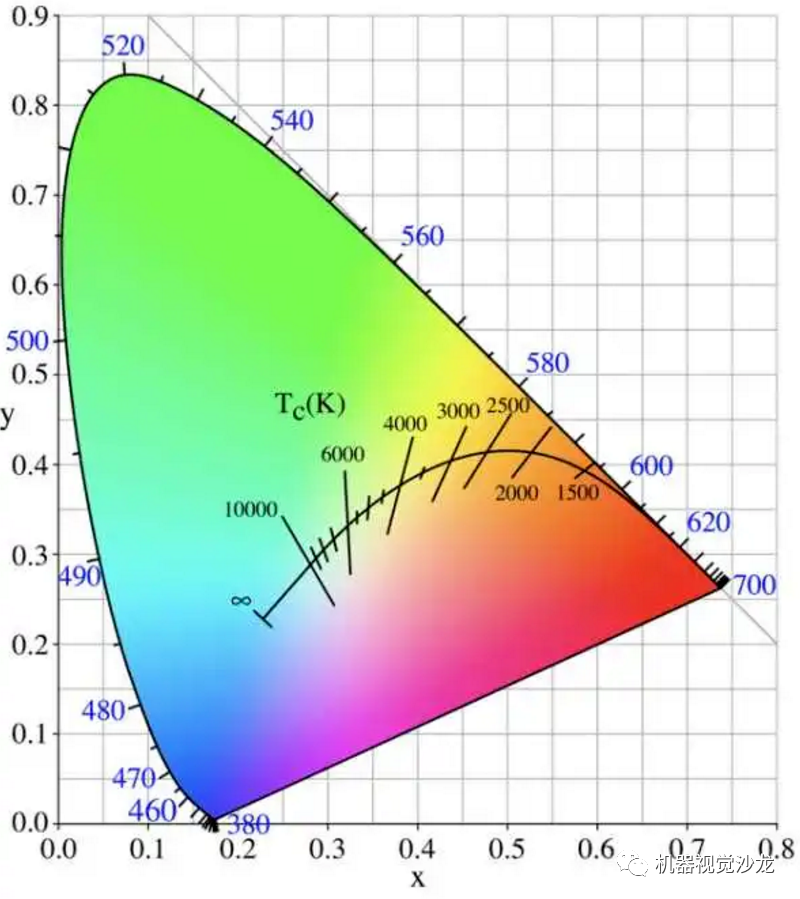
而人眼中的白色总是R = G = B，那么白平衡所做的事情就是在不同色温条件下将图像做归一化，也就是如下将sensor响应的RGB分别乘上一个系数，使得"白色成为白色"。

R‘ = R x R_Gain

G’ = G x G_Gain

B‘ = B x B_Gain

使得R' = G' = B'。

总而言之，白平衡的目的就是让物体在不同光源条件下所呈现出来的颜色，恢复到物体的固有色。

2、白平衡的几种方法

根据白平衡的进化史，下面由远及近介绍了几种白平衡的方法。

2.1 灰世界

最初的白平衡是由Buchsbaum提出的一个叫灰世界的假说而来。这个假说指的是在一副色彩多样的图像中，最终所有颜色的平均统计值应该是一致的，也就是灰色的。

这个假说是由下列的公式推导而出。

f是图像，e(λ)代表入射光频谱，s(λ)代表物体反射率，c(λ)代表sensor的感光度，λ代表波长。

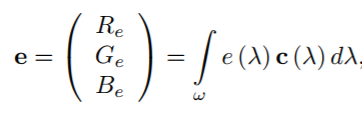
e代表sensor对光源的响应，在特定光源情况下应该是一个常数。

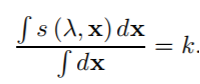
Buchsbaum就提出：一张普通图像的反射率对图像的积分再求平均会是一个恒定值k，也就是说图像的颜色做整体平均后会是一张灰色，也就是无色的图。

将f(x)带入公式后可以做出如下推导：

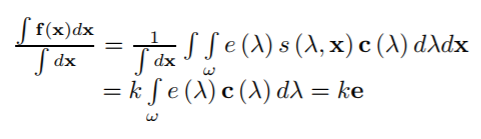
这个方法非常的简单和直观，也是最经典和传统的算法，后续算法都是在此基础上衍生而来。但是此算法有一个致命的缺陷，当背景有大片单一颜色时(比如草地，蓝天等)，该算法就会导致严重的色差。

2.2 完美反射

完美反射法(perfect reflection)基于白色是将光全部反射这个基础上，也就是说图像上如果有白色区域，那么它就会呈现出该色温条件下光原本的颜色，也就是会落在普朗克曲线上。完美反射法可以很大程度的弥补灰世界法的不足，在HDR场景下效果很好，但是依赖于图像中有白色这个前提条件，倘若图像中没有白色，或者噪声很强，方法就会失效。

2.3 早期的白块法

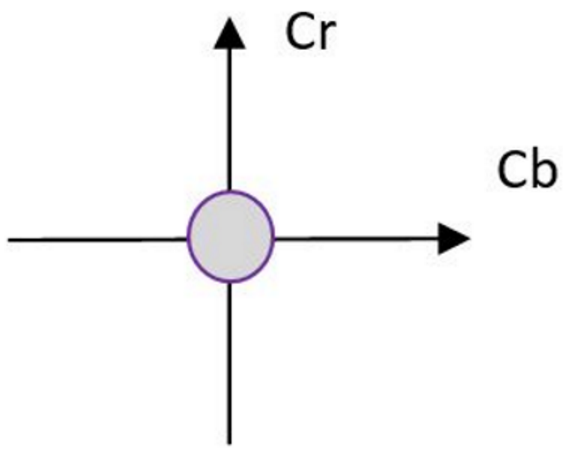
接下来的思路就是如何找到白点/白块。早期的思路是将RGB图像先转换到某个色彩空间，譬如下图中YCbCr，Y是垂直于该平面晚些考虑，那么在原点附近就是色度接近0的区域，也就是我们要寻找的白块。将这个区域内的所有点做一个平均，平均点的坐标就认为是这个图像色温下可能的白色，然后将图像色彩根据平均点做转换，逐步收敛。

设定了区域直径后再考虑Y轴方向，只将最亮的点筛选出来认为是白点。

这个区域的直径也就是该方法主要考虑的问题，设的太大就会导致将原本不是白色的颜色纳入计算也会造成偏差，设的太小就会造成样本量太小。

2.4 基于校准的白块法

白块法在对图像要求比较高的情况下就不适用了，后来就产生了基于校准的白块法。

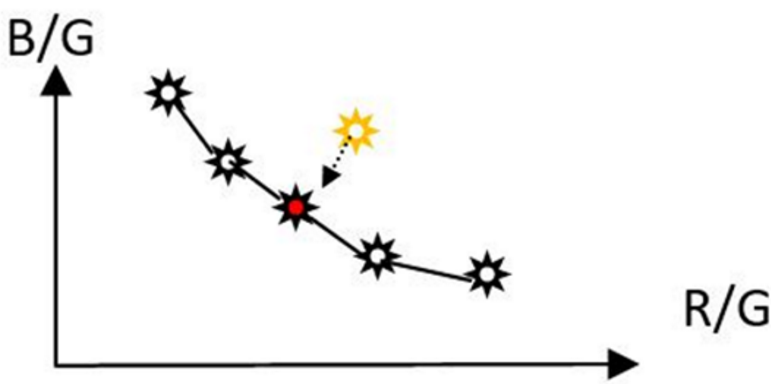
折线上的点是在产线上针对不同光源(D65, A光，H光等)使用标准白/灰卡纸拍出照片算出来的B_gain和R_gain坐标，黄色点是使用白点法实时计算出的坐标，那就找到一个靠近的先验值(红色点)，取该点的gain值。

2.5 加权重白块法

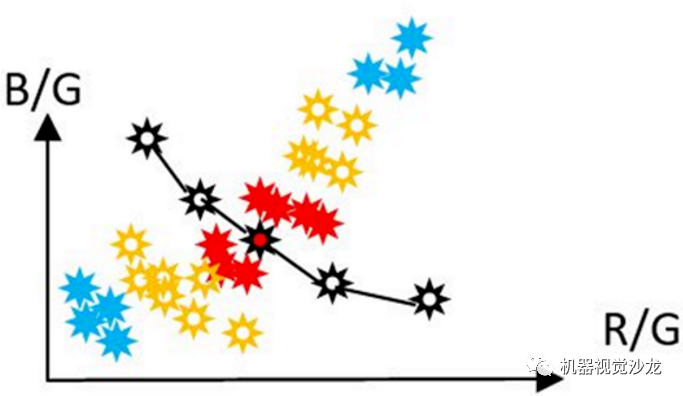
加权白块法就是将图片分为M块，每块都计算出一个白点，将靠近折线区域(红色)的权重加高，远离的(蓝色)权重降低，再计算出一个最终白点，使用折线上的不同点做插值计算出一个最终Gain值。

这个方法的缺点在于校准需要增加产线的大量工作量。

3. 无解的白平衡场景

根据国际电联的标准ITU P910， ITU-R BT500-11，可以归纳出24个典型场景。基本可以分为“有无灰色”，“有无人”，“有无混合光源”，以及“有无大色块”这几种。

以大色块为例，在相同的亮度条件下，机器是无法区分在日光灯下的黄色纸张与白炽灯下的白色纸张。

然而人却能区分，因为人眼有一个叫做视觉恒常性的特点，人判断物体的颜色还有大脑的参与，大脑会透过对环境物体的先验认知来做校准，比如人知道草是绿色，香蕉是黄色。人脑通过这些物体来感知当前的光源情况。

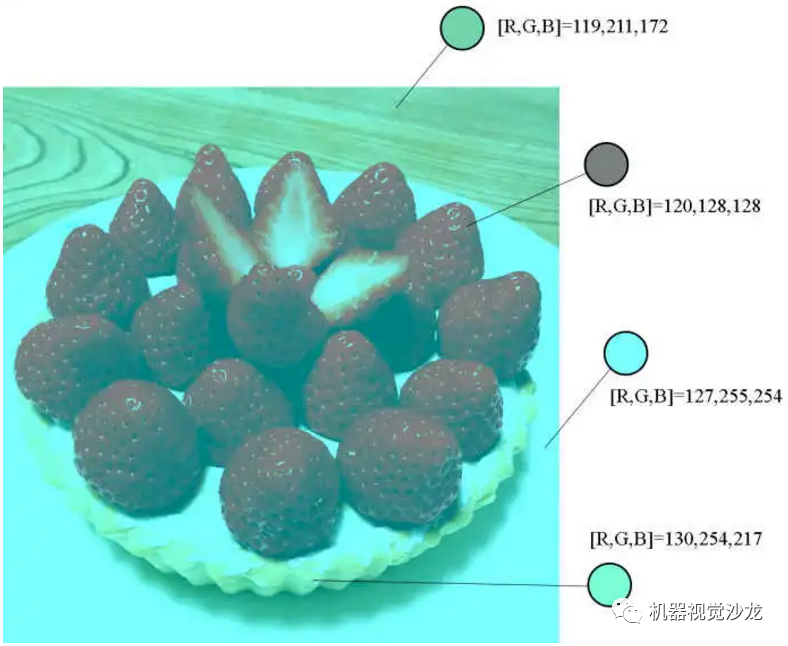
很典型的如下图，实际上图中没有任何红色的像素点，然而人凭借着“草莓是红色的”这个认知做了校准，看到红色草莓，白色盘子和黄色花纹的桌子。这就是根据先验知识来做白平衡的例子。

4. 机器学习带来的希望

在传统的白平衡算法都失效的情况下，机器学习带来了模仿人脑视觉恒常性的希望。

编辑：黄飞