数字信号处理第3部分—傅里叶变换

这篇文章来源于DevicePlus.com英语网站的翻译稿。

在第3部分中，我们的目标是了解如何将正弦信号从时域转换到频域。这个操作过程很重要，因为您可以以此了解在频率范围内可以确定多少信息。例如，ECG（心电图）中如果仅有时域信号，信息量是不够的，因为它只包含了随时间变化的心跳记录（即信号）。但是，在ECG中补充频域分析就能够提供一段时间内信号幅度变化发生次数的有关信息。频域信息以此方式展示了在一定频率范围内，信号在每个给定的频率带是如何分布的。使用傅里叶变换（FT）可以完成时域和频域之间的信号转换。

硬件

• Arduino Uno

• 用于Arduino的MAX9812L驻极体麦克风传感器板

软件

Arduino IDE

MATLAB

步骤 1：傅里叶变换简介

我们首先了解一下相关定义。信号是“传递某种现象的行为或属性信息的一种函数。” 时域表示信号的幅度是如何随时间变化的，而频域则表示随频率变化的幅度频。让我们再次看一下心电图（ECG）示例。心电图显示的是重复的信号波，可以观察到这些信号波的特征是如何随时间变化的（即信号是如何演化的）。很难对一段较长时间内记录的ECG的每个重要成分都进行分析。在这种情况下，您可以将信号转换到频域，并观察在特定时间间隔内重复的每个分量。这就是傅里叶变换的来历。

FT也会在图像和视频压缩中用到。例如，jpg 和 mp3是使用了快速傅里叶变换（FFT）算法的图像和声音的数字格式。由于必须使用模数转换器将每个连续的模拟信号转换为数字信号，所以需要以特定频率对这些信号进行采样。这样，我们可以利用离散傅里叶变换获取离散信号。

傅里叶级数的有趣之处在于，每个波形都可以写成正弦和余弦的总和，但是具有离散频率分量。使用TF，我们可以将波形分解为正弦波。

让我们看一下由多个正弦波组成的信号。该图显示了一个来自现实世界的具有多个频率分量的信号：

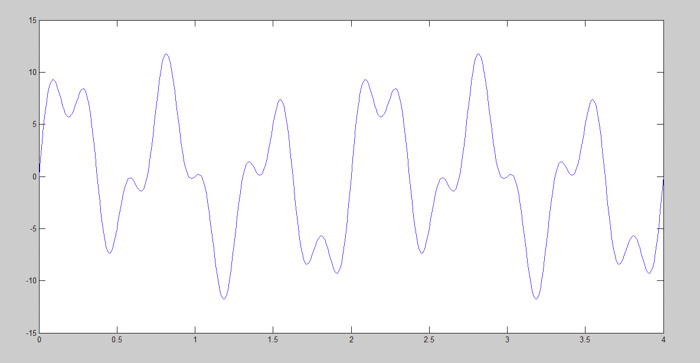
图1：初始信号

我们将会通过下面的所有步骤来逐步添加正弦波，以确定该信号是如何形成的。

f1 = 1;
f2 = 0.5;
f3 = 1.5;
f4 = 4;
t = 0:0.01:4;
A1 = 0.5;
A2 = 2.5;
A3 = 7.5;
A4 = 3.5;

x1 = A1*sin(2*pi*f1*t)
x2 = A2*sin(2*pi*f2*t)
x3 = A3*sin(2*pi*f3*t)
x4 = A4*sin(2*pi*f4*t)

x = x1 + x2+ x3+ x4

添加到图形中的第一个信号如下：

figure %Figure 2
subplot(2,1,1)
plot(t,x,t,x1)
subplot(2,1,2)
plot(t,x1)

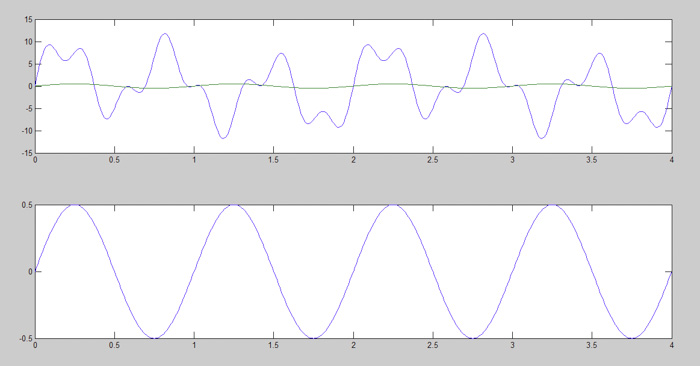
图2：形成图1信号的第1步

在图2中，正弦波（底部）被绘制在初始信号（顶部）中。初始信号还包含许多其它信号。我们将尝试获取顶部图形中的蓝色信号，证明任何信号都可以表示为一些正弦信号之和。

figure %Figure 3
subplot(3,1,1)
plot(t,x,t,x1+x2)
subplot(3,1,2)
plot(t,x2)
subplot(3,1,3)
plot(t,x1+x2)

以下信号应该尽可能接近原始信号。在随后的每个图中将具有以下三个子图：

1.subplot(3,1,1)：在同一坐标图中绘制两个图形，蓝色表示初始信号，由不同频率的正弦波叠加而成，绿色表示获得原始信号之前的所有步骤中所添加信号的总和。

2.subplot(3,1,2)：当前步骤中所添加的信号，由另一个幅度和频率来表达。

3.subplot(3,1,3)：信号总和 – subplot(3,1,1) 中的绿色信号，没有重叠部分。

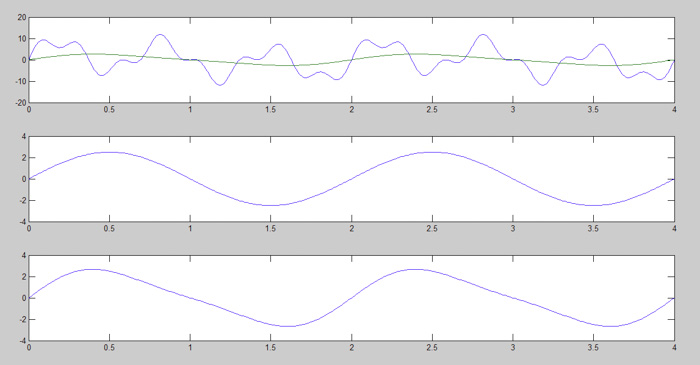
图3：形成初始图像的第2步

从图3中可以看出，信号已经开始形成初始信号的波形。在subplot(3,1,3)中，您可以观察到形状由于添加了更多的信号而发生了变化。从这一步开始，信号不再是标准的正弦曲线形状。

figure %Figure 4
subplot(3,1,1)
plot(t,x,t,x1+x2+x3)
subplot(3,1,2)
plot(t,x3)
subplot(3,1,3)
plot(t,x1+x2+x3)

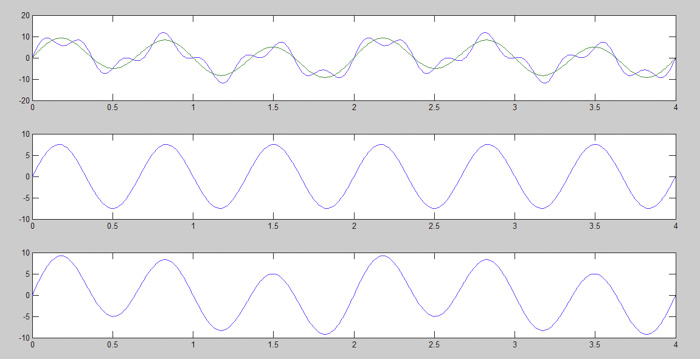
图4：形成原始信号的第3步

在图4中，我们可以观察到subplot (3,1,3)的信号幅度是如何演变的。A3 = 7.5 表明，当添加多个信号时，所得信号的幅值是由每个信号的幅值相加得到的。

figure %Figure 5
subplot(3,1,1)
plot(t,x,t,x1+x2+x3+x4)
subplot(3,1,2)
plot(t,x4)
subplot(3,1,3)
plot(t,x1+x2+x3+x4)

在正弦信号相加过程的最后一步中，演示了原始信号是如何形成的。最后添加的信号相比于上一步中添加的信号具有更高的频率。与上图相比，我们可以观察到图5中的subplot(3,1,3)包含更多的曲线波形。

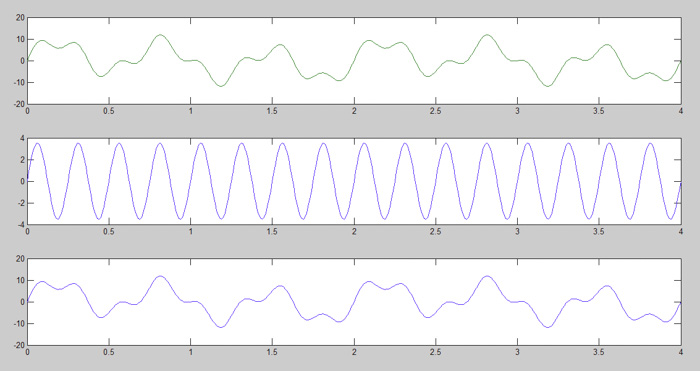
图5：形成原始信号的最后一步

如图5所示，subplot(3,1,1)的绿色信号与subplot(3,1,3)的蓝色信号之间没有任何区别。该示例很重要，因为它展示了傅里叶级数的逻辑，即将一个信号可以描述为不同频率正弦波之和。

傅里叶变换被用于那些需要在频域中执行的操作（例如滤波）。在频域中获得结果后，我们可以将信号转换回时域，以便于在后续处理中使用。

步骤2：背后的算法

复数是傅里叶变换算法中的一个重要概念。复数可以表示为z = a + bi，其中a & b为实数，i是虚数，为x2-1的解（因为该式没有实数解，所以解被认为是虚数）。

下图显示了如何用图形表示复数。您可以通过Argand 图对复数进行几何表示。x轴表示复数的实部，y轴表示复数的虚部。

图6：复数的实部和虚部

时域和频域的每个分量都由包含了N个复数点的信号来描述。每个点都由用于描述信号分量的实部和虚部组成。有一个应用于现实生活中的电气工程领域的实例：使用傅里叶变换可以帮助我们分析变化的电压和电流。

图7： 傅里叶变换中使用的实部和虚部展示

快速傅里叶变换（FFT）的过程是将一个包含N个样本点的时域信号分解为N个时域信号，每个时域信号表示一个样本点信息。第二步是计算这N个时域信号相对应的N个频谱。最后，将N个频谱合为一个频谱。

点击此处可以找到有关傅里叶变换的更多信息。

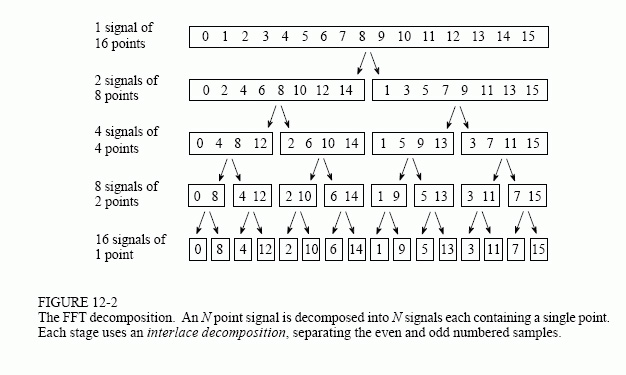
图8：时域分解

使用傅里叶变换时的一些重要规则如下：

• 时域中的点数等于频域中的点数。

• 假设您有一个包含DC值的正弦波 – 频谱中的第一个点将具有零频率值（DC值），而下一个点为正弦频率。

• 当从时域转为频域时，可以使用第n个点的频率进行绘制：f = (n-1) SR/N，其中N为样本点数。

• 频率为f = 1/T，其中T为周期。

让我们来看一下下面的代码，以了解在MATLAB中是如何实现傅里叶变换的。

t = 0:1/1000:1-1/1000;
x = sin(2*pi*30*t);
plot(t,x)

从向量t中可以观察到，点采样是在1/1000范围内进行的，因此采样率为1000 Hz（1000 1s或 s-1）。您还记得之前的文中提到的采样率应该是信号频率的两倍吗？

下面的正弦波的频率为30Hz。

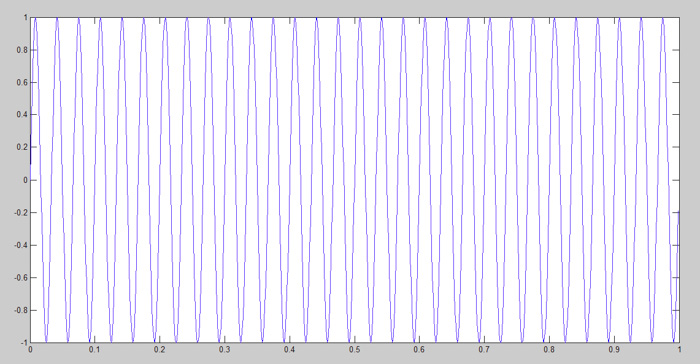
图9：在MATLAB中生成的正弦波

当我们想要进行傅里叶变换时，使用fft(x)指令。

y = fft(x);
f = (0:length(y)-1)*1000/length(y);
plot(f,abs(y))

当我们在频域中绘图时，x轴将除以2。

使用傅里叶变换后，我们只需要一半的采样率即可观察到信号的频谱分量。

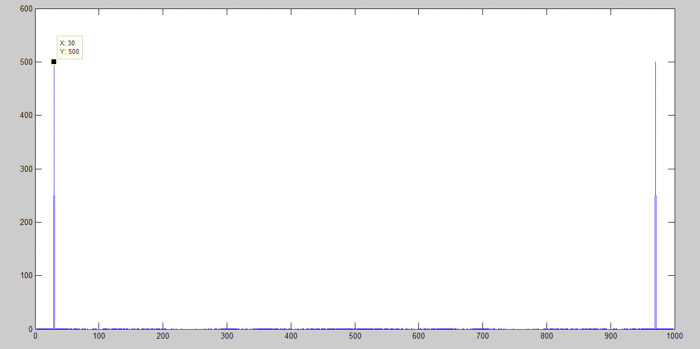
图10：MATLAB中的fft函数图

当在正弦信号上应用FFT时，其唯一的属性是与时域中所描述的频率点相对应的频谱分量，在本例中为30 Hz。

如果将长度指令应用于向量t，则返回：

>> length(t)

ans =

1000

如图 11所示，当我们对所有点进行绘制时，可以观察到一个有趣的现象： 970 Hz(1000-30 Hz)处还有一个频谱分量。这意味着y轴以500 Hz为中心发生了镜像翻转，对应了采样率除以2的结果。

目前为止，我们的项目已经快要完成了。请继续阅读下一篇文章来了解如何添加失真滤波器使信号发生变形。然后，我们将在使用MATLAB创建的GUI上继续对声音信号进行处理。

审核编辑 黄宇