使用ADI公司的有源滤波器设计工具

Hank Zumbahlen

滤波器设计过程包括两个步骤。在步骤1中，确定滤波器的响应，这意味着定义了滤波器的衰减和/或相位响应。在步骤 2 中，定义了筛选器的拓扑（如何构建）。本应用笔记旨在为步骤1提供帮助。讨论了几种不同的标准响应，并介绍了它们的衰减、群延迟、阶跃响应和脉冲响应。然后使用过滤器工具来设计过滤器。提供了一个示例。

标准响应

许多传递函数可用于满足特定滤波器的衰减和/或相位要求。选择的那个将取决于特定的系统。必须确定频域响应与时域响应的重要性。此外，这两者都可能与过滤器的复杂性以及成本进行权衡。

巴特沃斯过滤器

巴特沃兹滤波器是衰减和相位响应之间的最佳折衷方案。它在通带或阻带中没有纹波;因此，它有时被称为最大平坦滤波器。巴特沃兹滤波器以牺牲从通带到阻带的相对较宽的过渡区域为代价来实现其平坦度，具有平均瞬态特性。

与许多其他过滤器类型相比，巴特沃兹滤波器的元素值更实用且不那么重要。频率响应、群延迟、脉冲响应和阶跃响应如图1所示。极点位置和相应的ωo表二列出了α术语。

切比雪夫滤波器

切比雪夫（或切维雪夫、切比切夫、切比舍夫或切维谢夫，取决于俄语的翻译）滤波器的过渡区域比同阶巴特沃斯滤波器小，但代价是其通带中的波纹。该滤波器的名称来自切比雪夫准则，该准则使最大纹波的高度最小化。

切比雪夫滤波器在直流时的相对衰减为0 dB。奇阶滤波器的衰减带从0 dB延伸到纹波值。偶数阶滤波器的增益等于通带纹波。通带中的纹波周期数等于滤波器的阶数。

切比雪夫滤波器通常经过归一化处理，使纹波带的边缘位于ωo= 1。

3 dB带宽由下式给出

表一对此作了列。

图2至图6显示了各种切比雪夫滤波器的频率响应、群延迟、脉冲响应和阶跃响应。极点位置和相应的ωo表三至表七列出了α术语。

 

次序	0.01分贝	0.1分贝	0.25分贝	0.5分贝	1分贝
2	3.30362	1.93432	1.59814	1.38974	1.21763
3	1.87718	1.38899	1.25289	1.16749	1.09487
4	1.46690	1.21310	1.13977	1.09310	1.05300
5	1.29122	1.13472	1.08872	1.05926	1.03381
6	1.19941	1.09293	1.06134	1.04103	1.02344
7	1.14527	1.06800	1.04495	1.03009	1.01721
8	1.11061	1.05193	1.03435	1.02301	1.01316
9	1.08706	1.04095	1.02711	1.01817	1.01040
10	1.07033	1.03313	1.02194	1.01471	1.00842

 

贝塞尔滤波器

巴特沃兹滤波器具有相当好的幅度和瞬态行为。切比雪夫滤波器以牺牲瞬态行为为代价改善了幅度响应。贝塞尔滤波器经过优化，由于通带中的线性相位（即恒定延迟）而获得更好的瞬态响应。这意味着频率响应相对较差（幅度判别较小）。

贝塞尔滤波器的频率响应、群延迟、脉冲响应和阶跃响应如图7所示。极点位置和相应的ωo表八列出了α术语。

具有等纹误差的线性相位

线性相位滤波器在通带内提供线性相位响应，范围比贝塞尔更宽，并且衰减远低于截止。这是通过让相位响应产生波纹来实现的，类似于切比雪夫的振幅纹波。随着纹波的增加，恒定延迟区域进一步延伸到阻带。这也会导致群延迟产生纹波，因为它是相位响应的导数。阶跃响应将显示比贝塞尔略多的过冲，脉冲响应将显示更多的振铃。

误差为0.05°和0.5°的等波滤波器的频率响应、群延迟、脉冲响应和阶跃响应分别如图8和图9所示。极点位置和相应的ωo表九和表X列出了α术语。

瓜西至6 dB和瓜西至12 dB滤波器

高斯至6 dB和高斯至12 dB滤波器是切比雪夫滤波器和高斯滤波器之间的折衷方案，后者类似于贝塞尔滤波器。过渡滤波器在通带中具有近乎线性的相移和平滑、单调的滚降。在通带以上，特别是在较高的n值下，有一个断点，超过该断点，与贝塞尔相比，衰减急剧增加。

高斯至6 dB滤波器在通带内具有比巴特沃兹滤波器更好的瞬态响应。超出断点，发生在 ω 处o= 1.5，滚降类似于巴特沃兹滤波器。

高斯至12 dB滤波器在通带内的瞬态响应比巴特沃兹滤波器好得多。超过12 dB断点，发生在ωo= 2，衰减小于巴特沃兹滤波器。

高斯至6 dB和高斯至12 dB滤波器的频率响应、群延迟、脉冲响应和阶跃响应分别如图10和图11所示。极点位置和相应的ωoα术语列于表十一和表十二。

使用原型响应曲线

前面讨论的几个全极点响应的低通原型的响应曲线和设计表现已编目。所有曲线均归一化为–3 dB截止频率1 Hz。这允许直接比较各种响应。在所有情况下，将显示频率范围为 2.10 Hz 至 0 Hz 的 1 至 10 极情况的幅度响应。然后，将显示0.1 Hz至2 Hz通带的详细信息。还将显示从0.1 Hz到10 Hz的群延迟，脉冲响应以及从0秒到5秒的阶跃响应。

如果要使用曲线来确定现实生活中滤波器的响应，则必须对曲线进行非规范化。在幅度响应的情况下，只需将频率轴乘以所需的截止频率F 即可实现C.要对群延迟曲线进行非规范化，请将延迟轴除以 2π FC并将频率轴乘以 FC.通过将时间轴除以 2π F 来非规范化阶跃响应C.通过将时间轴除以 2π FC 并将幅度轴乘以 2π F 来非规范化脉冲响应C.

对于高通滤波器，只需反转幅度响应的频率轴即可。在将低通滤波器转换为高通滤波器时，瞬态行为不会保留。兹维列夫提供了一种计算这些响应的计算方法。

在将低通转换为窄带通时，0 Hz轴移动到中心频率F0.按理说，带通情况在中心频率周围的响应将与0 Hz附近的低通响应相匹配。低通滤波器的频率响应曲线实际上反映在0 Hz附近，尽管我们通常不关心负频率。

要使带通滤波器的群延迟曲线非规范化，请将延迟轴除以πBW，其中BW是以Hz为单位的3 dB带宽。然后，将频率轴乘以 BW/2。一般来说，带通滤波器在F处的延迟0在 0 Hz 时，延迟将是具有相同带宽的低通原型的两倍。这是因为低通到带通变换会产生阶数为2n的滤波器，尽管它通常被称为与我们派生它的低通滤波器具有相同的阶数。这种近似值适用于窄带滤波器。随着滤波器带宽的增加，曲线会发生一些失真。延迟变得不对称，峰值低于F0.

带通滤波器的响应包络类似于低通原型的阶跃响应。更确切地说，它几乎与带宽一半的低通滤波器的阶跃响应相同。要确定带通滤波器的包络响应，请将低通原型阶跃响应的时间轴除以πBW，其中BW是3 dB带宽。之前关于过冲、振铃等的讨论现在可以应用于载波包络。

窄带带通滤波器对载波短脉冲串（突发宽度远小于带通滤波器非归一化阶跃响应的上升时间）的响应包络可以通过对低通原型的脉冲响应进行非归一化来确定。为此，将振幅轴乘以时间轴除以 πBW，其中 BW 是 3 dB 带宽。假设载波频率足够高，以便在突发间隔期间发生许多周期。

虽然群延迟、步进和脉冲曲线不能直接用于预测滤波器引起的波形失真，但在用于比较滤波器时，它们是一个有用的品质因数。

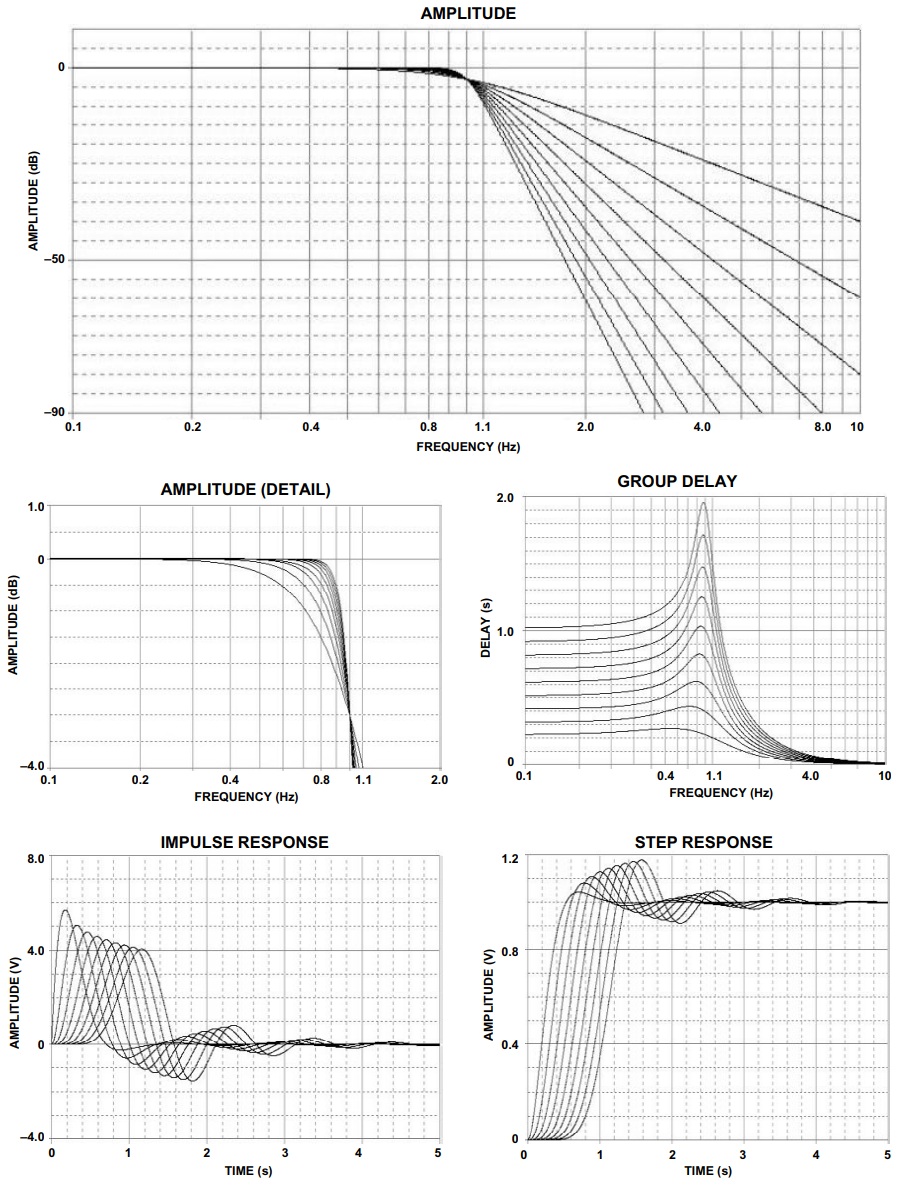
图1.巴特沃思回应

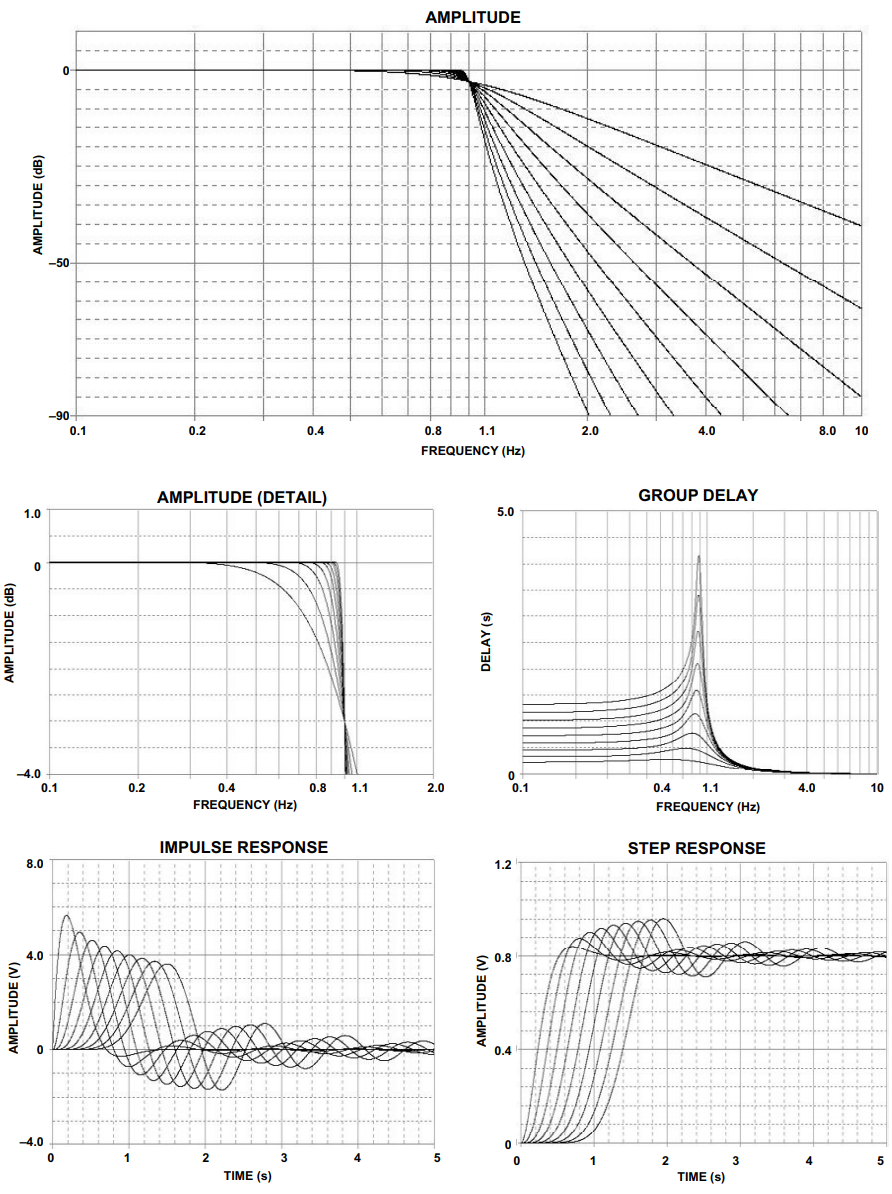
图2.0.01 dB 切比雪夫响应

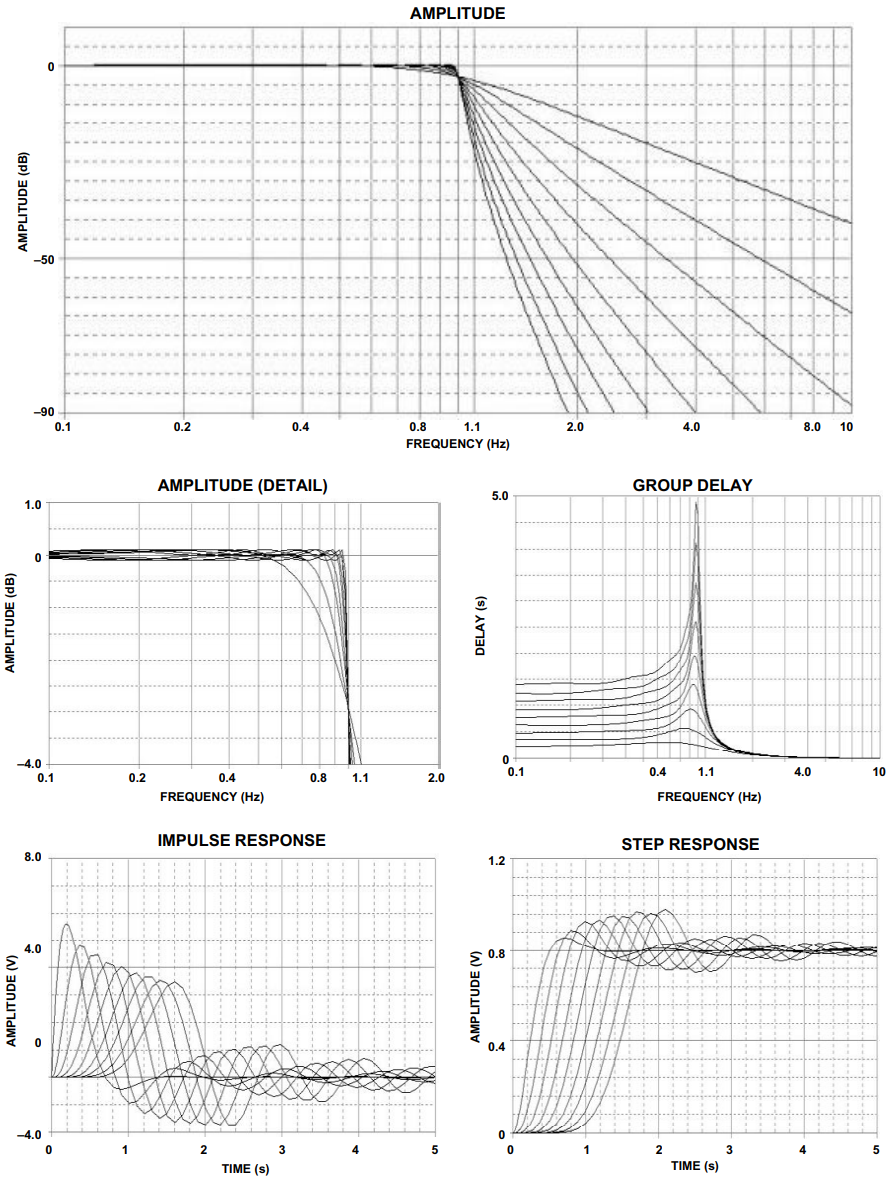
图3.0.1 dB 切比雪夫响应

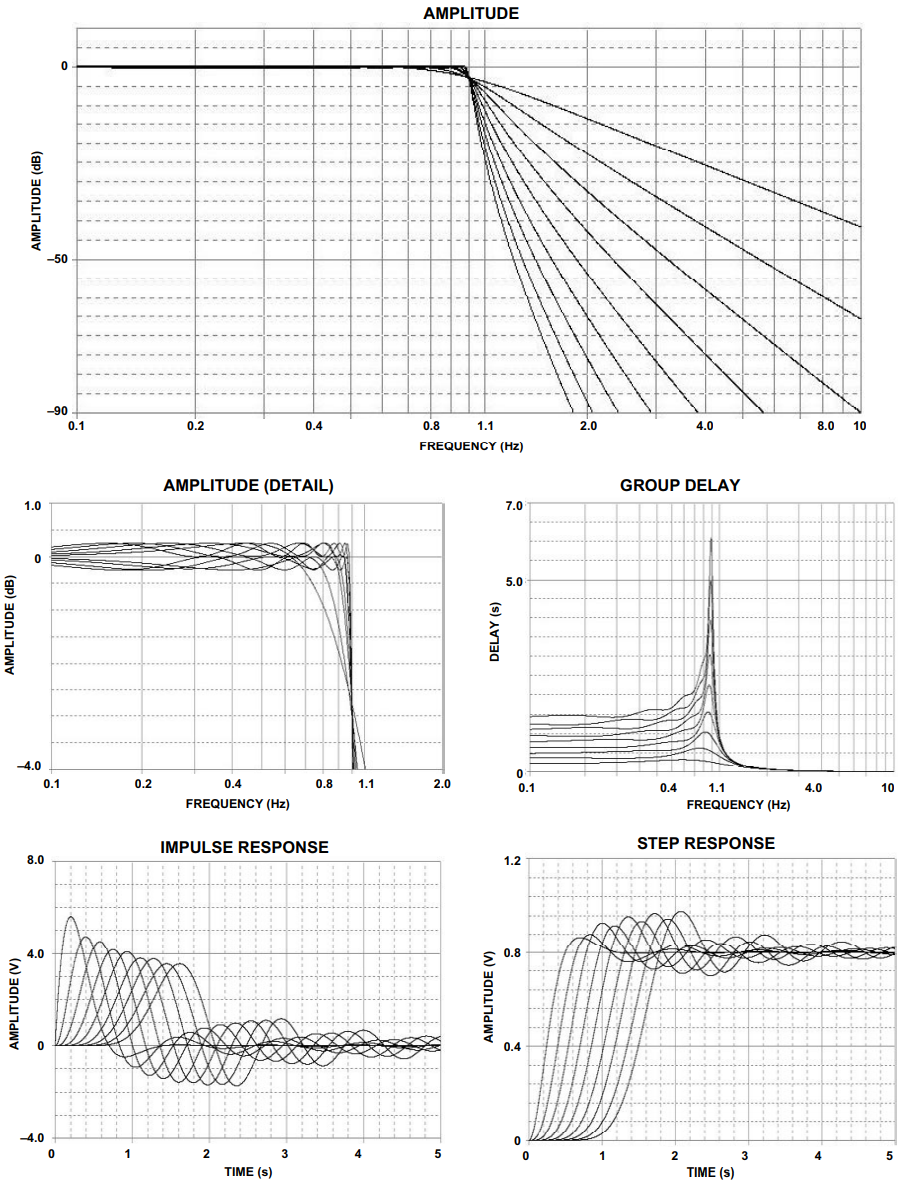
图4.0.25 dB 切比雪夫响应

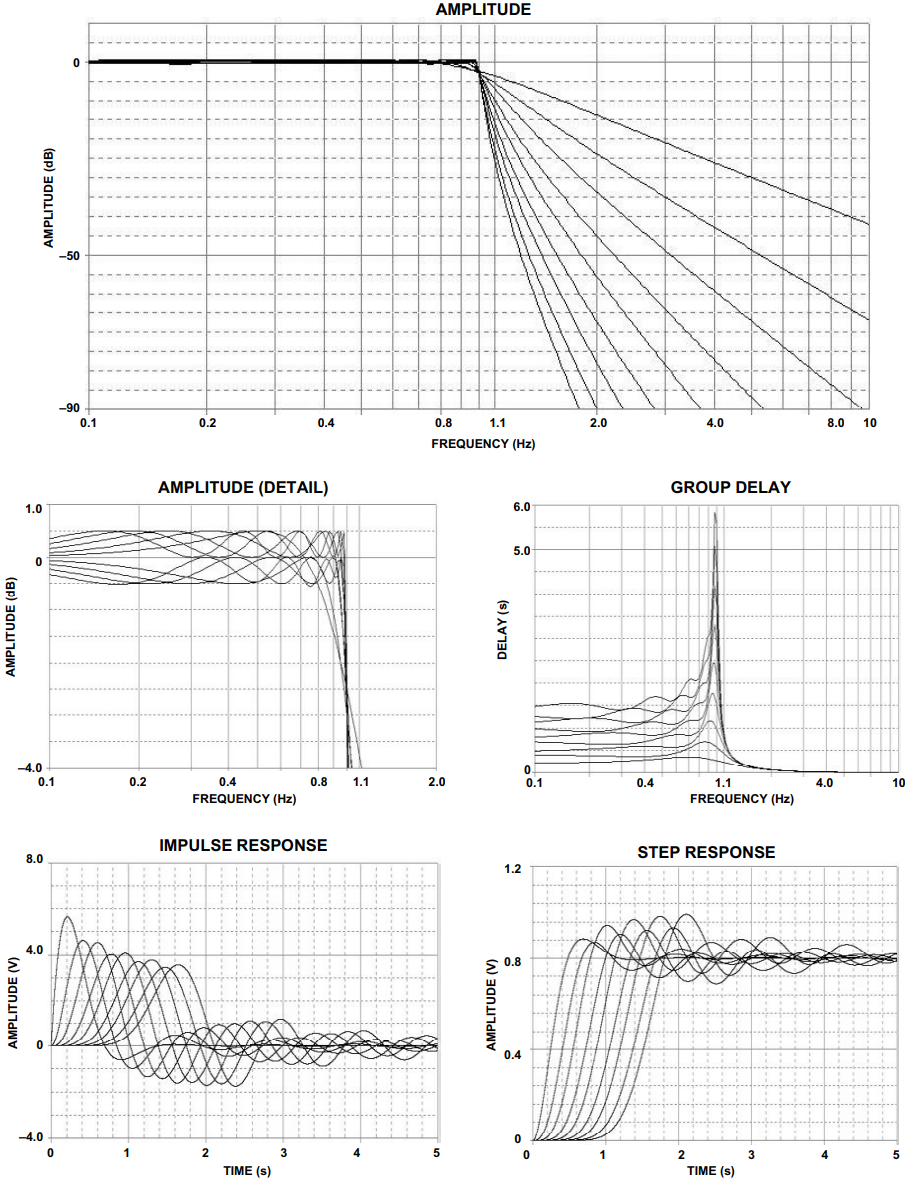
图5.0.5 dB 切比雪夫响应

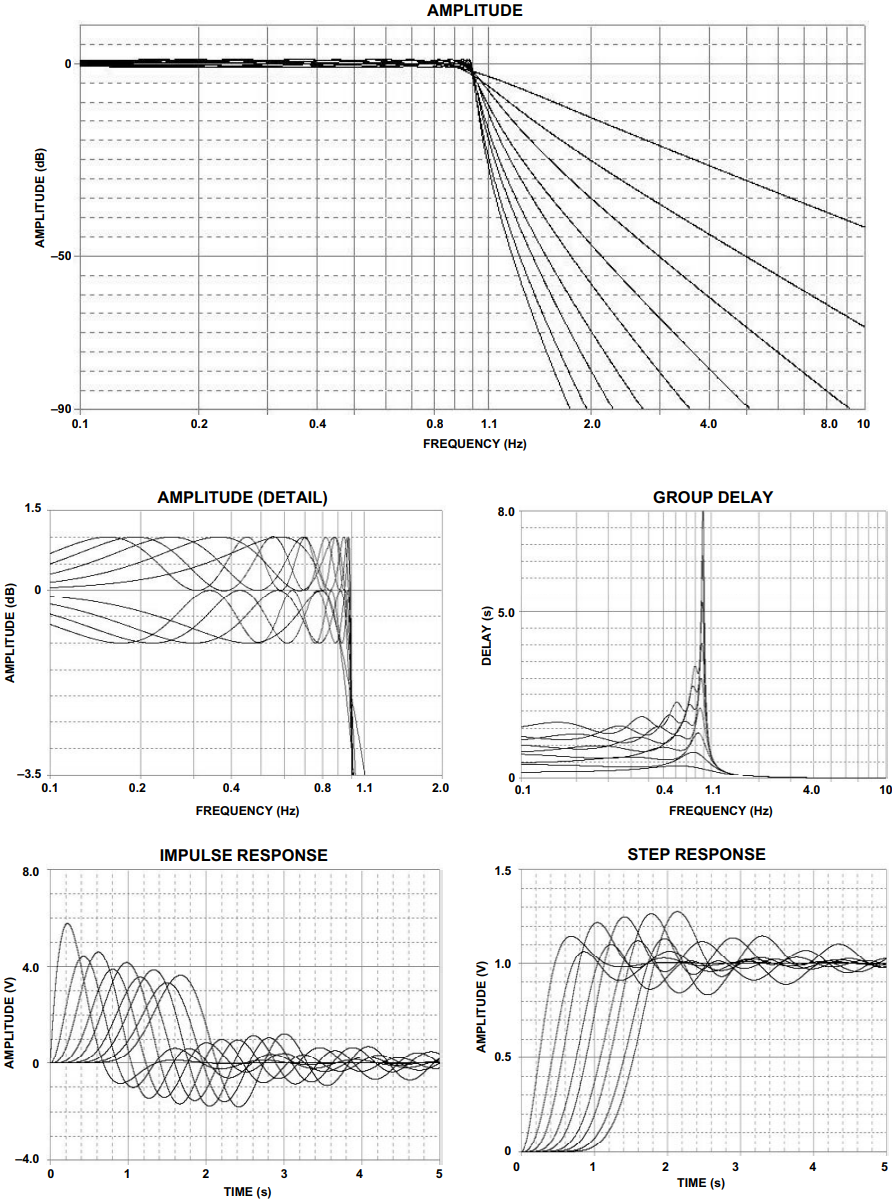
图6.1 dB 切比雪夫响应

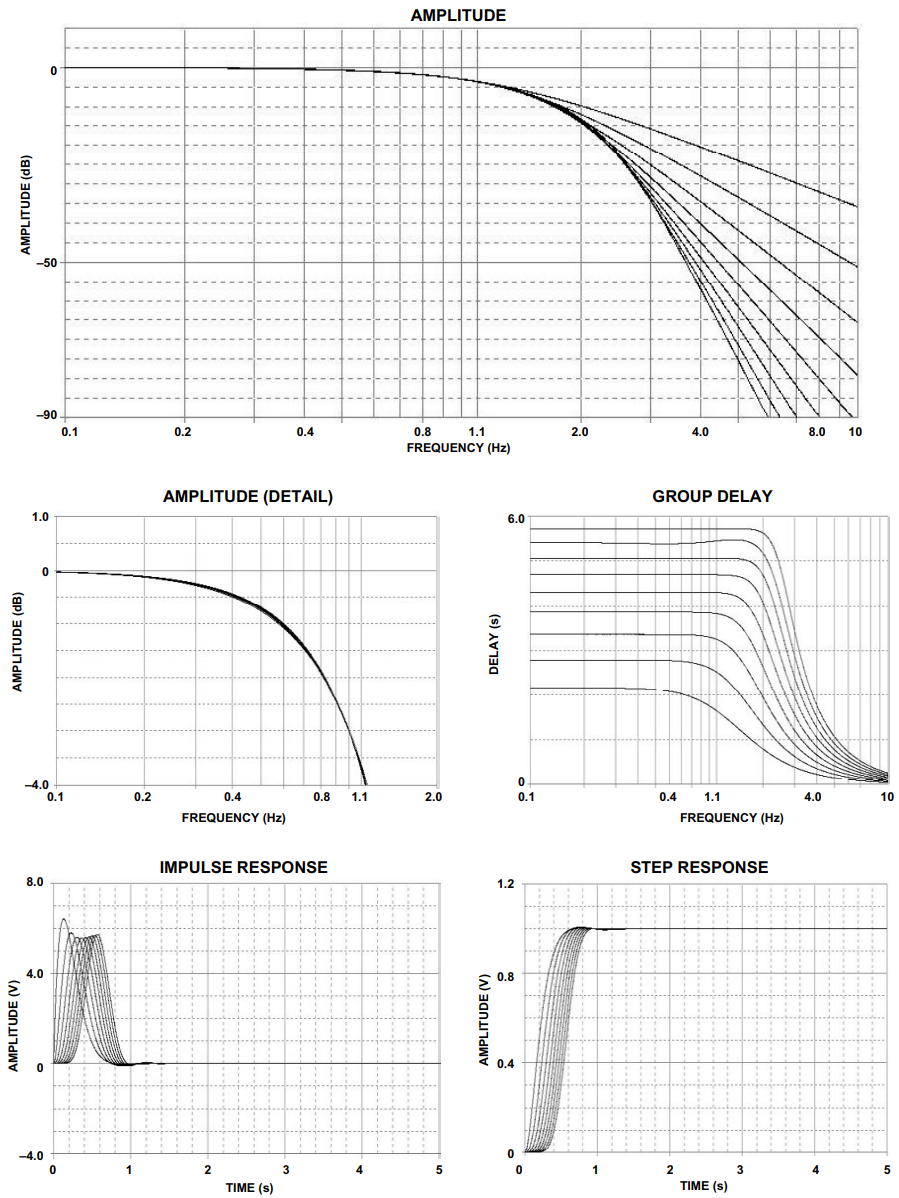
图7.贝塞尔回应

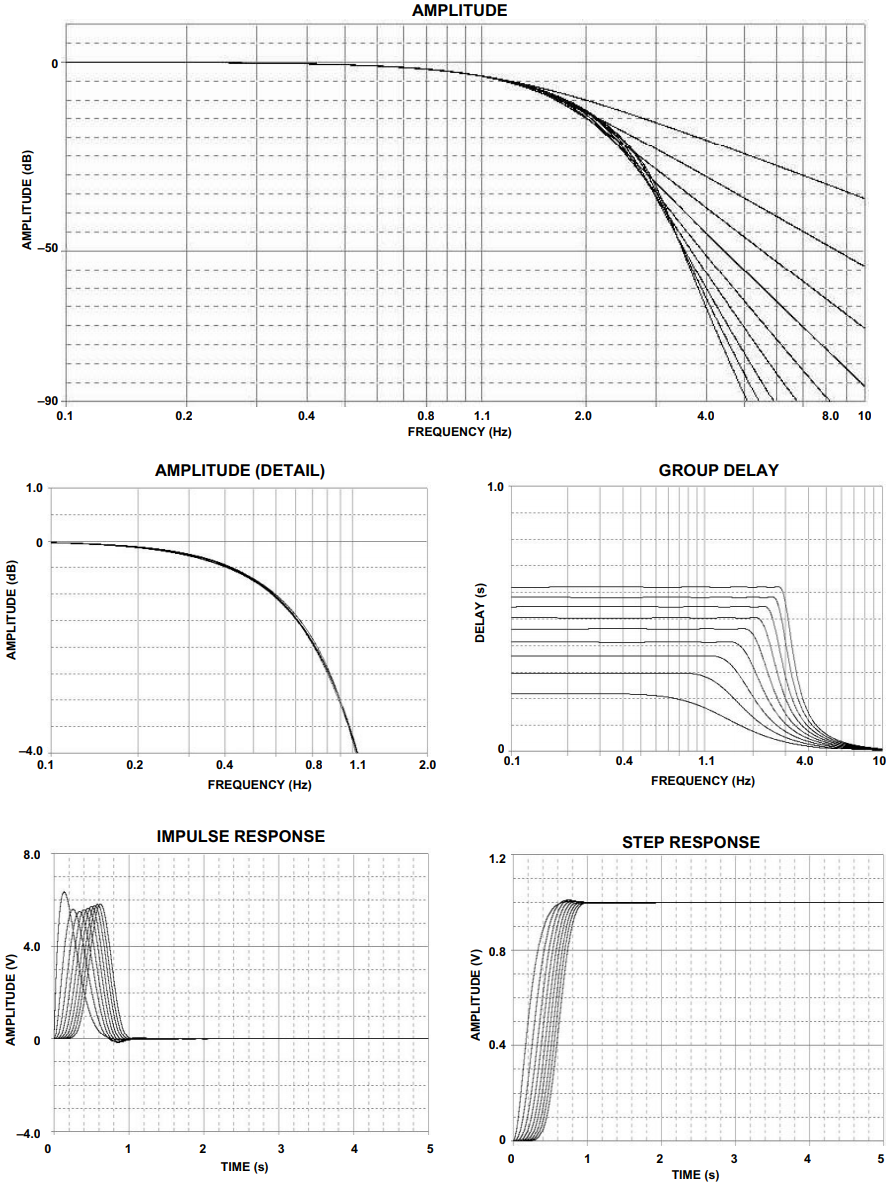
图8.线性相位，等纹误差为0.05°响应

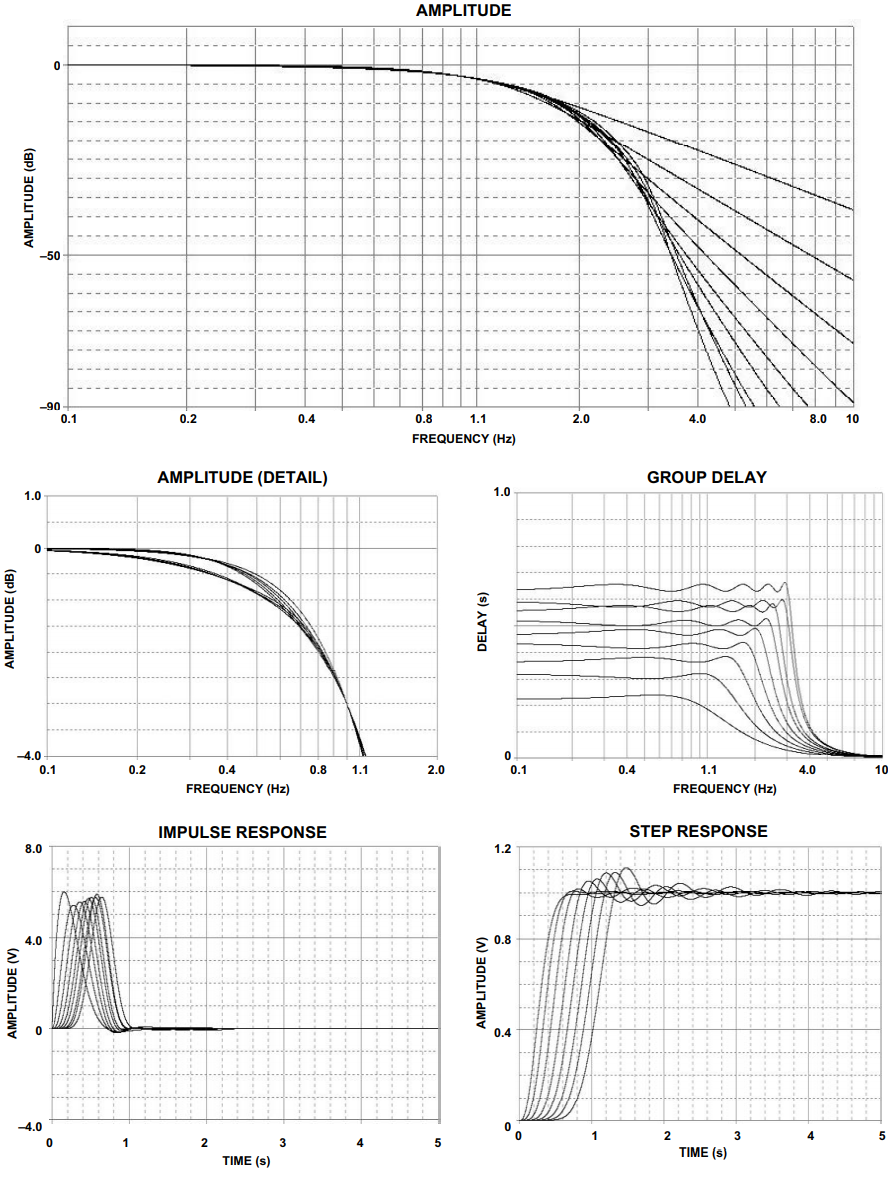
图9.线性相位，等纹误差为0.5°响应

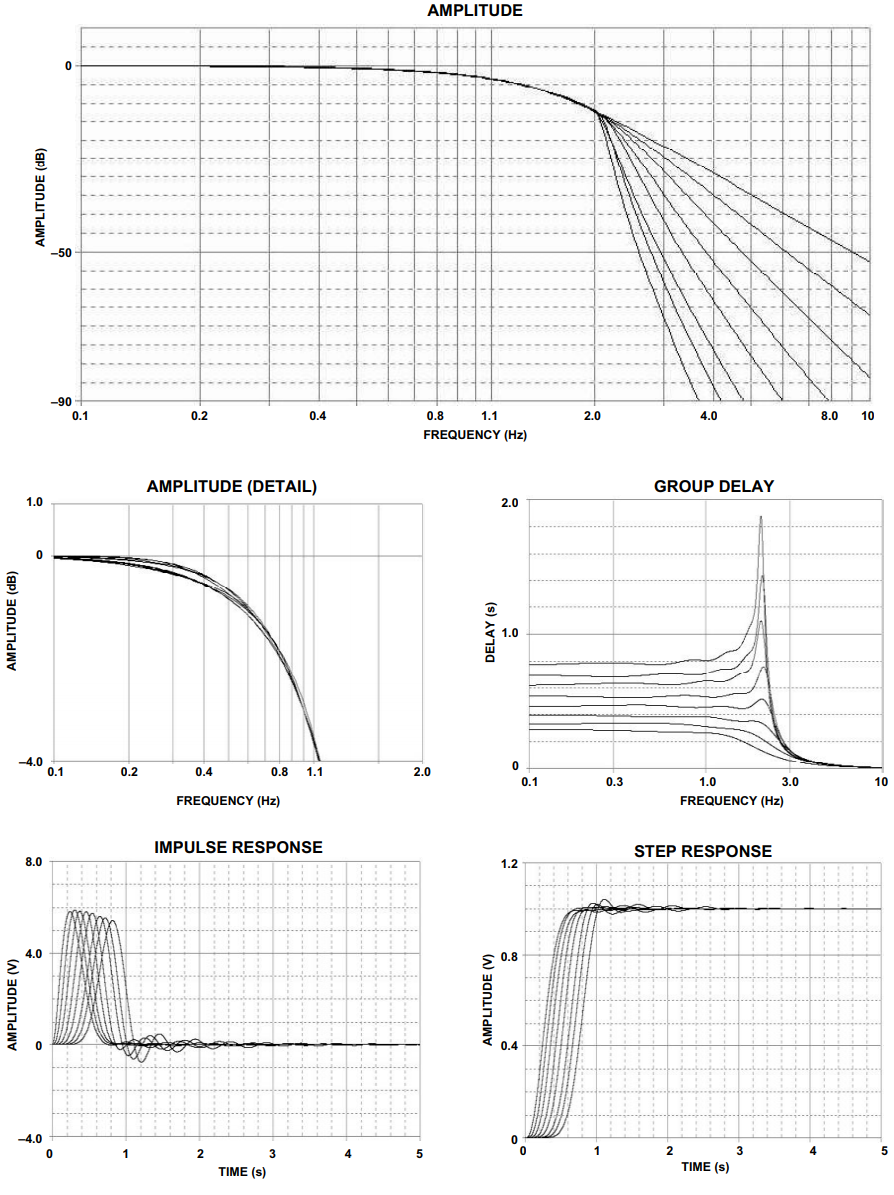
图 10.高斯至12 dB响应

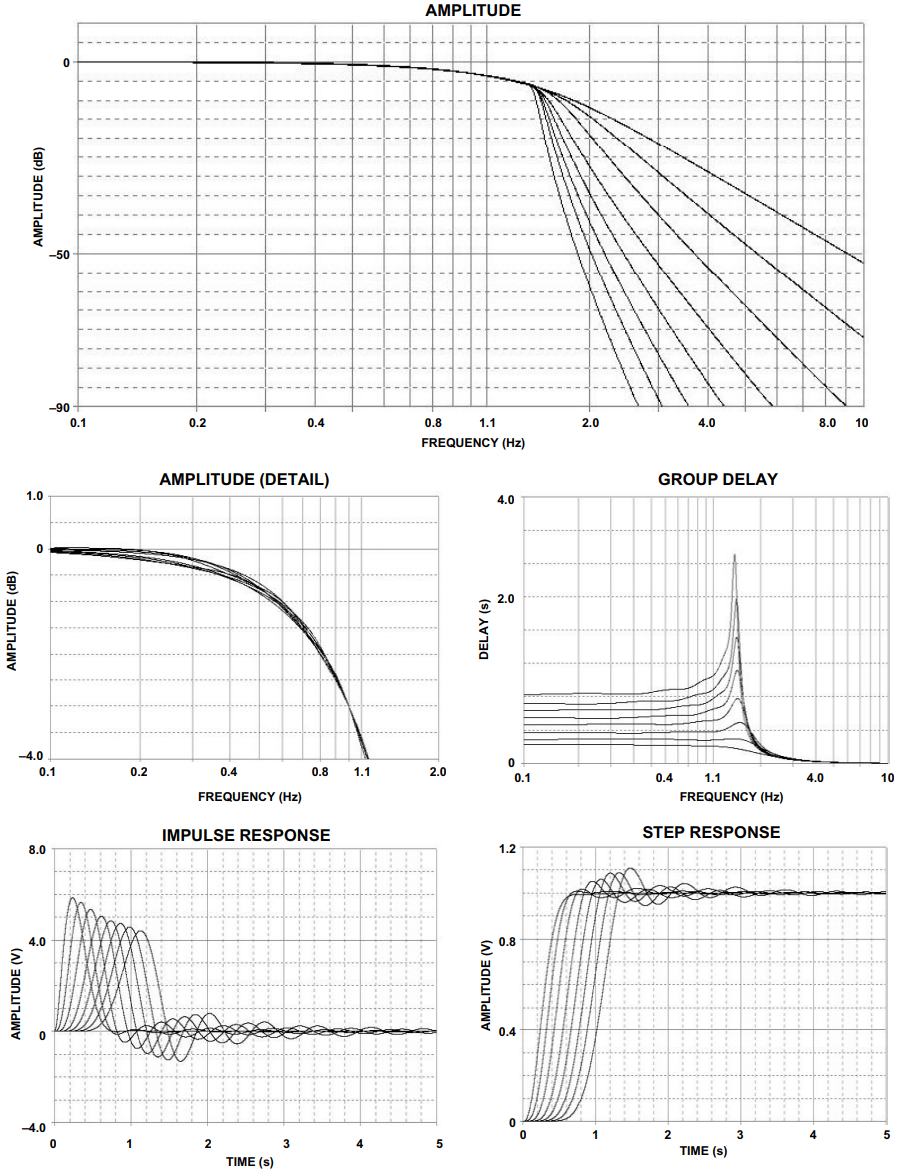
图 11.高斯至6 dB响应

 

次序	部分	真实部分	虚部	F0	α	Q	−3 dB 频率	峰值频率	峰值水平
2	1	0.7071	0.7071	1.0000	1.4142	0.7071	1.0000
3	1	0.5000	0.8660	1.0000	1.0000	1.0000		0.7071	1.2493
	2	1.0000		1.0000			1.0000
4	1	0.9239	0.3827	1.0000	1.8478	0.5412	0.7195
	2	0.3827	0.9239	1.0000	0.7654	1.3065		0.8409	3.0102
5	1	0.8090	0.5878	1.0000	1.6180	0.6180	0.8588
	2	0.3090	0.9511	1.0000	0.6180	1.6182		0.8995	4.6163
	3	1.0000		1.0000			1.0000
6	1	0.9659	0.2588	1.0000	1.9319	0.5176	0.6758
	2	0.7071	0.7071	1.0000	1.4142	0.7071	1.0000
	3	0.2588	0.9659	1.0000	0.5176	1.9319		0.9306	6.0210
7	1	0.9010	0.4339	1.0000	1.8019	0.5550	0.7449
	2	0.6235	0.7818	1.0000	1.2470	0.8019		0.4717	0.2204
	3	0.2225	0.9749	1.0000	0.4450	2.2471		0.9492	7.2530
	4	1.0000		1.0000			1.0000
8	1	0.9808	0.1951	1.0000	1.9616	0.5098	0.6615
	2	0.8315	0.5556	1.0000	1.6629	0.6013	0.8295
	3	0.5556	0.8315	1.0000	1.1112	0.9000		0.6186	0.6876
	4	0.1951	0.9808	1.0000	0.3902	2.5628		0.9612	8.3429
9	1	0.9397	0.3420	1.0000	1.8794	0.5321	0.7026
	2	0.7660	0.6428	1.0000	1.5320	0.6527	0.9172
	3	0.5000	0.8660	1.0000	1.0000	1.0000		0.7071	1.2493
	4	0.1737	0.9848	1.0000	0.3474	2.8785		0.9694	9.3165
	5	1.0000		1.0000			1.0000
10	1	0.9877	0.1564	1.0000	1.9754	0.5062	0.6549
	2	0.8910	0.4540	1.0000	1.7820	0.5612	0.7564
	3	0.7071	0.7071	1.0000	1.4142	0.7071	1.0000
	4	0.4540	0.8910	1.0000	0.9080	1.1013		0.7667	1.8407
	5	0.1564	0.9877	1.0000	0.3128	3.1970		0.9752	10.2023

次序	部分	真实部分	虚部	F0	α	Q	−3 dB 频率	峰值频率	峰值水平
2	1	0.6743	0.7075	0.9774	1.3798	0.7247		0.2142	0.0100
3	1	0.4233	0.8663	0.9642	0.8780	1.1389		0.7558	2.0595
	2	0.8467		0.8467			0.8467
4	1	0.6762	0.3828	0.7770	1.7405	0.5746	0.6069
	2	0.2801	0.9241	0.9656	0.5801	1.7237		0.8806	5.1110
5	1	0.5120	0.5879	0.7796	1.3135	0.7613		0.2889	0.0827
	2	0.1956	0.9512	0.9711	0.4028	2.4824		0.9309	8.0772
	3	0.6328		0.6328			0.6328
6	1	0.5335	0.2588	0.5930	1.7995	0.5557	0.4425
	2	0.3906	0.7072	0.8079	0.9670	1.0342		0.7204	3.4077
	3	0.1430	0.9660	0.9765	0.2929	3.4144		0.9689	10.7605
7	1	0.4393	0.4339	0.6175	1.4229	0.7028	0.6136
	2	0.3040	0.7819	0.8389	0.7247	1.3798		0.7204	3.4077
	3	0.1085	0.9750	0.9810	0.2212	4.5208		0.9689	13.1578
	4	0.4876		0.4876			0.4876
8	1	0.4268	0.1951	0.4693	1.8190	0.5498	0.3451
	2	0.3168	0.5556	0.6396	0.9907	1.0094		0.4564	1.3041
	3	0.2418	0.8315	0.8659	0.5585	1.7906		0.7956	5.4126
	4	0.0849	0.9808	0.9845	0.1725	5.7978		0.9771	15.2977
9	1	0.3686	0.3420	0.5028	1.4661	0.6821	0.4866
	2	0.3005	0.6428	0.7096	0.8470	1.1807		0.5682	2.3008
	3	0.1961	0.8661	0.8880	0.4417	2.2642		0.8436	7.3155
	4	0.0681	0.9848	0.9872	0.1380	7.2478		0.9824	17.2249
	5	0.3923		0.3923			0.3923
10	1	0.3522	0.1564	0.3854	1.8279	0.5471	0.2814
	2	0.3178	0.454	0.5542	1.1469	0.8719		0.3242	0.5412
	3	0.2522	0.7071	0.7507	0.6719	1.4884		0.6606	3.9742
	4	0.1619	0.891	0.9056	0.3576	2.7968		0.8762	9.0742
	5	0.0558	0.9877	0.9893	0.1128	8.8645		0.9861	18.9669

次序	部分	真实部分	虚部	F0	α	Q	−3 dB 频率	峰值频率	峰值水平
2	1	0.6104	0.7106	0.9368	1.3032	0.7673		0.3638	0.0999
3	1	0.3490	0.8684	0.9359	0.7458	1.3403		0.7952	3.1978
	2	0.6970		0.6970			0.6970
4	1	0.2177	0.9254	0.9507	0.4580	2.1834		0.8994	7.0167
	2	0.5257	0.3833	0.6506	1.6160	0.6188	0.5596
5	1	0.3842	0.5884	0.7027	1.0935	0.9145		0.4457	0.7662
	2	0.1468	0.9521	0.9634	0.3048	3.2812		0.9407	10.4226
	3	0.4749		0.4749			0.4749
6	1	0.3916	0.2590	0.4695	1.6682	0.5995	0.3879
	2	0.2867	0.7077	0.7636	0.7509	1.3316		0.6470	3.1478
	3	0.1049	0.9667	0.9724	0.2158	4.6348		0.9610	13.3714
7	1	0.3178	0.4341	0.5380	1.1814	0.8464		0.2957	0.4157
	2	0.2200	0.7823	0.8126	0.5414	1.8469		0.7507	5.6595
	3	0.0785	0.9755	0.9787	0.1604	6.2335		0.9723	15.9226
	4	0.3528		0.3528			0.3528
8	1	0.3058	0.1952	0.3628	1.6858	0.5932	0.2956
	2	0.2529	0.5558	0.6106	0.8283	1.2073		0.4949	2.4532
	3	0.1732	0.8319	0.8497	0.4077	2.4531		0.8137	7.9784
	4	0.0608	0.9812	0.9831	0.1237	8.0819		0.9793	18.1669
9	1	0.2622	0.3421	0.4310	1.2166	0.8219		0.2197	0.3037
	2	0.2137	0.6430	0.6776	0.6308	1.5854		0.6064	4.4576
	3	0.1395	0.8663	0.8775	0.3180	3.1450		0.8550	10.0636
	4	0.0485	0.9852	0.9864	0.0982	10.1795		0.9840	20.1650
	5	0.2790		0.2790			0.2790
10	1	0.2493	0.1564	0.2943	1.6942	0.5902	0.2382
	2	0.2249	0.4541	05067	0.8876	1.1266		0.3945	1.9880
	3	0.1785	0.7073	0.7295	0.4894	2.0434		0.6844	6.4750
	4	0.1146	0.8913	0.8986	0.2551	3.9208		0.8839	11.9386
	5	0.0395	0.9880	0.9888	0.0799	12.5163		0.9872	21.9565

次序	部分	真实部分	虚部	F0	α	Q	−3 dB 频率	峰值频率	峰值水平
2	1	0.5621	0.7154	0.9098	1.2356	0.8093		0.4425	0.2502
3	1	0.3062	0.8712	0.9234	0.6632	1.5079		0.8156	4.0734
	2	0.6124		0.6125			0.6124
4	1	0.4501	0.3840	0.5916	1.5215	0.6572	0.5470
	2	0.1865	0.9272	0.9458	0.3944	2.5356		0.9082	8.2538
5	1	0.3247	0.5892	0.6727	0.9653	1.0359		0.4917	1.4585
	2	0.1240	0.9533	0.9613	0.2580	3.8763		0.9452	11.8413
	3	0.4013		0.4013			0.4013
6	1	0.3284	0.2593	0.4184	1.5697	0.6371	0.3730
	2	0.2404	0.7083	0.7480	0.6428	1.5557		0.6663	4.3121
	3	0.0880	0.9675	0.9715	0.1811	5.5205		0.9635	14.8753
7	1	0.2652	0.4344	0.5090	1.0421	0.9596		0.3441	1.0173
	2	0.1835	0.7828	0.8040	0.4565	2.1908		0.7610	7.0443
	3	0.0655	0.9761	0.9783	0.1339	7.4679		0.9739	17.4835
	4	0.2944		0.2944			0.2944
8	1	0.2543	0.1953	0.3206	1.5862	0.6304	0.2822
	2	0.2156	0.5561	0.5964	0.7230	1.3832		0.5126	3.4258
	3	0.1441	0.8323	0.8447	0.3412	2.9309		0.8197	9.4683
	4	0.0506	0.9817	0.9830	0.1029	9.7173		0.9804	19.7624
9	1	0.2176	0.3423	0.4056	1.0730	0.9320		0.2642	0.8624
	2	0.1774	0.6433	0.6673	0.5317	1.8808		0.6184	5.8052
	3	0.1158	0.8667	0.8744	0.2649	3.7755		0.8589	11.6163
	4	0.0402	0.9856	0.9864	0.0815	12.2659		0.9848	21.7812
	5	0.2315		0.2315			0.2315
10	1	0.2065	0.1565	0.2591	1.5940	0.6274	0.2267
	2	0.1863	0.4543	0.4910	0.7588	1.3178		0.4143	3.0721
	3	0.1478	0.7075	0.7228	0.4090	2.4451		0.6919	7.9515
	4	0.0949	0.8915	0.8965	0.2117	4.7236		0.8864	13.5344
	5	0.0327	0.9883	0.9888	0.0661	15.1199		0.9878	23.5957

次序	部分	真实部分	虚部	F0	α	Q	−3 dB 频率	峰值频率	峰值水平
2	1	0.5129	0.7225	1.2314	1.1577	0.8638		0.7072	0.5002
3	1	0.2683	0.8753	1.0688	0.5861	1.7061		0.9727	5.0301
	2	0.5366		0.6255			0.6265
4	1	0.3872	0.3850	0.5969	1.4182	0.7051	0.5951
	2	0.1605	0.9297	1.0313	0.3402	2.9391		1.0010	9.4918
5	1	0.2767	0.5902	0.6905	0.8490	1.1779		0.5522	2.2849
	2	0.1057	0.9550	1.0178	0.2200	4.5451		1.0054	13.2037
	3	0.3420		0.3623			0.3623
6	1	0.2784	0.2596	0.3963	1.4627	0.6836	0.3827
	2	0.2037	0.7091	0.7680	0.5522	1.8109		0.7071	5.5025
	3	0.0746	0.9687	1.0114	0.1536	6.5119		1.0055	16.2998
7	1	0.2241	0.4349	0.5040	0.9161	1.0916		0.3839	1.7838
	2	0.1550	0.7836	0.8228	0.3881	2.5767		0.7912	8.3880
	3	0.0553	0.9771	1.0081	0.1130	8.8487		1.0049	18.9515
	4	0.2487		0.2562			0.2562
8	1	0.2144	0.1955	0.2968	1.4779	0.6767	0.2835
	2	0.1817	0.5565	0.5989	0.6208	1.6109		0.5381	4.5815
	3	0.1214	0.8328	0.8610	0.2885	3.4662		0.8429	10.8885
	4	0.0426	0.9824	1.0060	0.0867	11.5305		1.0041	21.2452
9	1	0.1831	0.3425	0.3954	0.9429	1.0605		0.2947	1.6023
	2	0.1493	0.6436	0.6727	0.4520	2.2126		0.6374	7.1258
	3	0.0974	0.8671	0.8884	0.2233	4.4779		0.8773	13.0759
	4	0.0338	0.9861	1.0046	0.0686	14.5829		1.0034	23.2820
	5	0.1949		0.1984			0.1984
10	1	0.1736	0.1566	0.2338	1.4851	0.6734	0.2221
	2	0.1566	0.4545	0.4807	0.6515	1.5349		0.4267	4.2087
	3	0.1243	0.7078	0.7186	0.3459	2.8907		0.6968	9.3520
	4	0.0798	0.8919	0.8955	0.1782	5.6107		0.8883	15.0149
	5	0.0275	0.9887	0.9891	0.0556	17.9833		0.9883	25.1008

次序	部分	真实部分	虚部	F0	α	Q	−3 dB 频率	峰值频率	峰值水平
2	1	0.4508	0.7351	0.8623	1.0456	0.9564		0.5806	0.9995
3	1	0.2257	0.8822	0.9106	0.4957	2.0173		0.8528	6.3708
	2	0.4513		0.4513			0.4513
4	1	0.3199	0.3868	0.5019	1.2746	0.7845		0.2174	0.1557
	2	0.1325	0.9339	0.9433	0.2809	3.5594		0.9245	11.1142
5	1	0.2265	0.5918	0.6337	0.7149	1.3988		0.5467	3.5089
	2	0.0865	0.9575	0.9614	0.1800	5.5559		0.9536	14.9305
	3	0.2800		0.2800			0.2800
6	1	0.2268	0.2601	0.3451	1.3144	0.7608		0.1273	0.0813
	2	0.1550	0.7106	0.7273	0.4262	2.3462		0.6935	7.6090
	3	0.0608	0.9707	0.9726	0.1249	8.0036		0.9688	18.0827
7	1	0.1819	0.4354	0.4719	0.7710	1.2971		0.3956	2.9579
	2	0.1259	0.7846	0.7946	0.3169	3.1558		0.7744	10.0927
	3	0.0449	0.9785	0.9795	0.0918	10.8982		0.9775	20.7563
	4	0.2019		0.2019			0.2019
8	1	0.1737	0.1956	0.2616	1.3280	0.7530		0.0899	0.0611
	2	0.1473	0.5571	0.5762	0.5112	1.9560		0.5373	6.1210
	3	0.0984	0.8337	0.8395	0.2344	4.2657		0.8279	12.6599
	4	0.0346	0.9836	0.9842	0.0702	14.2391		0.9830	23.0750
9	1	0.1482	0.3427	0.3734	0.7938	1.2597		0.3090	2.7498
	2	0.1208	0.6442	0.6554	0.3686	2.7129		0.6328	8.8187
	3	0.0788	0.8679	0.8715	0.1809	5.5268		0.8643	14.8852
	4	0.0274	0.9869	0.9873	0.0555	18.0226		0.9865	25.1197
	5	0.1577		0.1577			0.1577
10	1	0.1403	0.1567	0.2103	1.3341	0.7496		0.0698	0.0530
	2	0.1266	0.4548	0.4721	0.5363	1.8645		0.4368	5.7354
	3	0.1005	0.7084	0.7155	0.2809	3.5597		0.7012	11.1147
	4	0.0645	0.8926	0.8949	0.1441	6.9374		0.8903	16.8466
	5	0.0222	0.9895	0.9897	0.0449	22.2916		0.9893	26.9650

次序	部分	真实部分	虚部	F0	α	Q	−3 dB 频率	峰值频率	峰值水平
2	1	1.1050	0.6368	1.2754	1.7328	0.5771	1.0020
3	1	1.0509	1.0025	1.4524	1.4471	0.6910	1.4185
	2	1.3270		1.3270			1.3270
4	1	1.3596	0.4071	1.4192	1.9160	0.5219	0.9705
	2	0.9877	1.2476	1.5912	1.2414	0.8055		0.7622	0.2349
5	1	1.3851	0.7201	1.5611	1.7745	0.5635	1.1876
	2	0.9606	1.4756	1.7607	1.0911	0.9165		1.1201	0.7768
	3	1.5069		1.5069			1.5069
6	1	1.5735	0.3213	1.6060	1.9596	0.5103	1.0638
	2	1.3836	0.9727	1.6913	1.6361	0.6112	1.4323
	3	0.9318	1.6640	1.9071	0.9772	1.0234		1.3786	1.3851
7	1	1.6130	0.5896	1.7174	1.8784	0.5324	1.2074
	2	1.3797	1.1923	1.8235	1.5132	0.6608	1.6964
	3	0.9104	1.8375	2.0507	0.8879	1.1262		1.5961	1.9860
	4	1.6853		1.6853			1.6853
8	1	1.7627	0.2737	1.7838	1.9763	0.5060	1.1675
	2	0.8955	2.0044	2.1953	0.8158	1.2258		1.7932	2.5585
	3	1.3780	1.3926	1.9591	1.4067	0.7109		0.2011	0.0005
	4	1.6419	0.8256	1.8378	1.7868	0.5597	1.3849
9	1	1.8081	0.5126	1.8794	1.9242	0.5197	1.2774
	2	1.6532	1.0319	1.9488	1.6966	0.5894	1.5747
	3	1.3683	1.5685	2.0815	1.3148	0.7606		0.7668	0.0807
	4	0.8788	2.1509	2.3235	0.7564	1.3220		1.9632	3.0949
	5	1.8575		1.8575			1.8575
10	1	1.9335	0.2451	1.9490	1.9841	0.5040	1.2685
	2	1.8467	0.7335	1.9870	1.8587	0.5380	1.4177
	3	1.6661	1.2246	2.0678	1.6115	0.6205	1.7848
	4	1.3648	1.7395	2.2110	1.2346	0.8100		1.0785	0.2531
	5	0.8686	2.2294	2.4580	0.7067	1.4150		2.1291	3.5944

次序	部分	真实部分	虚部	F0	α	Q	−3 dB 频率	峰值频率	峰值水平
2	1	1.0087	0.6680	1.2098	1.6675	0.5997	0.9999
3	1	0.8541	1.0725	1.3710	1.2459	0.8026		0.6487	0.2232
	2	1.0459		1.0459			1.0459
4	1	0.9648	0.4748	1.0753	1.7945	0.5573	0.8056
	2	0.7448	1.4008	1.5865	0.9389	1.0650		1.1864	1.6286
5	1	0.8915	0.8733	1.2480	1.4287	0.6999	1.2351
	2	0.6731	1.7085	1.8363	0.7331	1.3641		1.5703	3.3234
	3	0.9430		0.9430			0.9430
6	1	0.8904	0.4111	0.9807	1.8158	0.5507	0.7229
	2	0.8233	1.2179	1.4701	1.1201	0.8928		0.8975	0.6495
	3	0.6152	1.9810	2.0743	0.5932	1.6859		1.8831	4.9365
7	1	0.8425	0.7791	1.1475	1.4684	0.6810	1.1036
	2	0.7708	1.5351	1.7177	0.8975	1.1143		1.3276	1.9162
	3	0.5727	2.2456	2.3175	0.4942	2.0233		2.1713	6.3948
	4	0.8615		0.8615			0.8615
8	1	0.8195	0.3711	0.8996	1.8219	0.5489	0.6600
	2	0.7930	1.1054	1.3604	1.1658	0.8578		0.7701	0.4705
	3	0.7213	1.8134	1.9516	0.7392	1.3528		1.6638	3.2627
	4	0.5341	2.4761	2.5330	0.4217	2.3713		2.4178	7.6973
9	1	0.7853	0.7125	1.0604	1.4812	0.6751	1.0102
	2	0.7555	1.4127	1.6020	0.9432	1.0602		1.1937	1.6005
	3	0.6849	2.0854	2.1950	0.6241	1.6024		1.9667	4.5404
	4	0.5060	2.7133	2.7601	0.3667	2.7274		2.6657	8.8633
	5	0.7983		0.7983			0.7983
10	1	0.7592	0.3413	0.8324	1.8241	0.5482	0.6096
	2	0.7467	1.0195	1.2637	1.1818	0.8462		0.6941	0.4145
	3	0.7159	1.6836	1.8295	0.7826	1.2778		1.5238	2.8507
	4	0.6475	2.3198	2.4085	0.5377	1.8598		2.2276	5.7152
	5	0.4777	2.9128	2.9517	0.3237	3.0895		2.8734	9.9130

Order	Section	Real Part	Imaginary Part	F0	α	Q	−3 dB Frequency	Peaking Frequency	Peaking Level
2	1	0.8590	0.6981	1.1069	1.5521	0.6443	1.000
3	1	0.6969	1.1318	1.3292	1.0486	0.9536		0.8918	0.9836
	2	0.8257		0.8257			0.8257
4	1	0.7448	0.5133	0.9045	1.6468	0.6072	0.7597
	2	0.6037	1.4983	1.6154	0.7475	1.3379		1.3713	3.1817
5	1	0.6675	0.9401	1.1588	1.1693	0.8552		0.6518	0.4579
	2	0.5412	1.8256	1.9041	0.5684	1.7592		1.7435	5.2720
	3	0.7056		0.7056			0.7056
6	1	0.6519	0.4374	0.7850	1.6608	0.6021	0.6522
	2	0.6167	1.2963	1.4355	0.8592	1.1639		1.1402	2.2042
	3	0.4893	2.0982	2.1545	0.4542	2.2016		2.0404	7.0846
7	1	0.6190	0.8338	1.0385	1.1922	0.8388		0.5586	0.3798
	2	0.5816	1.6455	1.7453	0.6665	1.5004		1.5393	4.0353
	3	0.4598	2.3994	2.4431	0.3764	2.6567		2.3549	8.6433
	4	0.6283			0.6283		0.6283
8	1	0.5791	0.3857	0.6958	1.6646	0.6007	0.5764
	2	0.5665	1.1505	1.2824	0.8835	1.1319		1.0014	2.0187
	3	0.5303	1.8914	1.9643	0.5399	1.8521		1.8155	5.6819
	4	0.4148	2.5780	2.6112	0.3177	3.1475		2.5444	10.0703
9	1	0.5688	0.7595	0.9489	1.1989	0.8341		0.5033	0.3581
	2	0.5545	1.5089	1.6076	0.6899	1.4496		1.4033	3.7748
	3	0.5179	2.2329	2.2922	0.4519	2.2130		2.1720	7.1270
	4	0.4080	2.9028	2.9313	0.2784	3.5923		2.8740	11.1925
	5	0.5728		0.5728			0.5728
10	1	0.5249	0.3487	0.6302	1.6659	0.6003	0.5215
	2	0.5193	1.0429	1.1650	0.8915	1.1217		0.9044	1.9598
	3	0.5051	1.7264	1.7988	0.5616	1.7806		1.6509	5.3681
	4	0.4711	2.3850	2.4311	0.3876	2.5802		2.3380	8.3994
	5	0.3708	2.9940	3.0169	0.2458	4.0681		2.9709	12.2439

Order	Section	Real Part	Imaginary Part	F0	α	Q	−3 dB Frequency	Peaking Frequency	Peaking Level
3	1	0.9622	1.2214	1.5549	1.2377	0.8080		0.7523	0.2448
	2	0.9776	0.5029	1.0994	1.7785	0.5623	0.8338
4	1	0.7940	0.5029	0.9399	1.6896	0.5919	0.7636
	2	0.6304	1.5407	1.6647	0.7574	1.3203		1.4058	3.0859
5	1	0.6190	0.8254	1.0317	1.1999	0.8334		0.5460	0.3548
	2	0.3559	1.5688	1.6087	0.4425	2.2600		1.5279	7.3001
	3	0.6650		0.6650			0.6650
6	1	0.5433	0.3431	0.6426	1.6910	0.5914	0.5215
	2	0.4672	0.9991	1.1029	0.8472	1.1804		0.8831	2.2992
	3	0.2204	1.5067	1.5227	0.2895	3.4545		1.4905	10.8596
7	1	0.4580	0.5932	0.7494	1.2223	0.8182		0.3770	0.2874
	2	0.3649	1.1286	1.1861	0.6153	1.6253		1.0680	4.6503
	3	0.1522	1.4938	1.5015	0.2027	4.9328		1.4860	13.9067
	4	0.4828		0.4828		0.4828
8	1	0.4222	0.2640	0.4979	1.6958	0.5897	0.4026
	2	0.3833	0.7716	0.8616	0.8898	1.1239		0.6697	1.9722
	3	0.2678	1.2066	1.2360	0.4333	2.3076		1.1765	7.4721
	4	0.1122	1.4798	1.4840	0.1512	6.6134		1.4755	16.4334
9	1	0.3700	0.4704	0.5985	1.2365	0.8088		0.2905	0.2480
	2	0.3230	0.9068	0.9626	0.6711	1.4901		0.8473	3.9831
	3	0.2309	1.2634	1.2843	0.3596	2.7811		1.2421	9.0271
	4	0.0860	1.4740	1.4765	0.1165	8.5804		1.4715	18.6849
	5	0.3842		0.3842			0.3842
10	1	0.3384	0.2101	0.3983	1.6991	0.5885	0.3212
	2	0.3164	0.6180	0.6943	0.9114	1.0972		0.5309	1.8164
	3	0.2677	0.9852	1.0209	0.5244	1.9068		0.9481	5.9157
	4	0.1848	1.2745	1.2878	0.2871	3.4825		1.2610	10.9284
	5	0.0671	1.4389	1.4405	0.0931	10.7401		1.4373	20.6296

Order	Section	Real Part	Imaginary Part	F0	α	Q	−3 dB Frequency	Peaking Frequency	Peaking Level
3	1	0.9360	1.2168	1.5352	1.2194	0.8201		0.7775	0.2956
	2	0.9360		0.9360			0.9360
4	1	0.9278	1.6995	1.9363	0.9583	1.0435		1.4239	1.5025
	2	0.9192	0.5560	1.0743	1.7113	0.5844	0.8582
5	1	0.8075	0.9973	1.2832	1.2585	0.7946		0.5853	0.1921
	2	0.7153	0.2053	0.7442	1.9224	0.5202	0.5065
	3	0.8131		0.8131			0.8131
6	1	0.7019	0.4322	0.8243	1.7030	0.5872	0.6627
	2	0.6667	1.2931	1.4549	0.9165	1.0911		1.1080	1.7809
	3	0.4479	2.1363	2.1827	0.4104	2.4366		2.0888	7.9227
7	1	0.6155	0.7703	0.9860	1.2485	0.8010		0.4632	0.2168
	2	0.5486	1.5154	1.6116	0.6808	1.4689		1.4126	3.8745
	3	0.2905	2.1486	2.1681	0.2680	3.7318		2.1289	11.5169
	4	0.6291		0.6291			0.6291
8	1	0.5441	0.3358	0.6394	1.7020	0.5876	0.5145
	2	0.5175	0.9962	1.1226	0.9220	1.0846		0.8512	1.7432
	3	0.4328	1.6100	1.6672	0.5192	1.9260		1.5507	5.9962
	4	0.1978	2.0703	2.0797	0.1902	5.2571		2.0608	14.4545
9	1	0.4961	0.6192	0.7934	1.2505	0.7997		0.3705	0.2116
	2	0.4568	1.2145	1.2976	0.7041	1.4203		1.1253	3.6221
	3	0.3592	1.7429	1.7795	0.4037	2.4771		1.7055	8.0594
	4	0.1489	2.1003	2.1056	0.1414	7.0704		2.0950	17.0107
	5	0.5065		0.5065			0.5065
10	1	0.4535	0.2794	0.5327	1.7028	0.5873	0.4283
	2	0.4352	0.8289	0.9362	0.9297	1.0756		0.7055	1.6904
	3	0.3886	1.3448	1.3998	0.5552	1.8011		1.2874	5.4591
	4	0.2908	1.7837	1.8072	0.3218	3.1074		1.7598	9.9618
	5	0.1136	2.0599	2.0630	0.1101	9.0802		2.0568	19.1751

 

比较响应

现在将比较几个全极点滤波器的响应，即贝塞尔、巴特沃斯和切比雪夫（在本例中为0.5 dB纹波）。使用8极点滤波器作为比较的基础。响应已归一化，截止频率为 1 Hz。 比较图 12 和图 13，很容易看出各种响应的权衡取舍。从贝塞尔到北海再到切比雪夫，人们可以看到，随着瞬态行为逐渐变差，振幅判别力有所改善。

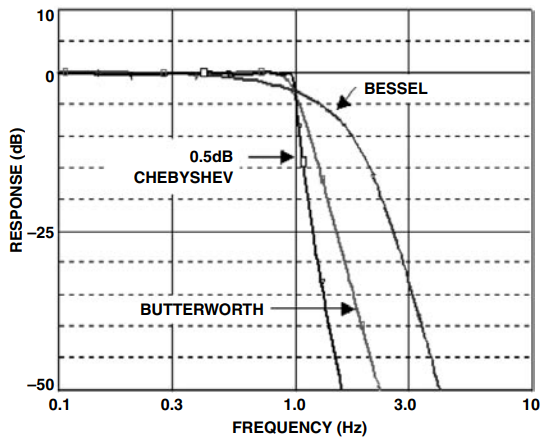
图 12.幅度响应比较

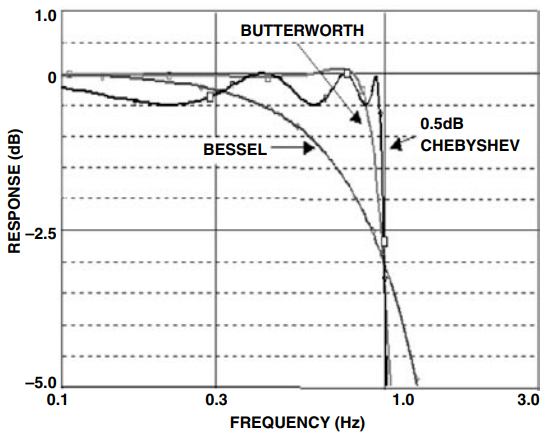
图 13.幅度响应比较（详细信息）

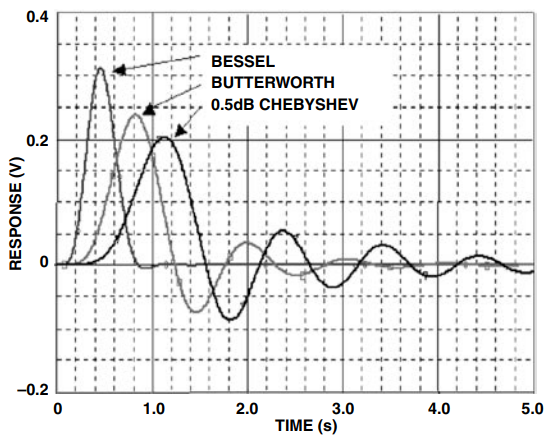
图 14.脉冲响应比较

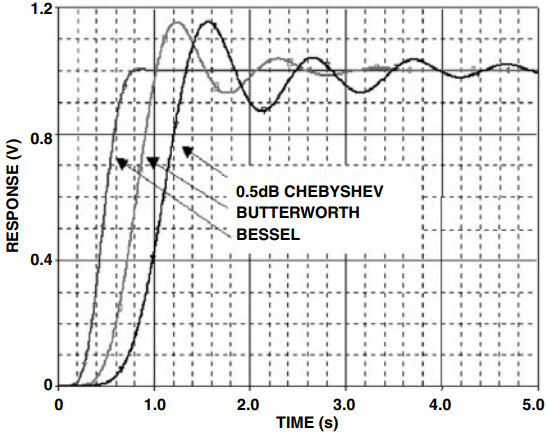
图 15.阶跃响应比较

过滤器拓扑

既然已经决定了要构建什么，现在必须决定如何构建它。这意味着有必要决定使用哪种滤波器拓扑。滤波器设计是一个两步过程，其中确定要构建的内容（滤波器传递函数），然后确定如何构建它（用于电路的拓扑）。通常，滤波器由实极的 1 极部分和极对的 3 极部分构成。虽然可以从<>极点或更高阶的截面中构建滤波器，但部分中组件之间的相互作用会增加，因此组件灵敏度也会增加。最好使用缓冲区来隔离各个部分。此外，假设所有滤波器部分均由低阻抗源驱动。任何源阻抗都可以建模为与滤波器输入串联。

在所有设计方程图中，将使用以下约定：

H = 通带或谐振时的电路增益

FC= 截止或谐振频率（以 Hz 为单位）

ω0= 截止或谐振频率，单位为弧度/秒

Q = 电路“品质因数”;指示电路峰值

α = 1/Q = 阻尼比

不幸的是，符号α用于阻尼比。它与用于表示极点位置的α不同（α ± jβ）。Q 也会出现同样的问题。它用于电路质量因数和元件质量因数，它们不是一回事。电路Q是电路中的峰值量。这是极点与 s 平面中原点的角度的函数。分量Q是无损电抗中的损耗数。这些损耗是元件的寄生效应——耗散因数、漏电阻、ESR（等效串联电阻）等。在电容器和串联电阻和电感器中的寄生电容。

萨伦键滤波器

Sallen-Key配置，也称为电压控制电压源（VCVS），由麻省理工学院林肯实验室的R.P. Sallen和E.L. Key于1955年首次推出。它是使用最广泛的滤波器拓扑之一。这种受欢迎的一个原因是，这种配置显示滤波器性能对运算放大器性能的依赖性最小。这是因为运算放大器不是配置为积分器，而是配置为放大器，从而最大限度地降低了其增益带宽要求。由此推断，由于运算放大器增益带宽积不会像配置为积分器那样限制滤波器的性能，因此可以设计出比其他拓扑结构更高的频率滤波器。保持通过滤波器的信号相位（同相配置）。这种配置的另一个优点是最大电阻值与最小电阻值的比率以及最大电容器值与最小电容器值的比率（元件分布）较低，有利于可制造性。频率和Q项有些独立，但它们对增益参数非常敏感。SallenKey对元素值非常敏感，特别是对于高Q值部分。Sallen-Key低通滤波器的设计公式如图16所示。

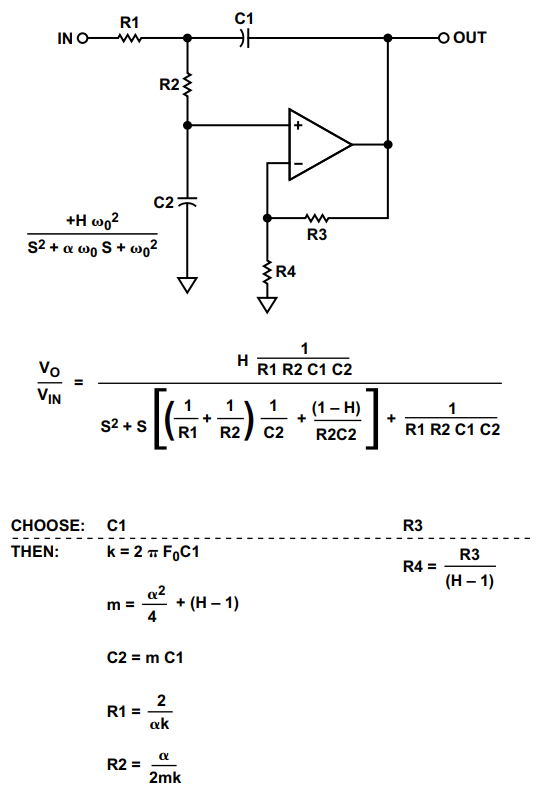
图 16.萨伦键低通设计方程

二阶Sallen-Key低通滤波器有一个特例。如果增益设置为2，则电容值和电阻值将相同。

虽然Sallen-Key滤波器被广泛使用，但一个严重的缺点是滤波器不容易调谐，因为F上的分量值相互作用0和问。

Sallen-Key高通滤波器的设计公式如图17所示。

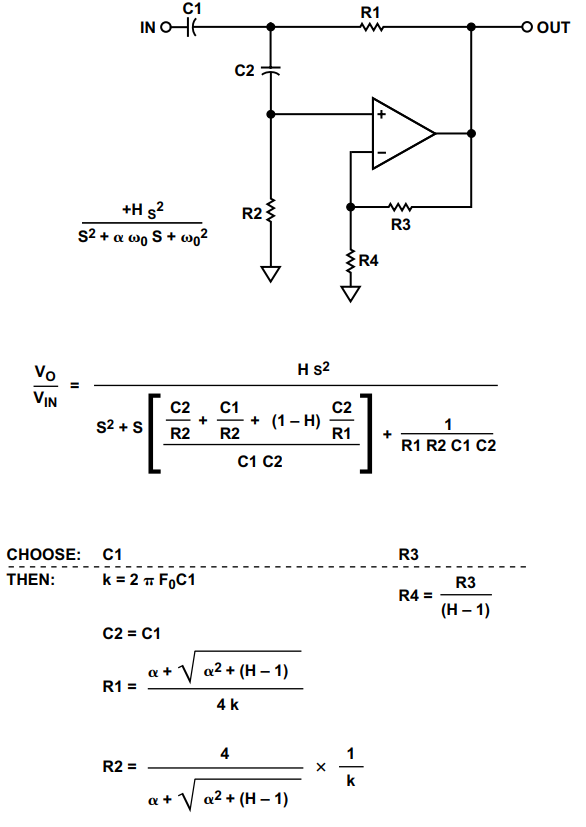
图 17.萨伦键高通设计方程

Sallen-Key滤波器的带通情况有一个限制。Q的值将决定滤波器的增益，即它不能像低通或高通情况下那样独立设置。Sallen-Key带通的设计公式如图18所示。

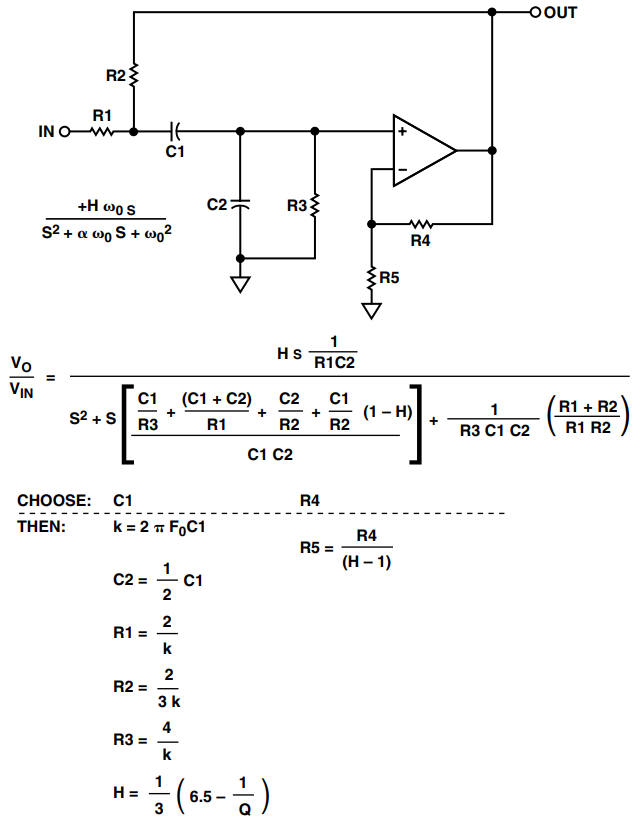
图 18.萨伦键带通设计公式

多反馈滤波器

多反馈滤波器使用运算放大器作为积分器。因此，传递函数对运算放大器参数的依赖性大于Sallen-Key实现。由于运算放大器开环增益的限制，很难产生高Q、高频部分。运算放大器的开环增益应至少比谐振（或截止）频率下的幅度响应高20 dB（×10），包括滤波器Q引起的峰值。Q引起的峰值将导致幅度A0:

其中H是电路的增益。多重反馈滤波器将反转信号的相位。这相当于将产生的180°相移添加到滤波器本身的相移中。

多重反馈情况下的最大与最小元件值比高于Sallen-Key实现。多反馈低通滤波器的设计公式如图19所示。

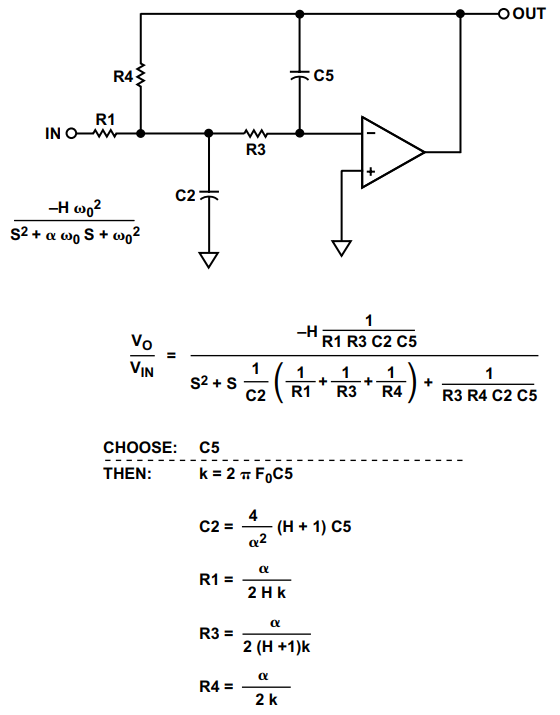
图 19.多反馈低通设计公式

多反馈高通滤波器的设计公式如图20所示。

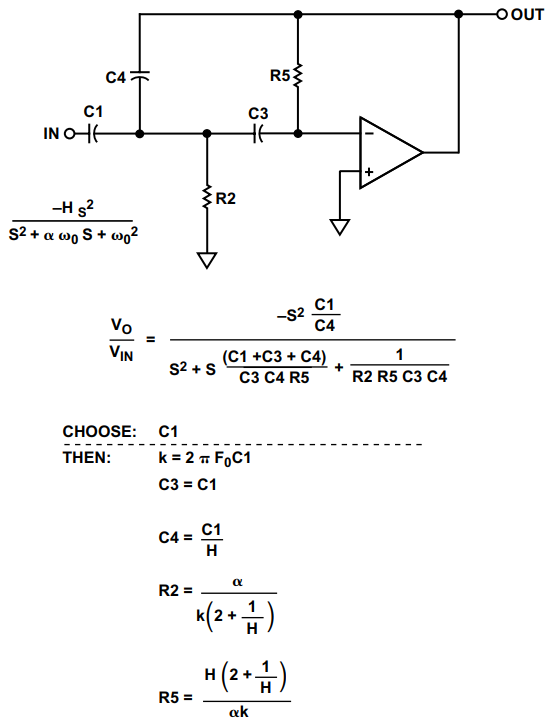
图 20.多反馈高通设计公式

多反馈带通情况的设计公式如图21所示。该电路广泛用于低Q值（<20）应用。它允许对谐振频率F进行一些调谐0，通过使 R2 可变。Q 也可以调整（使用 R5），但这也会改变 F0.F 的调谐0可以通过用示波器的水平通道监控滤波器的输出来实现，滤波器的输入连接到垂直通道。显示将是一个李萨如图案，由一个椭圆组成，该椭圆在共振时将坍缩成一条直线，因为相移将是 180°。还可以调整输出以获得最大输出，这也将在共振时发生;这通常不那么精确，特别是在Q值较低时，峰值不太明显。

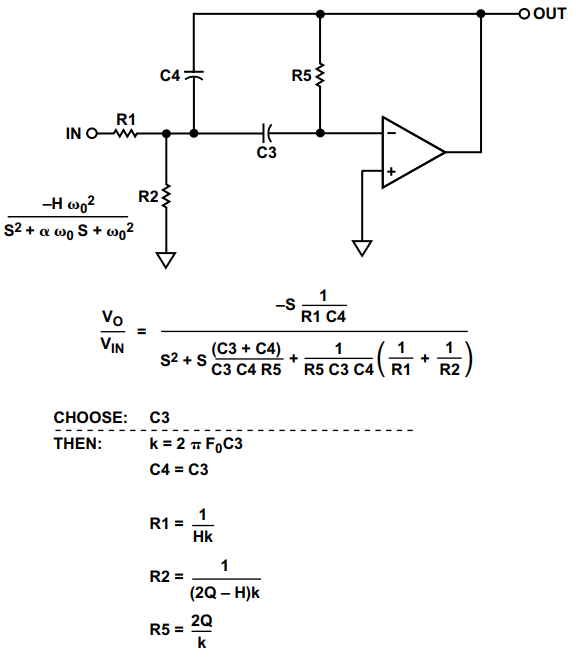
图 21.多反馈带通设计公式

状态变量筛选器

状态变量的实现提供了最精确的实现，但牺牲了更多的电路元件。所有三个主要参数（增益、Q和ω0） 可以独立调整，同时提供低通、高通和带通输出。请注意，低通和高通输出同相反相，而带通输出保持相位。滤波器每个输出的增益也是独立可变的。

由于状态变量滤波器的所有参数都可以独立调整，因此可以最大限度地减少分量扩散。此外，由于温度和组件公差引起的变化被最小化。积分器部分使用的运算放大器对运算放大器增益带宽的限制与多反馈部分所述相同。

状态变量滤波器的设计公式如图22所示。

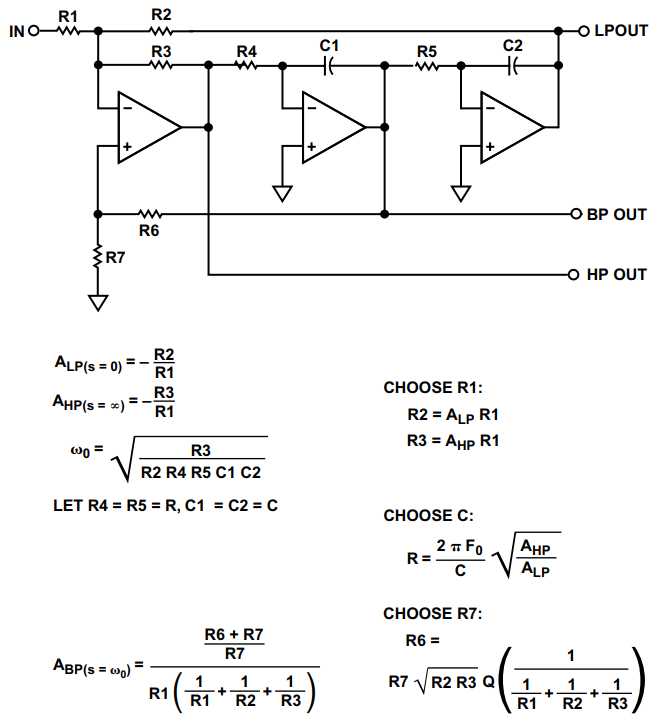
图 22.状态变量设计方程

调谐状态变量滤波器的谐振频率是通过改变R4和R5来实现的。虽然两者都不必调谐，但如果在很宽的范围内变化，通常更可取。保持R1恒定，调谐R2设置低通增益，调谐R3设置高通增益。带通增益和Q由R6和R7之比设置。

由于状态变量滤波器的参数是独立且可调的，因此很容易添加频率、Q 和 ω 的电子控制0.这种调整通过使用乘法DAC（MDAC）或数字电位计来完成。对于积分器部分，添加MDAC通过分压驱动电阻器来有效地增加时间常数，从而为积分器电容器提供充电电流。实际上，这提高了电阻，进而提高了时间常数。Q和增益可以通过改变各种反馈路径的比率来改变。数字电位计将通过直接改变电阻值，以更直接的方式完成相同的壮举。由此产生的可调谐滤波器在测量和控制电路中提供了很大的实用性。

双二次（双二阶）滤波器

状态变量滤波器的近亲是双二体。该电路的名称由J. Tow于1968年首次使用，后来由L.C. Thomas于1971年使用，其来源于传递函数在分子和分母中都是二次的事实。因此，传递函数是双二次函数。该电路是对状态变量电路的轻微重新排列。一个显著的区别是没有单独的高通输出。带通输出反相。有两个低通输出，一个同相，一个异相。通过增加第四个放大器部分，可以实现高通滤波器。双二阶图的设计公式如图23所示。

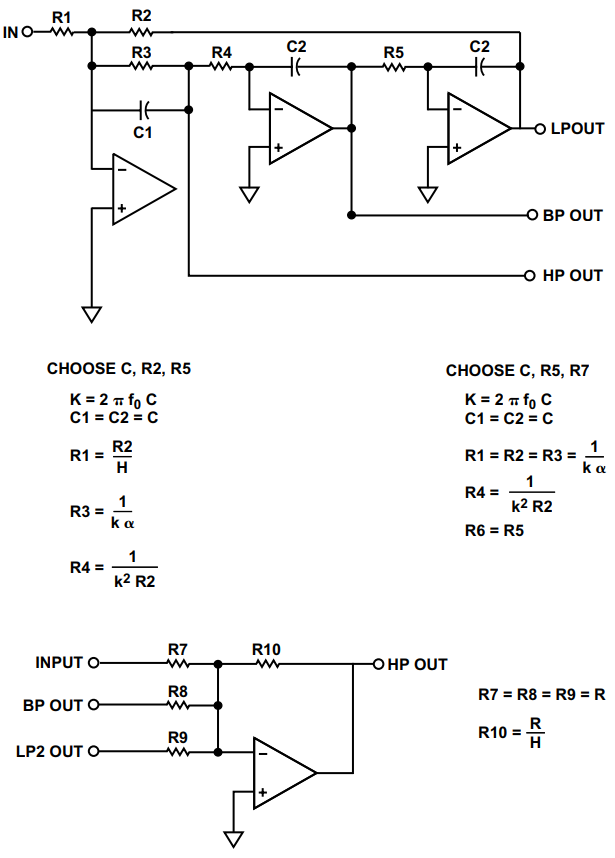
图 23.双二阶设计方程

参考图23，输入、带通和第二低通输出相加，用于高通输出。在这种情况下，约束是 R1 = R2 = R3 和 R7 = R8 = R9。

与状态变量一样，双二阶滤波器也是可调的。调整R3将调整Q.调整R4将设置谐振频率。调整R1将设置增益。频率通常先调整，然后调整Q，然后调整增益。以这种方式设置参数可最大程度地减少组件值交互的影响。

运算放大器要求

为原型响应生成的曲线是使用理想的运算放大器完成的。实际上，运算放大器是一个单极点低通滤波器。放大器的主极点是滤波器的转折频率。运算放大器的传递函数将添加到滤波器响应中。

实际上，这意味着如果运算放大器的增益带宽积不比滤波器的截止频率至少大一个数量级，就会有一些相互作用。如果放大器的增益带宽积比滤波器高一个数量级以上，则运算放大器的响应通常可以忽略不计。在任何情况下，如果有顾虑，可以下载滤波器SPICE卡座，并使用SPICE模拟将使用的特定运算放大器的SPICE模型。

电流反馈放大器只能与Sallen-Key拓扑一起使用，因为这是唯一将运算放大器配置为放大器的拓扑。在其他拓扑中，运算放大器与反馈网络中的电容一起使用，这不适合电流反馈放大器。

另一种选择是双极性或FET输入器件。通常，如果滤波器的阻抗电平小于1 kΩ，则双极性运算放大器是合适的选择。如果阻抗大于10 kΩ，FET输入运算放大器是更好的选择。这完全是由于FET放大器具有更高的输入阻抗，这将减少网络的负载。

最后要注意的是：具有高Q值部分的滤波器会导致超出运算放大器的动态范围。这是由于该部分的峰值。Q引起的峰值将导致幅度A0:

一个0= H Q

还要记住：

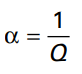
一个例子

例如，现在将设计一个抗混叠滤波器。

过滤器的规格如下：

截止频率为 8 kHz。

阻带衰减为 72 dB。这对应于 12 位系统。

阻带频率为 42 kSPS。这假设使用100 kSPS A/D转换器。奈奎斯特频率为 50 kHz。减去 8 kHz，对于采样率周围的通带图像，得到 42 kHz。

选择巴特沃兹滤波器响应是为了在衰减和相位响应之间做出最佳折衷。

采用巴特沃兹曲线（图1），在72 dB处绘制一条水平线。在 5.25 Hz 处绘制一条垂直线。这是F的比率S/F0（见图 24）。这表明需要 5 的筛选顺序。然后，此信息将用于筛选器工具的输入。

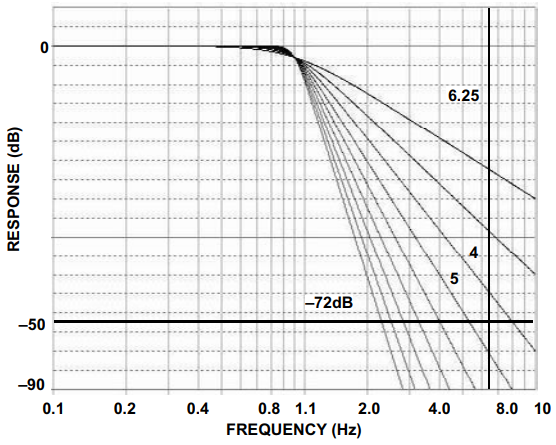
图 24.确定筛选顺序

使用该工具

首先，必须确定过滤顺序。为此，请使用图 24 中所述的滤波器响应曲线。

然后在设计工具中使用此信息。首先，输入过滤器响应。在本例中，选择低通。将显示其他选项。

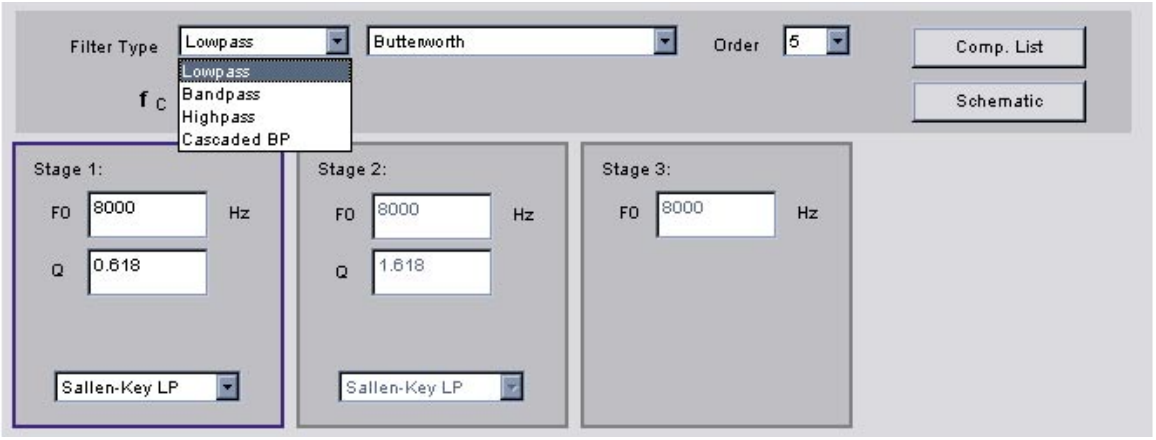
图 25.输入响应类型

接下来，输入响应形状。巴特沃斯被选中。

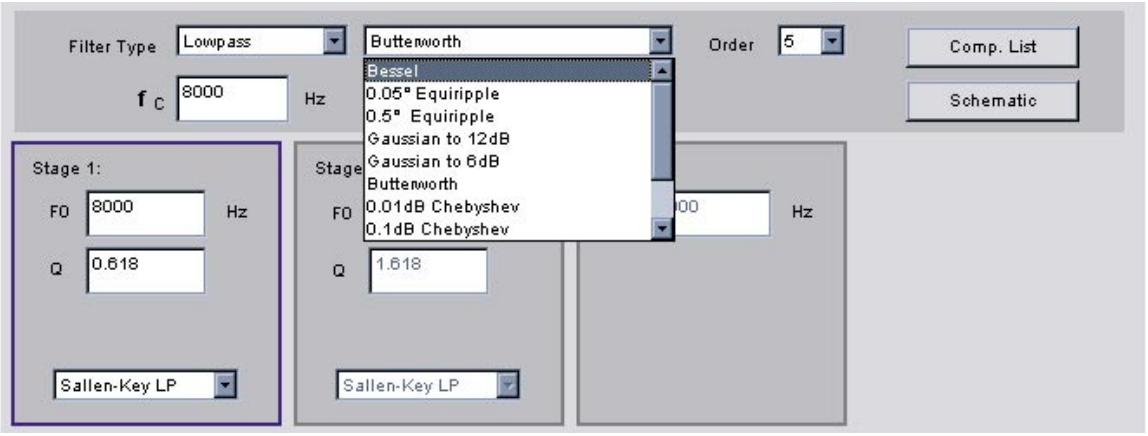
图 26.过滤器响应

然后输入筛选顺序。选项为 1 到 8。在此示例中，选择五阶。还输入截止（或中心）频率。

五阶滤波器由两个二阶部分和一个单极点部分组成。这将显示在工具的下一行框中。对于每个二阶部分，输入滤波器的拓扑。活动框的轮廓。

这些部分可以按任意顺序进行配置。通常，低Q值部分放在第一位。这可能有助于解决超出滤波器动态范围的问题，在较高Q值部分达到峰值之前提供一些衰减。

滤波器工具为每个二阶截面输入了适当的中心频率和Q，并为单极输入了中心频率。请注意，对于自定义筛选器，可以手动输入这些值。然后从给定的选项中输入滤波器拓扑。每个部分都是独立的（图 27）。

然后输入各个部分的详细信息。由于实际元件值是比率值，因此必须指定一个值，然后确定其余值。之所以选择设置电容，是因为选择值的自由度通常低于电阻（图 28）。

接下来输入增益。这通常需要用户输入另一个组件值。对于单位增益Sallen-Key部分的具体示例，反馈电阻的值可以指定为0 Ω。组件条目上有一些错误检测。对于状态变量和双二阶部分，输入其他电阻值。

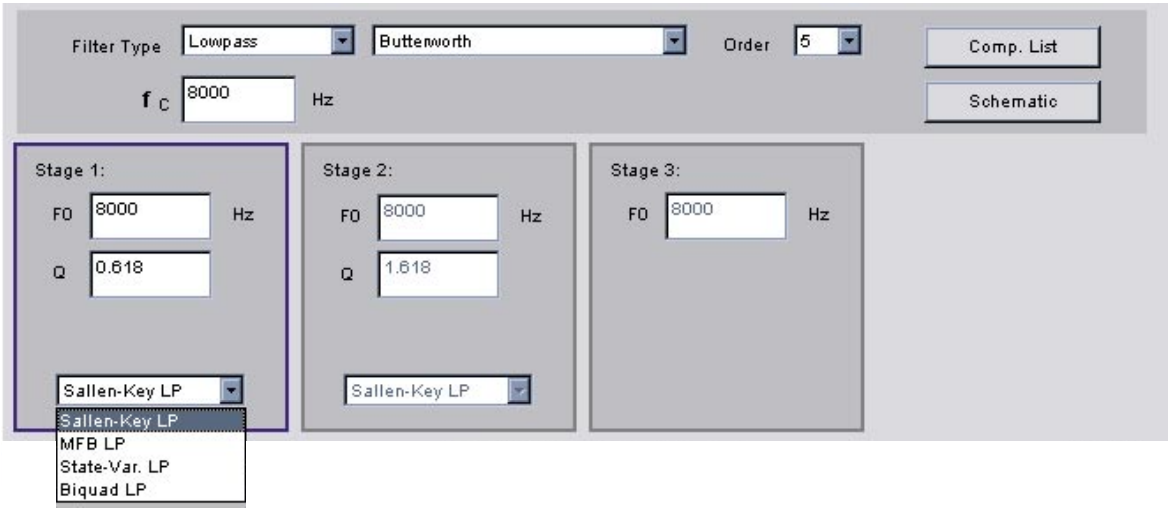
图 27.筛选器拓扑

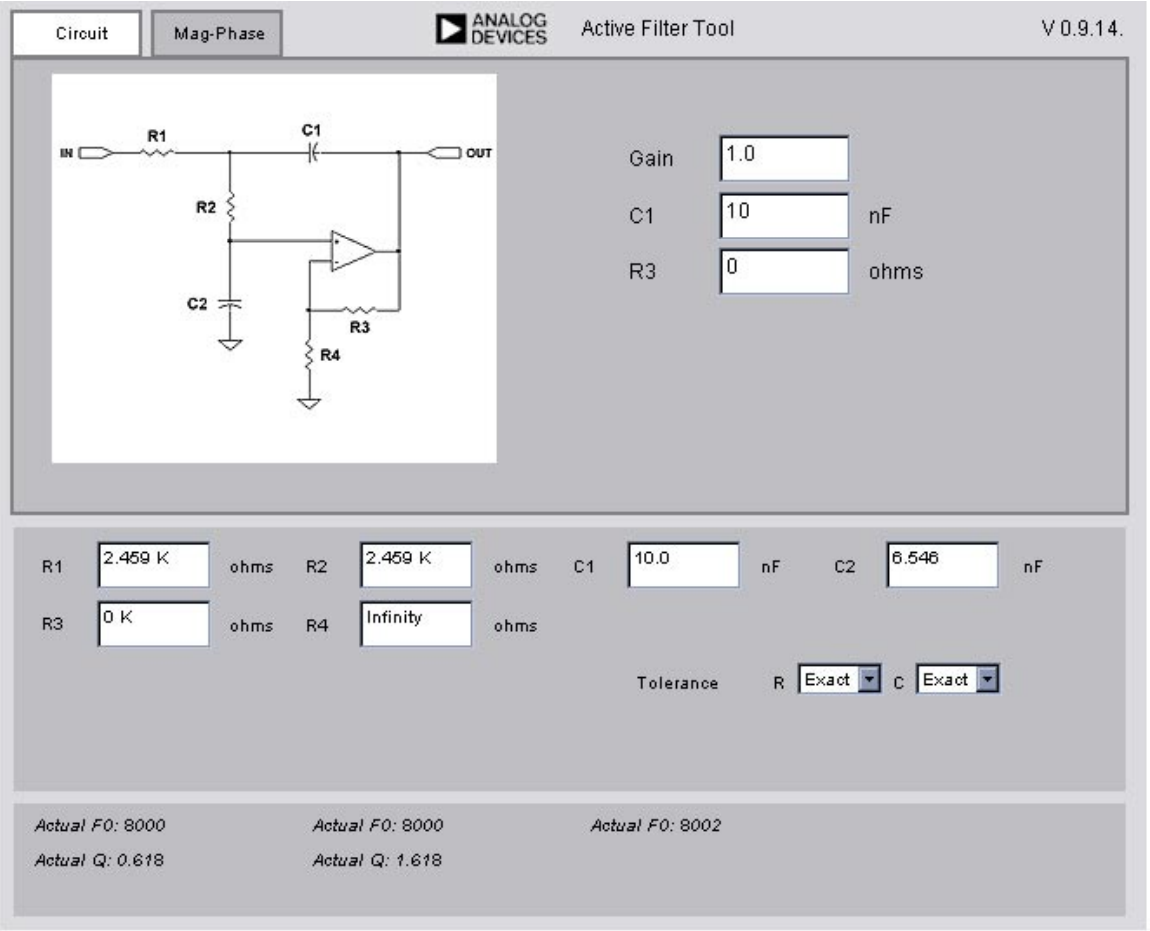
图 28.组件值（精确）

这些值是确切的计算值。筛选器通常使用标准值组件构建。该工具允许用户指定组件公差。完成此操作后，将在框中替换标准值。此外，F 中的百分比误差0并计算由值变化引起的Q。对于自定义筛选器，可以手动输入值。

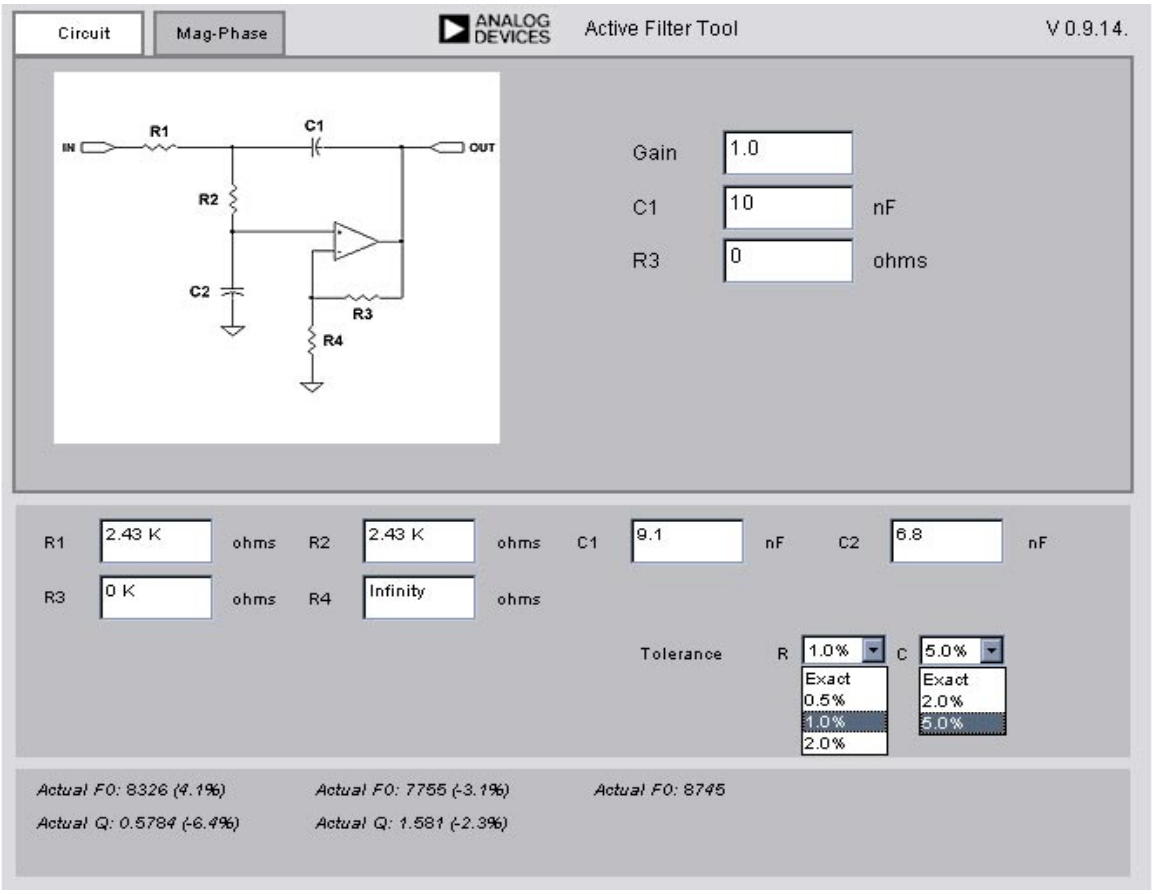
图 29.组件值（标准）

图30显示了由于使用标准值与精确值而导致的滤波器响应变化。这是否可以接受是设计师必须做出的决定。

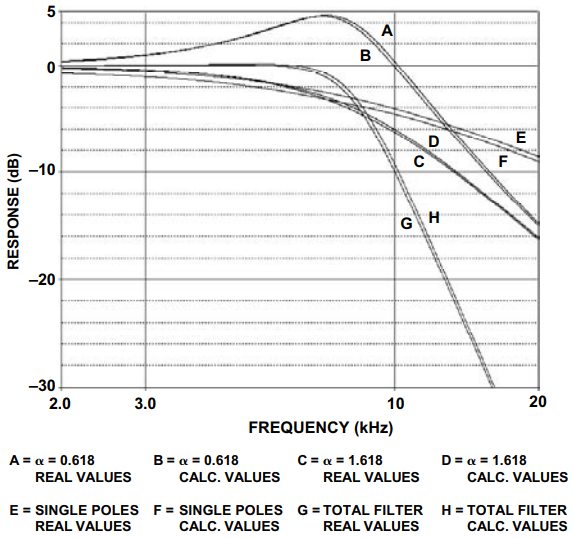
图 30.标准值引起的滤波器响应变化

审核编辑：郭婷