基于模糊控制的水下潜器沉浮控制方法

 

　　文中针对实际要求，提出一种基于自适应模糊控制的水下潜器自动沉浮控制方法。由于模糊控制器的隶属函数与模糊控制规则的选取对控制效果影响最大，该方法从优化隶属函数入手，采用多层前向神经网络的误差反向传播(EBP)算法对它的参数进行在线修正，采用Delta-Bar-Delta学习规则对学习速率进行在线调整，使EBP算法具有较快的收敛速度，同时避免了局部极小值问题。仿真实验表明，对于水下潜器自动沉浮与定深潜伏运动的不能精确建摸、干扰严重的非线性、时变情况，这种自适应模糊控制是一种较好的控制方式。

　　1 潜器水下自主沉浮控制系统工作原理

　　潜器沉浮控制系统装置如图1所示，主要由油箱、油泵、电磁阀、油囊及相关的电子控制器、传感器，模糊转换电路、电源组成。装置浮力调节的控制原理是用油泵将油箱的油充到油囊中去，油囊膨胀，从而使反潜器排水体积增加，其浮力增加。反之，将油囊中的油抽回油箱中，则其浮力将减小。正负浮力的改变从而使反潜器上浮或下沉。

　　

 

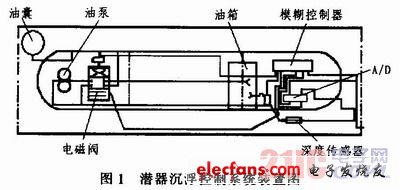
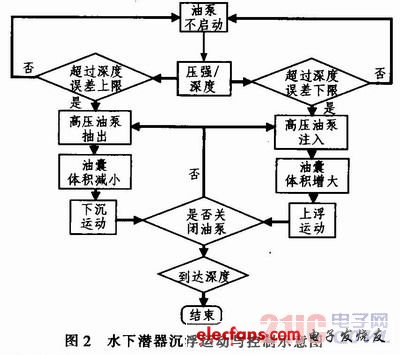
　　设想的潜器定深与沉浮运动的过程描述如图2所示。所构想的初始技术指标为：定深误差在定深指标的5%以内，即在2 000 m定深处上下沉浮不能超出100 m。这样就要求高压油泵的工作深度要达到2 100 m以上，并留出50～100 m的设计裕度。油囊高压泵的抽放油速率设计以及油囊的大小，一方面根据要求的反潜器定深动作反应速率和油囊体积变化时滞来参考，另一方面这些性能参数也依赖于实验精确测定，为油囊充放油控制提供参数。

　　

 

　　2 自适应模糊控制方法

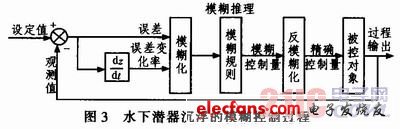
　　基于自适应模糊控制的水下潜器沉浮控制过程，如图3所示。

　　

 

　　2.1 模糊控制器

　　模糊控制器采用二维模糊控制器，用深度的偏差E和偏差变化率

　　

 

　　为它的2个输入，以电磁阀的变化μ作为控制量，将

　　

 

　　和控制量μ的数量范围划分为5个用语言变量表述的模糊集，即负大(NB)、负小(NS)、零(0)、正小(PS)、正大(PB)。而E和

　　

 

　　的数量范围亦划分为5个语言变量表述的模糊集，即负大(NB)、负小(NS)、零(0)、正小(PS)、正大(PB)。

　　2.2 隶属函数

　　输入变量的隶属函数为梯形隶属函数和三角形隶属函数。下面给出的是控制变量的隶属函数，输入变量的隶属函数类同。

　　

 

　　其中i为输入变量：i=1对应E，i=2对应

　　

 

　　;j为规则;μij(xi)为规则j中第i个输入分量在所在模糊区间上的隶属度;a，b，c，d为规则j中第i个输入分量所在模糊区间的控制参数。

　　2.3 自适应模糊控制器

　　对模糊控制器的修正，实际上是对隶属函数的参数a，b，c，d和

　　修正。取误差函数：

　　

 

　　其中，η(t)为深度H，dp为控制目标。

　　采用EBP算法(加惯性项)对隶属函数的参数进行修正，得如下公式：

　　

 

　　其中，αij、βij、γij均为学习速率，τi为惯性系数。

　　上述3式中右边第3项为惯性项，因为在EBP算法中，如果学习速率取的小学习过程将很慢，而大的学习速率又可能导致学习过程的振荡，另外学习过程可能收敛于局部极小点或在误差函数的平稳段停止不前。惯性项的引入可以提高收敛速度和改善动态性能(即可以抑制寄生振荡)。

　　

 

　　

 

　　针对EBP算法收敛速度慢的问题，采用Delta-Bar-Delta学习规则对学习速率进行在线调整，以提高收敛速度。

　　以αij为例，βij、γij同理：

　　

 

　　其中，ξ是一个正实数，参数a、b、ξ根据实际情况自定。典型值为：10-4≤a≤0.1，0.1≤b≤0.5，0.1≤ξ≤0.7。

　　3 仿真分析

　　假定潜器在水下1 990 m处于悬浮平衡状态，油泵充抽油率为10 N/S，突然受到一瞬时外力的扰动作用，使得潜器获得了向上或向下的速度(12 m/s或-12 m/s)。利用计算机仿真潜器在基于自适应模糊控制方法下的沉浮控制效果，仿真效果如图4、图5所示。仿真结果表明：采用自适应模糊控制方法实现对水下潜器的自主沉浮控制是完全可行的，能够在受到一定扰动的情况下仍保持定深悬浮的稳定状态。

　　

 

　　

 

　　4 结束语

　　良好的自动沉浮控制能力对于水下潜器来说是至关重要的，是保证水下潜器能够进行正常工作的前提条件。由于水下潜器在水下的低速运动表现为耦合非线性，因此，水下潜器自动沉浮控制系统必然是一种惯性大、时滞、非线性的复杂控制系统。本文提出的基于模糊控制的沉浮控制方法从优化隶属函数入手，采用多层前向神经网络的误差反向传播(EBP)算法对它的参数进行在线修正，并采用Delta-Bar-Delta学习规则对学习速率进行在线调整，使EBP算法具有较快的收敛速度，同时避免了局部极小值问题，在实际工程中具有广阔的应用前景。此外，隶属函数的优化还可以考虑将神经网络与其他智能方法相结合，以期能够获得更快的控制效果。