

AQI分析与预测-1
描述
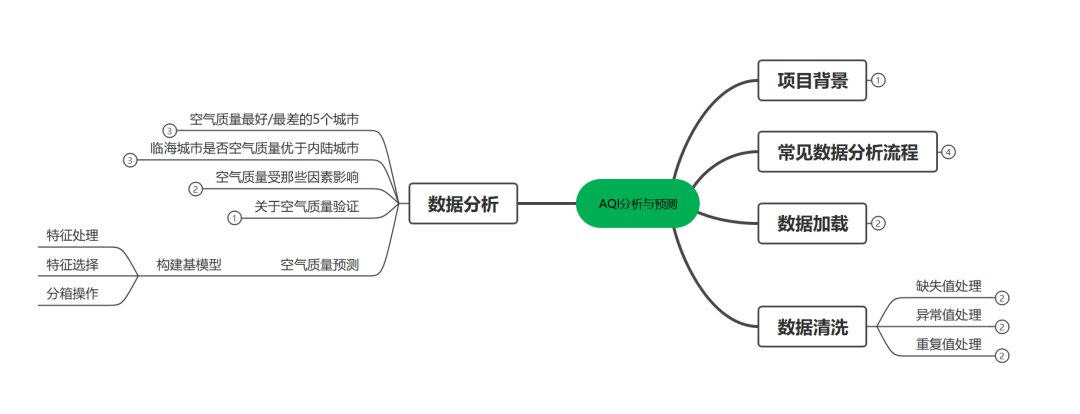
一.项目背景
AQI(air Quality Index)指空气质量指数,用来衡量空气清洁或者污染程度。值
越小,表示空气质量越好。近年来因为环境问题,空气质量越来越受到人们重视。
二.实现过程
1.数据加载
1)读取数据
2)查看数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
sns.set(style="darkgrid", font_scale=1.2)
plt.rcParams["font.family"] = "SimHei"
plt.rcParams["axes.unicode_minus"] = False
warnings.filterwarnings("ignore")
#读取文件
data = pd.read_csv("data.csv")
#输出数据形状
print(data.shape)
#查看数据
data.head()

2.数据清洗
1)缺失值处理
2)异常值处理
3)重复值处理
1)缺失值处理
》》查看缺失值
》》缺失值填充
#计算缺失值比例
t = data.isnull().sum()
#链接数据
t = pd.concat([t, t / len(data)], axis=1)
#设置列名称
t.columns = ["缺失值数量", "缺失值比例"]
#显示表格
display(t)
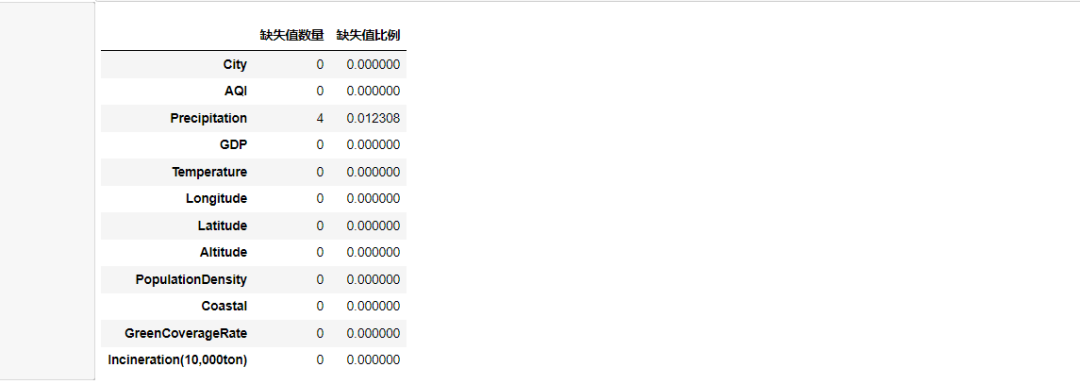
#计算降雨量偏度,偏度较小
print(data["Precipitation"].skew())
#绘制图形
sns.distplot(data["Precipitation"].dropna())
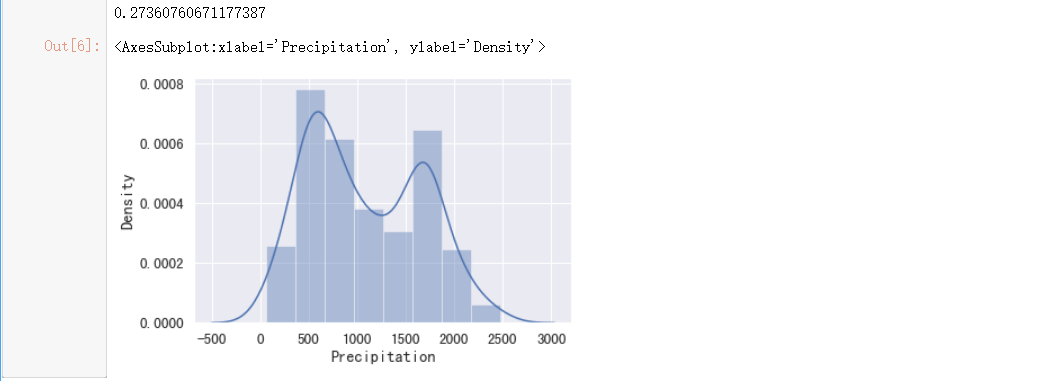
#用中位数填充缺失值
data.fillna({"Precipitation": data["Precipitation"].median()}, inplace=True)
#计算缺失值
data.isnull().sum()

2)异常值处理
》》查看异常值
》》异常值处理
#查看数据分布情况
data.describe()
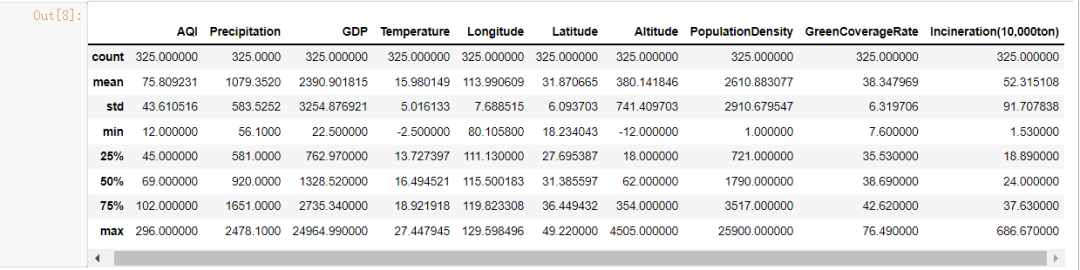
#绘制图形
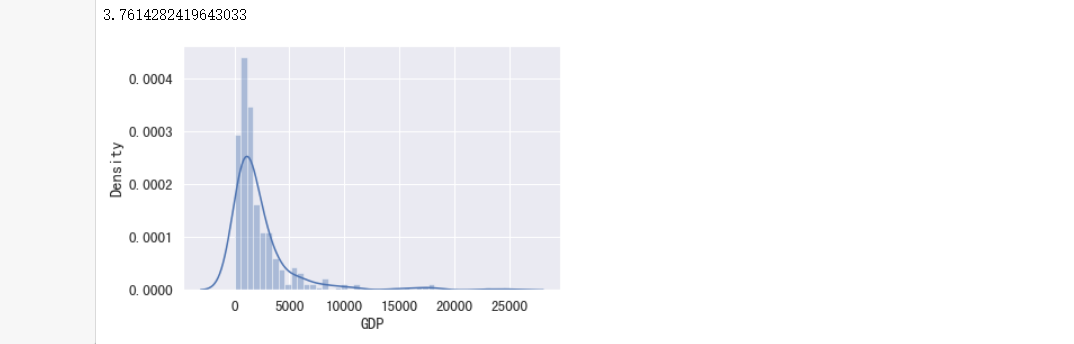
sns.distplot(data["GDP"])
#输出GDP峰值,偏度较大
print(data["GDP"].skew())
#计算均值和标准差
mean, std = data["GDP"].mean(), data["GDP"].std()
#计算下限与上限
lower, upper = mean - 3 * std, mean + 3 * std
#均值
print("均值:", mean)
#标准差
print("标准差:", std)
#下限
print("下限:", lower)
#上限
print("上限:", upper)
#获取在3倍标准差之外的数据。
data["GDP"][(data["GDP"] < lower) | (data["GDP"] > upper)]

#绘制箱线图
sns.boxplot(data=data["GDP"])
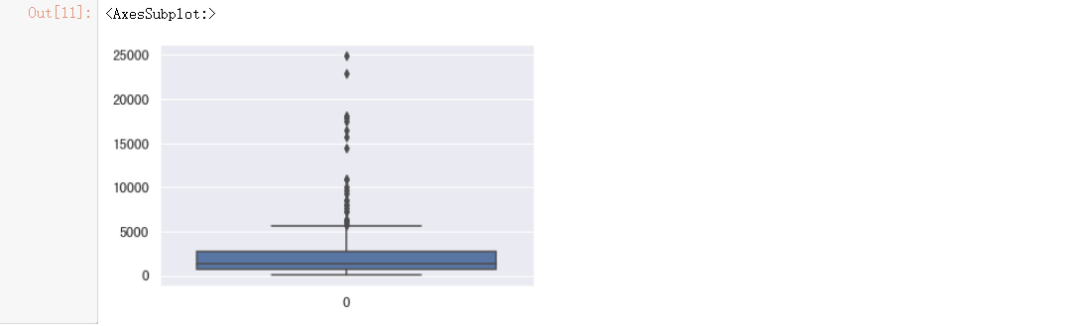
#初始画布
fig, ax = plt.subplots(1, 2)
#设置画布大小
fig.set_size_inches(15, 5)
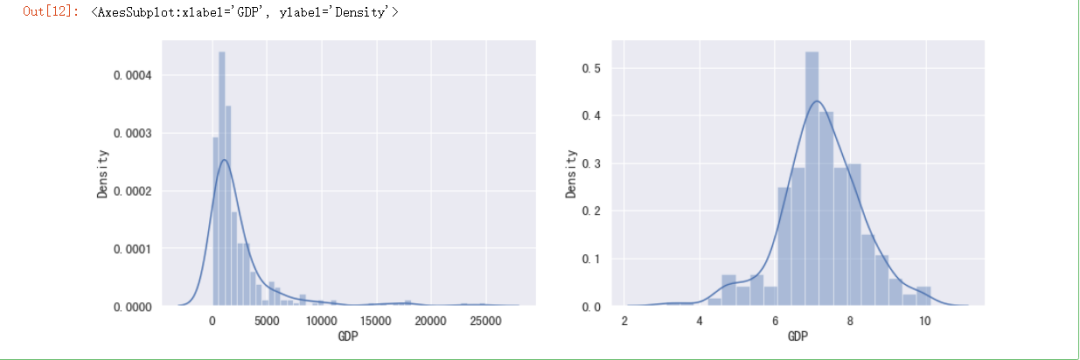
#绘制直方图
sns.distplot(data["GDP"], ax=ax[0])
#绘制对数直方图
sns.distplot(np.log(data["GDP"]), ax=ax[1])
3)重复值处理
》》查看重复值
》》删除重复值
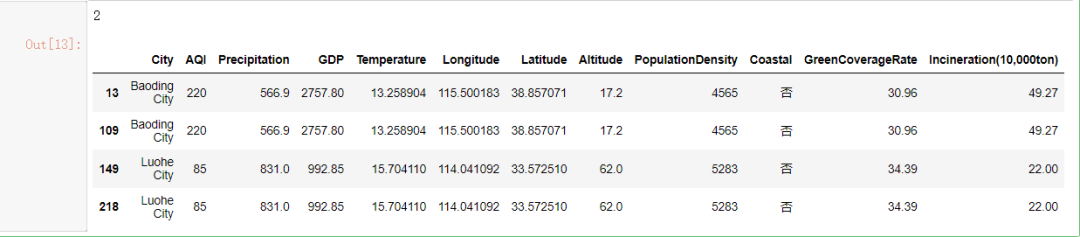
#发现重复值。
print(data.duplicated().sum())
#查看哪些记录出现了重复值。
data[data.duplicated(keep=False)]
#删除重复值
data.drop_duplicates(inplace=True)
#统计重复值
data.duplicated().sum()

3.数据分析
1)空气质量最好/最差的5个城市
2)临海城市是否空气质量优于内陆城市
3)空气质量受那些因素影响
4)关于空气质量验证
1)空气质量最好/最差的5个城市
》》筛选数据
》》按照AQI排序
》》绘图观察
#空气质量最好的5个城市
#筛选数据,按照AQI升序排列,
t = data[["City", "AQI"]].sort_values("AQI")
#筛选数据
t = t.iloc[:5]
#显示数据
display(t)
#旋转x轴标签
plt.xticks(rotation=30)
#绘制柱状图
sns.barplot(x="City",
y="AQI",
data=t)
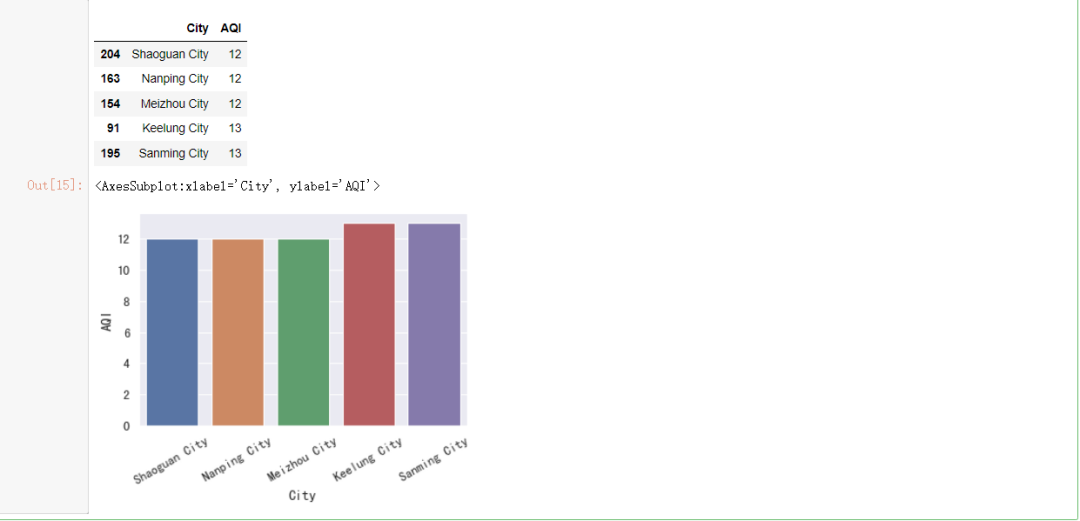
我们发现空气质量最好的5个城市:
1.韶关市
2.南平市
3.梅州市
4.基隆市
5.三明市
#空气质量最差的5个城市
#筛选数据,按照AQI降序排列
t = data[["City", "AQI"]].sort_values("AQI", ascending=False)
#筛选前5条数据
t = t.iloc[:5]
#显示数据
display(t)
#旋转x轴标签
plt.xticks(rotation=45)
sns.barplot(x="City",
y="AQI",
data=t)
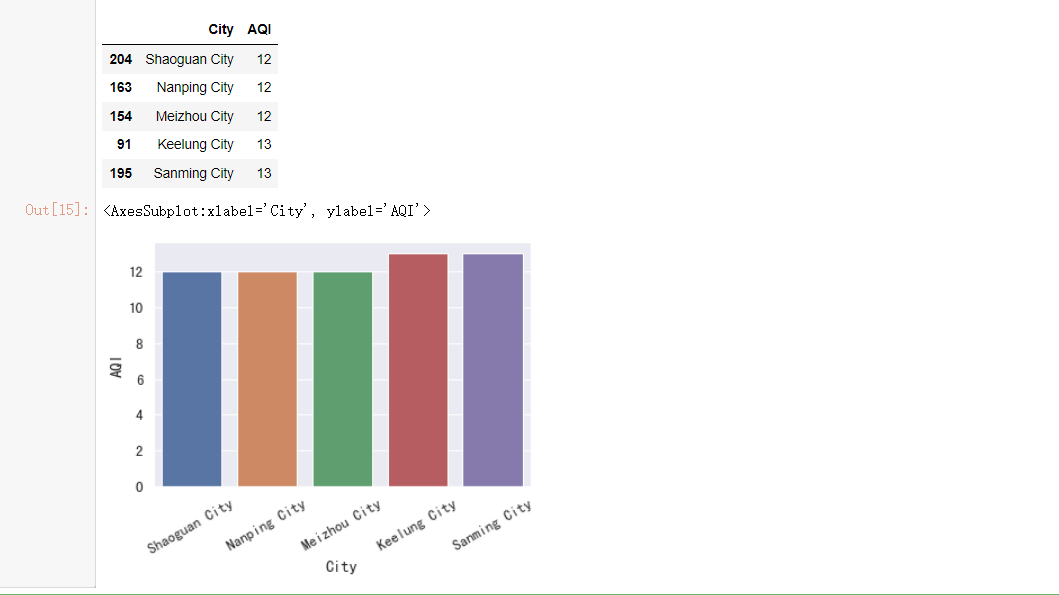
我们发现空气质量最差的5个城市:
1.北京市
2.朝阳市
3.保定市
4.锦州市
5.焦作市
对于AQI,对空气质量进行等级划分,划分表转如下
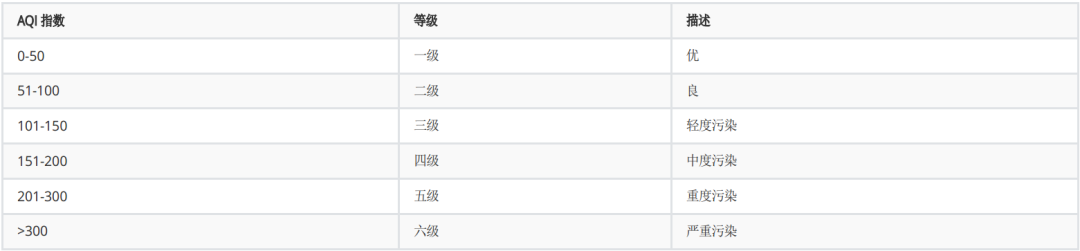
# 编写函数,将AQI转换为对应的等级。
def value_to_level(AQI):
if AQI >= 0 and AQI <= 50:
return "一级"
elif AQI >= 51 and AQI <= 100:
return "二级"
elif AQI >= 101 and AQI <= 150:
return "三级"
elif AQI >= 151 and AQI <= 200:
return "四级"
elif AQI >= 201 and AQI <= 300:
return "五级"
else:
return "六级"
#转换等级
level = data["AQI"].apply(value_to_level)
#输出统计
print(level.value_counts())
#绘制条形图观察数值
sns.countplot(x=level,
order=["一级", "二级", "三级", "四级", "五级", "六级"])
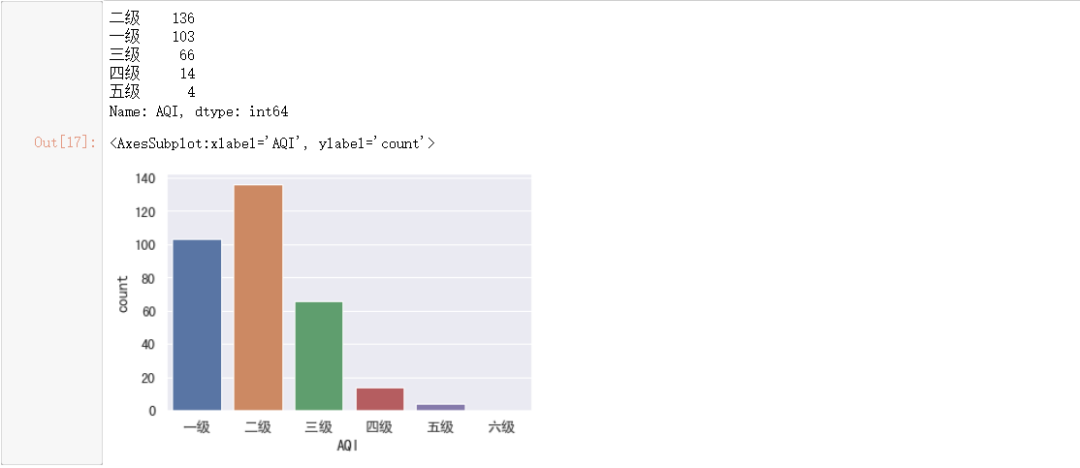
2)临海城市是否空气质量优于内陆城市
》》数量统计
》》分布统计
》》统计分析
绘制全国城市空气质量指数分布图
#绘制散点图
sns.scatterplot(x="Longitude",
y="Latitude",
hue="AQI",
palette=plt.cm.RdYlGn_r,
data=data)
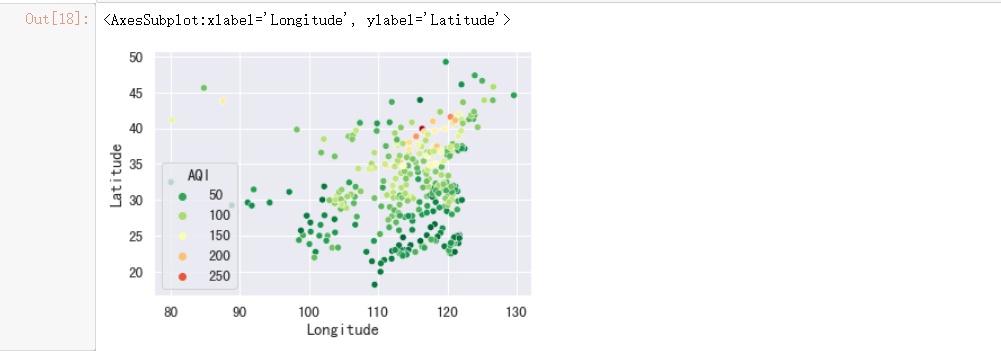
1)数量统计
我们统计下临海城市与内陆城市数量
#输出统计值
print(data["Coastal"].value_counts())
#绘制直方图
sns.countplot(x="Coastal",
data=data)
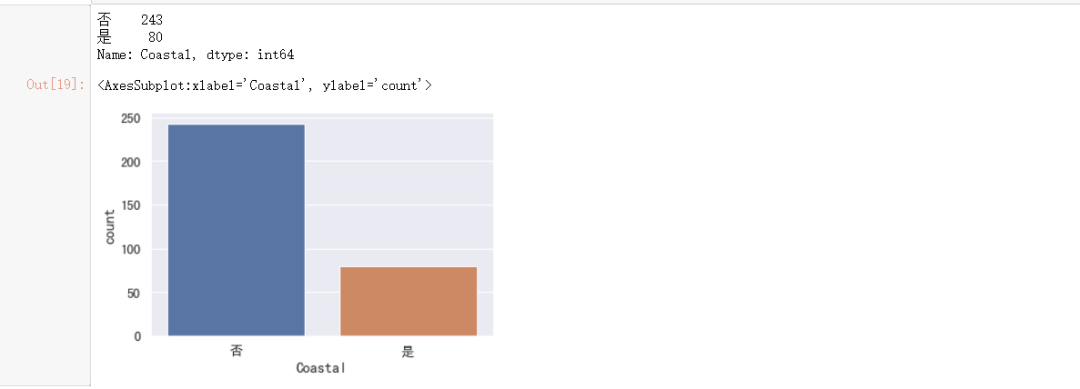
2)分布统计
我们观察下临海城市与内陆城市散点分布
sns.stripplot(x="Coastal",
y="AQI",
data=data)
结论:沿海城市空气质量普遍好于内陆城市
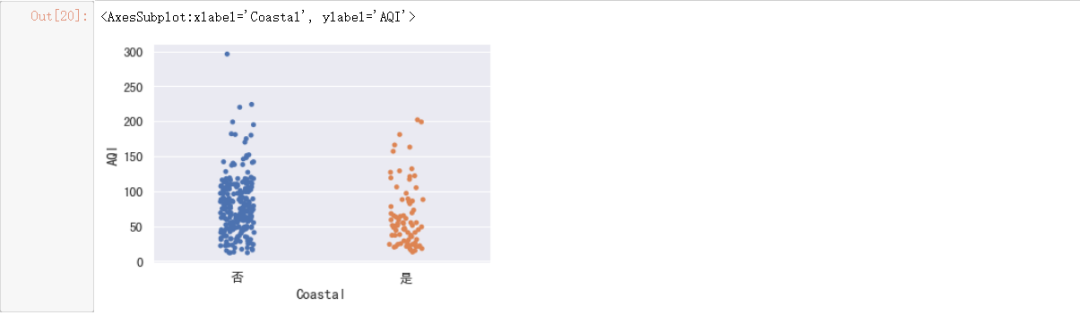
3)对以上结论进行统计分析
》》参数检验
》》非参数检验
参数检验
》》正态分布检验
》》方差齐性检验
》》两独立样本t检验
from scipy import stats
#分别获取临海与内陆城市两个样本的AQI值。
coastal = data[data["Coastal"] == "是"]["AQI"]
inland = data[data["Coastal"] == "否"]["AQI"]
#初始画布与坐标系
fig, ax = plt.subplots(1, 2)
#设置画布大小
fig.set_size_inches(15, 5)
#绘制两个样本的分布。
sns.distplot(coastal, ax=ax[0])
sns.distplot(inland, ax=ax[1])
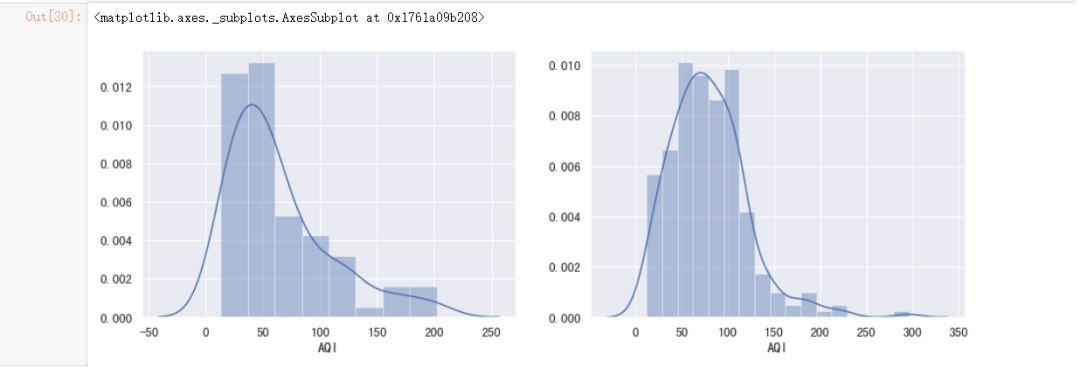
1.正态分布检验
》》绘制数据分布图
》》绘制PP图和QQ图
》》使用假设检验
PP图与QQ图
PP图(Probability-Probability plot)与QQ图(Quantile-Quantile plot)本质上基本是相同的。用于检验样本数据的分布是否符合某个分布(默认为正态分布)。
PP图:通过累积概率密度来检测。
x轴:根据传递的数据数量(n),计算x轴的绘制位置(x坐标),值为(1/n+1, 2/n+1, …… n/n+1)。
y轴:将样本数据排序,然后进行标准化(减均值除以标准差),计算样本数据在理论分布下的cdf值(累积概率密度)。
QQ图:通过分布百分比对应的数值来检测。
x轴:根据传递的数据数量(n),计算值(1/n+1, 2/n+1, …… n/n+1)的值。然后对每个值,计算在理论分布下的ppf值(cdf的逆运算,即根据累积概率密度求解对应
的位置)。
y轴:将数值排序,将每个数值标准化。
import statsmodels.api as sm
def plot_pp_qq(d):
"""
绘制PP图与QQ图的函数。
Parameters
----------
d : array-like
要绘制的数值。
"""
#初始化坐标系与画布
fig, ax = plt.subplots(1, 2)
#设置尺寸大小
fig.set_size_inches(15, 5)
#标准化
scale_data = (d - d.mean()) / d.std()
#创建ProbPlot对象,用于绘制pp图与qq图
#data:样本数据。
#dist:分布,默认为正态分布。数据data会与该分布进行对比
p= sm.ProbPlot(data=scale_data,
dist=stats.norm)
#绘制pp图
p.ppplot(line="45",
ax=ax[0])
#设置名称
ax[0].set_title("PP图")
#绘制qq图
p.qqplot(line="45",
ax=ax[1])
#设置名称
ax[1].set_title("QQ图")
#显示图形
plt.show()
#绘制沿海城市图形
plot_pp_qq(coastal)
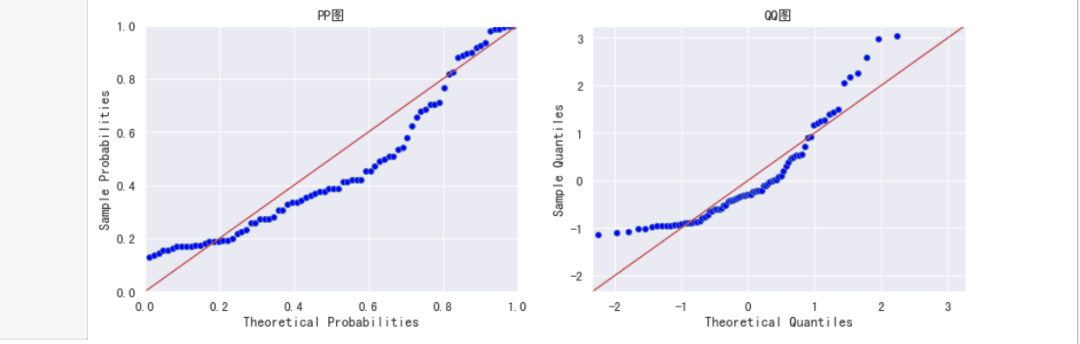
#绘制内陆城市图形
plot_pp_qq(inland)
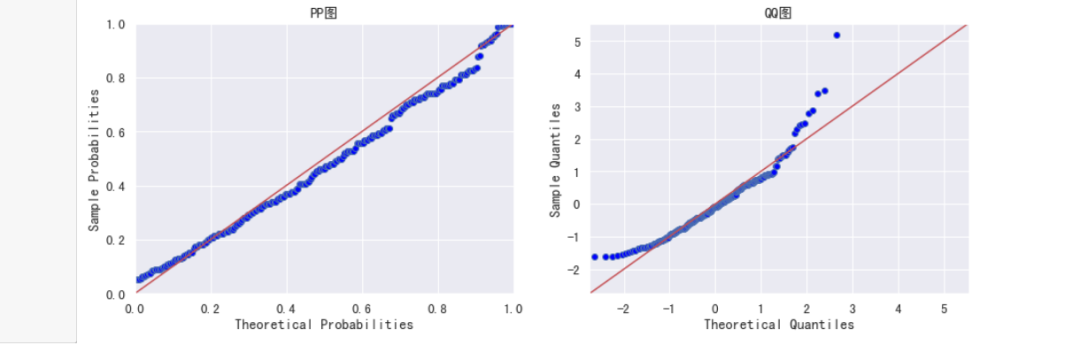
进行是否正态分布检验?
#原假设:观测值来自于正态分布的总体。
#备则假设:观测值并非来自正态分布的总体。
print(stats.normaltest(coastal))
print(stats.normaltest(inland))
结论:很遗憾,两样本正态分布可能性为0
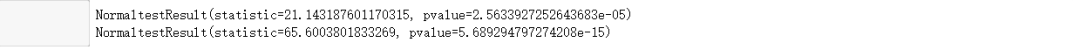
接下来我们处理方法:
》》将分布转换为正态分布
》》使用非参数检验
》》样本容量较大时,可以近似使用z检验

#将数据转换为正态分布
bc_coastal, _ = stats.boxcox(coastal)
bc_inland, _ = stats.boxcox(inland)
#初始画布与坐标系
fig, ax = plt.subplots(1, 2)
#设置画布大小
fig.set_size_inches(15, 5)
#绘制两个样本的分布。
sns.distplot(bc_coastal, ax=ax[0])
sns.distplot(bc_inland, ax=ax[1])
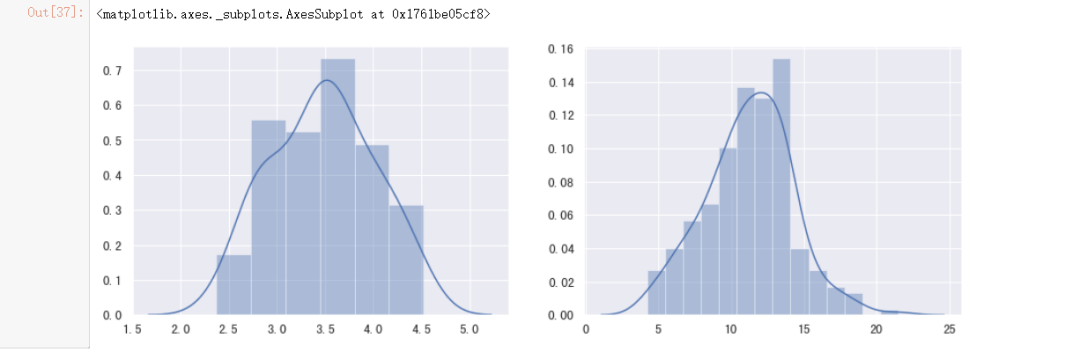
#绘制转换后的pp图与qq图
plot_pp_qq(bc_coastal)
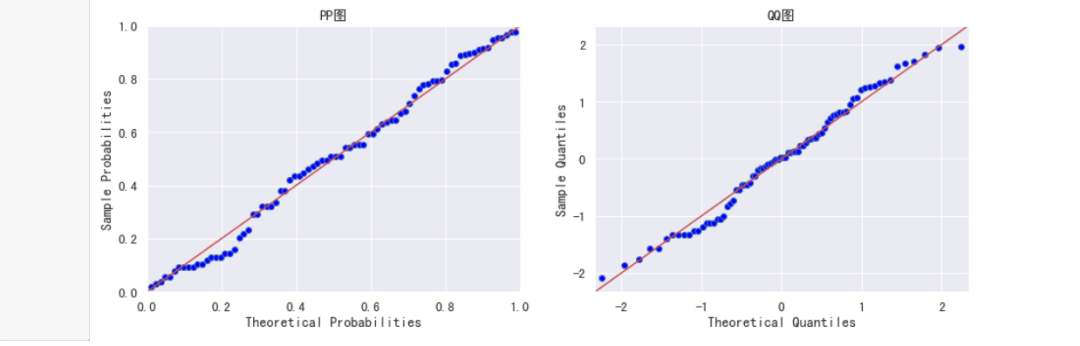
#绘制转换后的pp图与qq图
plot_pp_qq(bc_inland)
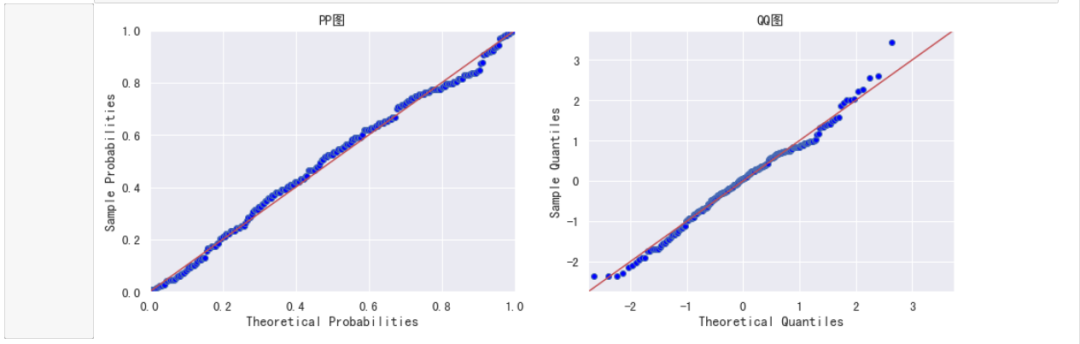
#再次进行正态性检验
print(stats.normaltest(bc_coastal))
print(stats.normaltest(bc_inland))
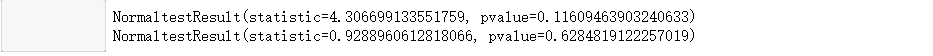
# 进行方差齐性(方差是否相等)检验。为后续的两样本t检验服务。
# 原假设:多个样本的方差相等。
# 备则假设:多个样本的方差不等。
stats.levene(bc_coastal, bc_inland)
结论:方差不等。

# 进行两样本t检验。
# equal_var:方差是否齐性(相等)。
# 原假设:两独立样本均值相等。
# 备则假设:两独立样本均值不等。
r = stats.ttest_ind(bc_coastal, bc_inland, equal_var=False)
print(r)
结论:两独立样本均值不等,说明沿海城市空气质量普遍好于内陆城市。

#非参数检验
# 曼-惠特尼检验。应该仅在每个样本容量 > 20时使用。
# 原假设:两个样本服从相同的分布。
# 备则假设:两个样本服从不同的分布。
print(stats.mannwhitneyu(coastal, inland))
# 威尔科克森秩和检验。
# 原假设:两个样本服从相同的分布。
# 备则假设:两个样本服从不同的分布。
print(stats.ranksums(coastal, inland))
结论:两个样本服从不同的分布。
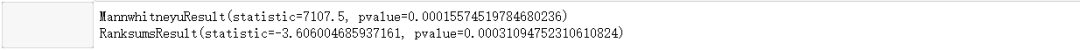
近似使用z检验:当样本量足够大时,即使总体不服从正态分布,也可以使用z检验进行检验.
#方差齐性检验
stats.levene(coastal, inland)
结论:方差相同

#进行t检验
r = stats.ttest_ind(coastal, inland, equal_var=True)
#输出结果
print(r)
结论:两独立样本均值不等,与之前结论一致,更进一步说明沿海城市空气质量普遍好于内陆城市。

声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
跪求各路大神labview如何计算AQI2025-05-19 6076
-
电磁轨迹预测分析系统2024-06-25 957
-
AQI空气质量监测站——保护空气质量的重要一环2023-07-18 3643
-
AQI空气质量监测站的重要性-欧森杰2023-06-19 1135
-
预测分析介绍及行业应用案例2023-05-30 1018
-
AQI分析与预测-22023-02-23 2114
-
MAX6921AQI+ PMIC - 显示驱动器2023-02-10 117
-
光伏功率预测有哪些作用2021-07-07 1713
-
微型空气质量监测仪【恒美仪器HM-AQI】解决方案2021-05-19 972
-
使用预测模型预测图片出现错误提示in_dims[1]:32 != filter_dims[1] * groups:3的解决方法2019-03-07 1616
-
数据预测分析方法2016-01-15 867
-
CCD图像分析方法和预测算法???2012-07-01 2603
-
经济预测模型2011-08-15 2193
-
PCB产业投资预测分析2009-12-31 856
全部0条评论

快来发表一下你的评论吧 !

