

AQI分析与预测-2
描述
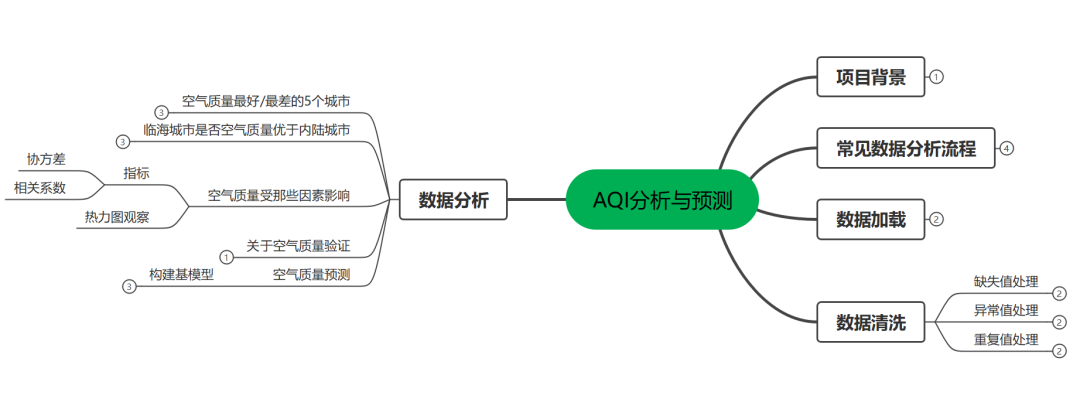
一.项目背景
AQI(air Quality Index)指空气质量指数,用来衡量空气清洁或者污染程度。值
越小,表示空气质量越好。近年来因为环境问题,空气质量越来越受到人们重视。
上篇文章[AQI分析与预测(一)](http://mp.weixin.qq.com/s?__biz=MzIzODI4ODM2MA==&mid=2247486525&idx=1&sn=a92d40e0d715f9ab63563b4e8b054a0d&chksm=e93ae0bade4d69ac57407216484cdbb6d7a8a812baef1c0e4ab0d5aeae0c7f0aff9fd274127b&scene=21#wechat_redirect)我们进行了初步分析,主要分析了空气质量最好/差城市和临海城市是否空气质量优于内陆城市这两个问题,本篇我们在之前基础上继续研究如下问题。
1.空气质量受那些因素影响
2.关于空气质量验证
3.构建空气质量预测模型
二.实现过程
1.空气质量受那些因素影响
》》指标:协方差和相关系数
》》图形:热力图
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
sns.set(style="darkgrid", font_scale=1.2)
plt.rcParams["font.family"] = "SimHei"
plt.rcParams["axes.unicode_minus"] = False
warnings.filterwarnings("ignore")
#读取文件
data = pd.read_csv("data.csv")
#查看数据
data.head()

#kind:绘制图像的类型。可选值:
#scatter:散点图(默认值)。
#reg:带有回归线的散点图。
#vars:显示哪些变量之间的两两关系,默认为显示所有变量。
sns.pairplot(data, vars=["AQI", "PopulationDensity", "GreenCoverageRate"])
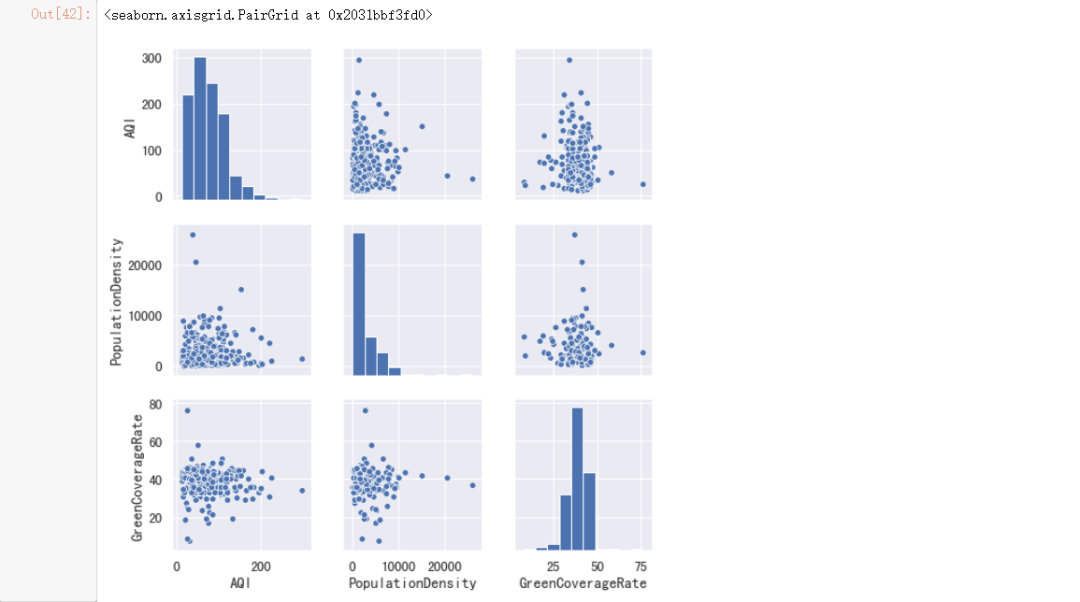

#计算相关数据
x = data["AQI"]
y = data["Precipitation"]
#计算AQI与Precipitation的协方差。
a = (x - x.mean()) * (y - y.mean())
#计算协方差
cov = np.sum(a) / (len(a) - 1)
print("协方差:", cov)


#计算AQI与Precipitation的相关系数。
corr = cov / np.sqrt(x.var() * y.var())
print("相关系数:", corr)

#pandas封装了相关方法
print("协方差:", x.cov(y))
print("相关系数:", x.corr(y))

#初始化画布
plt.figure(figsize=(15, 10))
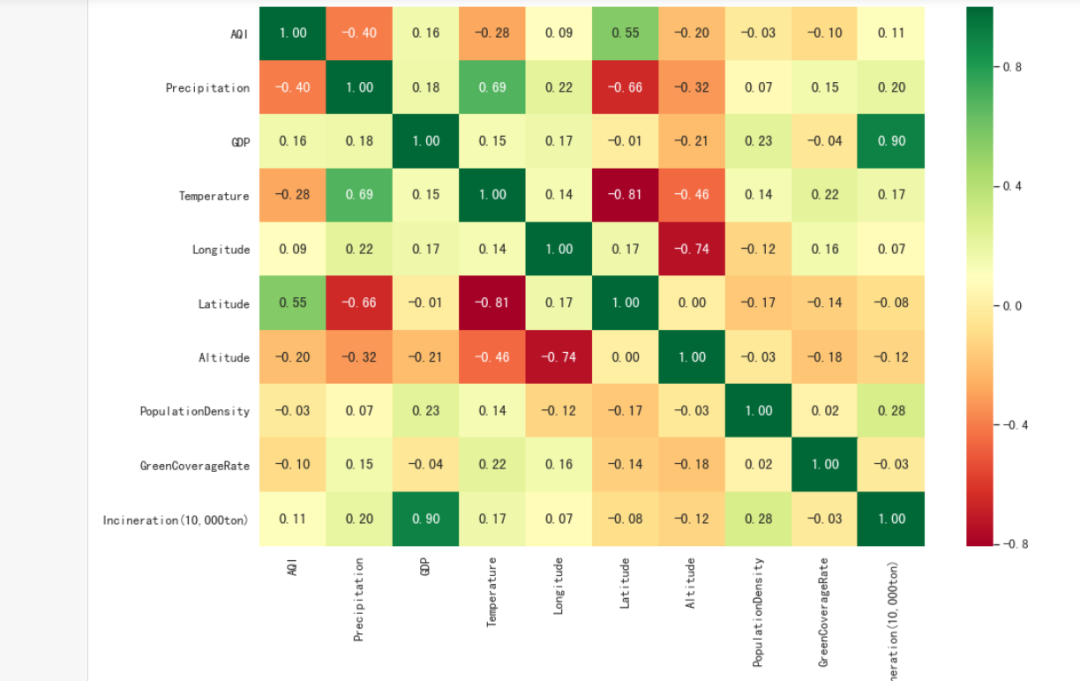
#绘制热力图
ax = sns.heatmap(data.corr(),
cmap=plt.cm.RdYlGn,
annot=True,
fmt=".2f")
结论:降雨量越多,空气质量越好;维度越低,空气质量越好
2.关于空气质量验证
》》问题:全国所有城市的空气质量指数均值在71左右,请问此结论准确吗?
》》方法:假设检验
该需求是验证样本均值是否等于总体均值,根据条件,我们可以使用单样本t检验,
置信度为95%。
#进行单样本t检验
r = stats.ttest_1samp(data["AQI"], 71)
#输出检验统计量
print("t值:", r.statistic)
#输出p值
print("p值:", r.pvalue)
结论:我们可以看到P值是大于0.05的,y因此我们无法拒绝原假设,因此接受原假设

#计算均值
mean = data["AQI"].mean()
#计算标准差
std = data["AQI"].std()
#计算置信区间
stats.t.interval(0.95, df=len(data) - 1, loc=mean, scale=std / np.sqrt(len(data)))
结论:我们就计算出全国城市平均空气质量指数,95%的可能大致在70.63~80.04之间

3.构建空气质量预测模型
》》对于一些城市,如果能够已知降雨量,温度,经纬度等指标,我们是否能够预测该
城市的空气质量指数呢?因此我们需要构建模型,预测新的数据。
》》过程:基模型构建,异常值处理后构建模型和特征选择后构建模型,将结果与基模
型进行对比,看看是否进行优化。
#进行类别转换
data["Coastal"] = data["Coastal"].map({"是": 1, "否": 0})
#统计类别数目
data["Coastal"].value_counts()
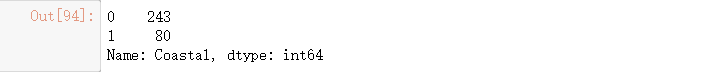
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
#City(城市名称)对预测毫无用处,删掉。
X = data.drop(["City","AQI"], axis=1)
#目标值
y = data["AQI"]
#分离测试集和训练集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
#构建基础线性回归模型
lr = LinearRegression()
#训练模型
lr.fit(X_train, y_train)
#输出训练集模型评分
print(lr.score(X_train, y_train))
#输出测试集模型评分
print(lr.score(X_test, y_test))

#绘制图形观察
#预测y值
y_hat = lr.predict(X_test)
#初始化画布
plt.figure(figsize=(15, 5))
#绘制真实值折线图
plt.plot(y_test.values,
"-r",
label="真实值",
marker="o")
#绘制预测值折线图
plt.plot(y_hat,
"-g",
label="预测值",
marker="D")
#设置图例
plt.legend(loc="upper left")
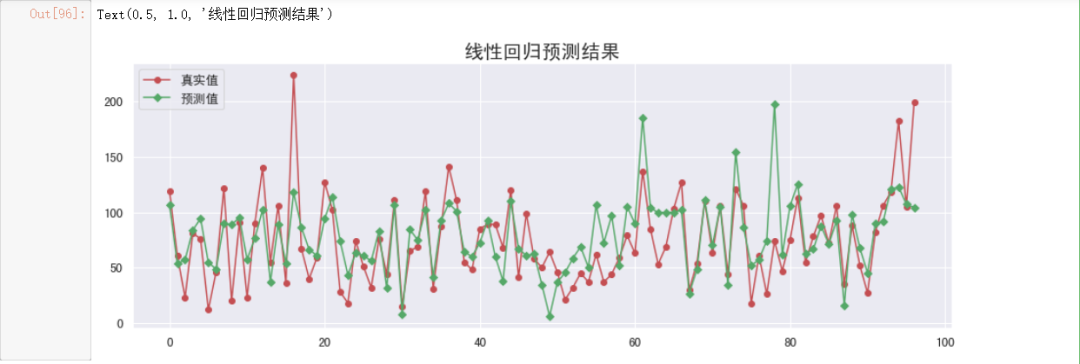
#设置标题
plt.title("线性回归预测结果", fontsize=20)
# Coastal是类别变量,映射为离散变量,不会有异常值。
#遍历列
for col in X.columns.drop("Coastal"):
#对数值型数据进行判断
if pd.api.types.is_numeric_dtype(X_train[col]):
#获取分位数
quartile = np.quantile(X_train[col], [0.25, 0.75])
#计算IQR
IQR = quartile[1] - quartile[0]
#计算正常数值下限
lower = quartile[0] - 1.5 * IQR
#计算正常数值上限
upper = quartile[1] + 1.5 * IQR
#用边界值进行填充异常值
X_train[col][X_train[col] < lower] = lower
X_train[col][X_train[col] > upper] = upper
X_test[col][X_test[col] < lower] = lower
X_test[col][X_test[col] > upper] = upper
#训练模型
lr.fit(X_train, y_train)
#去除异常值后评估模型效果
print(lr.score(X_train, y_train))
print(lr.score(X_test, y_test))
结论:去除异常值后所构建模型效果相比之前有所改进

#对数据进行标准化处理,
from sklearn.preprocessing import StandardScaler
#数据标准化
s = StandardScaler()
#对训练集进行标准化
X_train_scale = s.fit_transform(X_train)
#对测试集进行标准化
X_test_scale = s.transform(X_test)
#对数据进行特征选择,目的是提高模型准确率和训练速度
REFCV方法
》》RFE(REcursive feature elimination):递归特征消除,用来对特征进行重要性评级
》》CV(Cross Validation):交叉验证,通过交叉验证,选择最佳数量特征
具体过程如下:
RFE阶段:
1.初始特征集为所有可用特征
2.使用当前特征集进行建模,然后计算每个特征的重要性
3.删除最不重要的一个或者多个特征,更新特征集
4.跳到步骤2,直到完成所有特征集重要性评级
CV阶段
1.根据REF阶段确定的特征重要性,依次选择不同数量特征
2.对选定的特征集进行交叉验证
3.确定平均分最高的特征数量,完成特征选择。
from sklearn.feature_selection import RFECV
#estimator:要操作的模型。
#step:每次删除的变量数。
#cv:使用的交叉验证折数。
#n_jobs:并发的数量。
#scoring: 评估的方式。
rfecv = RFECV(estimator=lr,
step=1,
cv=5,
n_jobs=-1,
scoring="r2")
rfecv.fit(X_train_scale, y_train)
#返回经过选择之后,剩余的特征数量。
print(rfecv.n_features_)
#返回经过特征选择后,使用缩减特征训练后的模型。
print(rfecv.estimator_)
#返回每个特征的等级,数值越小,特征越重要。
print(rfecv.ranking_)
#返回布尔数组,用来表示特征是否被选择。
print(rfecv.support_)
#返回对应数量特征时,模型交叉验证的评分。
print(rfecv.grid_scores_)

#绘制图形
plt.plot(range(1, len(rfecv.grid_scores_) + 1),
rfecv.grid_scores_,
marker="o")
#设置x轴标签
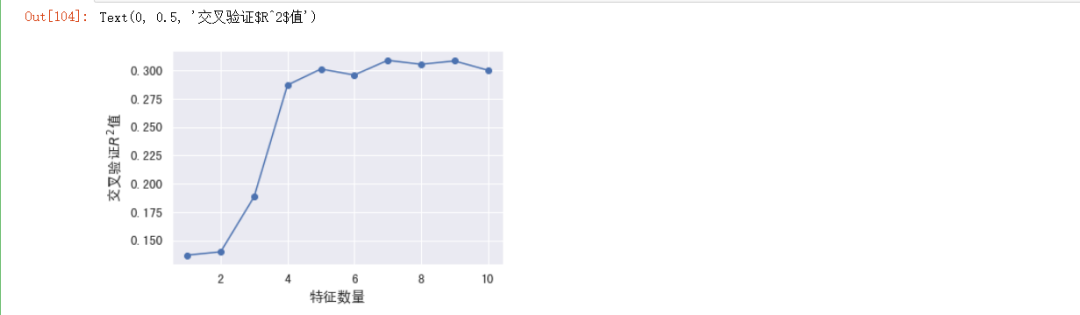
plt.xlabel("特征数量")
#设置y轴标签
plt.ylabel("交叉验证$R^2$值")
print("剔除的变量:", X.columns.values[~rfecv.support_])
#应用到训练集
X_train_eli = rfecv.transform(X_train_scale)
#应用到测试集
X_test_eli = rfecv.transform(X_test_scale)
#输出模型评分
print(rfecv.estimator_.score(X_train_eli, y_train))
print(rfecv.estimator_.score(X_test_eli, y_test))

#获取列名与对应的权重,构成一个元组,作为列表的元素。
li = list(zip(X.columns.values[rfecv.support_], rfecv.estimator_.coef_))
#根据权重的绝对值,对列表进行降序排列。
li.sort(key=lambda x: abs(x[1]), reverse=True)
#转换为Series
s = pd.Series(dict(li))
#初始化画布
plt.figure(figsize=(15, 5))
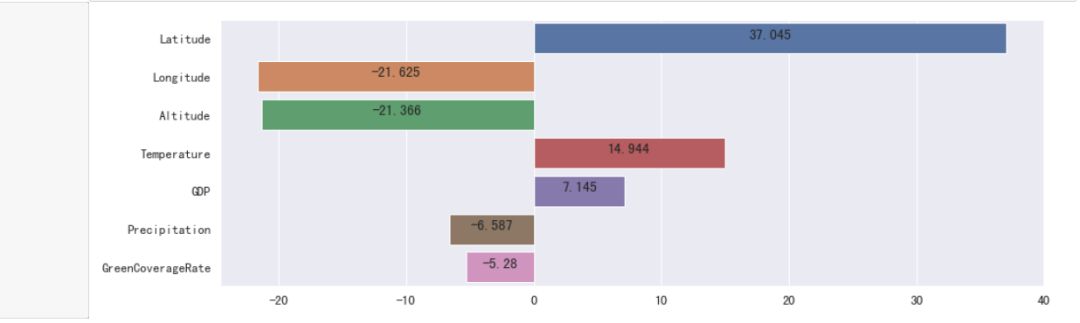
#绘制柱状图
ax = sns.barplot(y=s.index, x=s.values)
for y, x in enumerate(s):
#绘制标注
t = ax.text(x / 2, y, round(x, 3))
#设置居中对齐
t.set_ha("center")
#显示图形
plt.show()
from sklearn.preprocessing import KBinsDiscretizer
#KBinsDiscretizer K个分箱的离散器。用于将数值(通常是连续变量)变量进行区间离散化操作。
#n_bins:分箱(区间)的个数。
#encode:离散化编码方式。分为:onehot,onehot-dense与ordinal。
# onehot:使用独热编码,返回稀疏矩阵。
# onehot-dense:使用独热编码,返回稠密矩阵。
# ordinal:使用序数编码(0,1,2……)。
#strategy:分箱的方式。分为:uniform,quantile,kmeans。
#uniform:每个区间的长度范围大致相同。
#quantile:每个区间包含的元素个数大致相同。
#kmeans:使用一维kmeans方式进行分箱。
#对数据进行分箱操作
k=KBinsDiscretizer(n_bins=[4, 5, 10, 6],
encode="onehot-dense",
strategy="uniform")
#定义离散化的特征。
discretize=["Longitude", "Temperature", "Precipitation", "Latitude"]
#训练集数据转换为DataFrame
X_train_eli=pd.DataFrame(data=X_train_eli, columns=X.columns[rfecv.support_])
#测试集数据转换为DataFrame
X_test_eli=pd.DataFrame(data=X_test_eli, columns=X.columns[rfecv.support_])
#应用到训练集
r=k.fit_transform(X_train_eli[discretize])
r=pd.DataFrame(r, index=X_train_eli.index)
#获取除离散化特征之外的其他特征。
X_train_dis=X_train_eli.drop(discretize, axis=1)
#将离散化后的特征与其他特征进行重新组合。
X_train_dis=pd.concat([X_train_dis, r], axis=1)
#对测试集进行同样的离散化操作。
r=pd.DataFrame(k.transform(X_test_eli[discretize]), index=X_test_eli.index)
X_test_dis=X_test_eli.drop(discretize, axis=1)
X_test_dis=pd.concat([X_test_dis, r], axis=1)
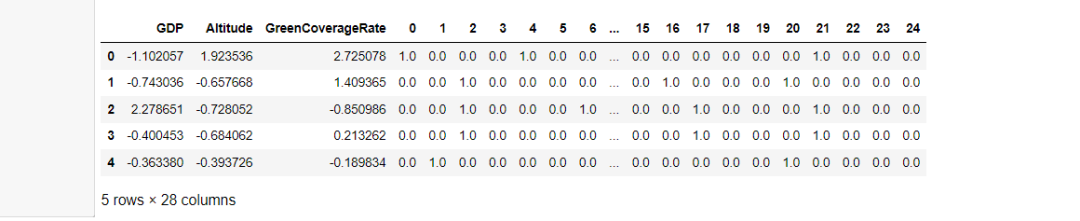
#查看转换之后的格式。
display(X_train_dis.head()
#训练模型
lr.fit(X_train_dis, y_train)
#去除异常值后评估模型效果
print(lr.score(X_train_dis, y_train))
print(lr.score(X_test_dis, y_test))
结论:离散化后模型效果进一步提升

声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
跪求各路大神labview如何计算AQI2025-05-19 6079
-
电磁轨迹预测分析系统2024-06-25 1023
-
AQI空气质量监测站——保护空气质量的重要一环2023-07-18 3732
-
AQI空气质量监测站的重要性-欧森杰2023-06-19 1186
-
预测分析介绍及行业应用案例2023-05-30 1051
-
如何改善AQI空气质量监测站的状况-欧森杰2023-05-26 1130
-
AQI分析与预测-12023-02-23 2132
-
MAX6921AQI+ PMIC - 显示驱动器2023-02-10 119
-
微型空气质量监测仪【恒美仪器HM-AQI】解决方案2021-05-19 1012
-
数据预测分析方法2016-01-15 870
-
CCD图像分析方法和预测算法???2012-07-01 2619
-
经济预测模型2011-08-15 2202
-
PCB产业投资预测分析2009-12-31 864
全部0条评论

快来发表一下你的评论吧 !

