

导航定位状态评估专题:“特征”离群点判断与剔除
描述
1、前言:
经典状态估计中协方差的计算能准确反映机器人状态的完整性吗?
在每一次机器人执行各种目的的自动导航任务时,拥有高精度且可靠状态估计的能力可以说是机器人顺利、安全完成任务的必要条件之一。简而言之,机器人状态估计算法不单单需要提供精准的状态估计量,还需要能准确地表征状态估计的准确度,比如在退化和传感器失效等场景,状态估计器能提示状态机或者用户此时刻的估计值的准确度风险,不能机器人的状态估计明显“飘”了,还在提示“一切安好”。现在回到本章节的问题:经典状态估计中协方差的计算能准确反映机器人状态的完整性吗?,该解答需要的是理解经典状态估计算法中的前提假设和模型构建。
首先,典中典的状态估计算法就是“滤波器”系列了,以扩展卡尔曼滤波器EKF为例,状态转移阶段(state evolution)的公式如下:
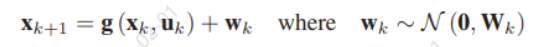
公式中右边w声明的是一个高斯白噪声,我本人理解是用该高斯白噪声表示在状态转移阶段各个系统输入量(system inputs)引入后计算所得预测结果误差,由于在实际使用过程中各个传感器性能和校验都较好,故而该高斯白噪声w是一个以0为均值的较为集中的分布。另一个就是观测模型(measurement models)的公式了:
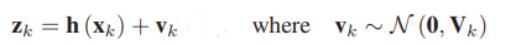
观测模型计算公式右边v声明的也是一个以0为均值的较为集中的高斯分布,本人的理解是用其表示在观测阶段各个观测数据量引入后计算所得观测结果误差。而EKF算法中的其他部分,即使在预测和观测更新的过程中利用w和v对状态量协方差进行更新与校正,其考虑的也是在传感器运行过程中正常范围内的“性能误差”引起估计值波动。由此,使用该方法计算所得的状态量协方差不能用以在退化和传感器失效等场景下机器人状态的完整性监控。
另外一个经典帧匹配算法论文:Real-Time Correlative Scan Matching(CSM帧匹配算法),该论文的主要贡献点之一就是展示了在CSM配准过程中如何获取估计协方差,换言之就是提供了一个“基于CSM方法的位姿不确定性”的判断方法。
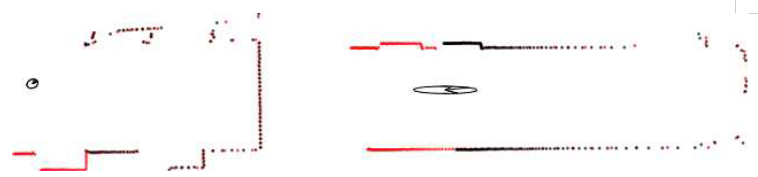
图:CSM估计的样本协方差。左:在x和y方向都有很好的约束,产生可信的协方差估计。右:长走廊只提供少数y方向纵向约束,x方向则产生一个拉长的不确定性椭圆
通过研读论文我们可以发现The Uncertainty of CSM计算模型是只考虑了“激光点云的噪声”和“激光点云与地图(Map)中corresponding cells的不确定性”,并不是考虑和分析完整环境模型(Global Map Model),故而其获取得到的估计协方差、不确定性受限于搜索窗口中的“离散采样点”,即使Map Model中存在很多“高概率”的cells,倘若这些cells不能被“离散采样点”构成的搜索窗口包含,则无法反映到The Uncertainty of CSM的计算中。所以,论文作者也提到如若想基于CSM方法来计算其位姿估计的不确定性,“离散采样点”构成的搜索窗口应该适当调整大一些(稍微大于匹配过程的搜索窗口),以保证尽可能多的将Map Model加入Uncertainty计算,但如此一来,计算量会适当增加,在具体的场景中如何设置这个计算方法中的搜索窗口参数就是一个trade off了。由此,CSM算法提供了在退化场景下估计的不确定性计算,且越是准确的不确定性表征值背后是越大的计算消耗,但CSM算法仍未针对传感器失效场景下为机器人状态的完整性监控提供相应的解决策略。
2、影响定位精度和安全的条件分析
考虑到篇幅和文章的主题,影响定位精度和安全的条件分析局限在离群点outliers对状态估计精度和对估计不确定性计算的影响。
以点云配准算法为例,输入初值initial-pose的扰动级别越大、相邻点云间的重叠度越差,则配准的精度和稳定性就越低;以RTK-GNSS定位为例,作业过程中天空遮挡越多、四周环境越复杂,则获取和解算出的定位信息精度和稳定性越低;以视觉SLAM技术为例,当视角变化越复杂、天气和光照变化越大,则视觉匹配的精度和稳定性越差……
前面提到拥有高精度且可靠状态估计的能力是机器人顺利、安全完成任务的必要条件之一。具体的,在精细需求的应用过程中,高精度的状态估计是机器人能顺利每一项具体精细动作的前提条件之一;在一些life- or mission- critical的应用过程中,稳定可靠的状态估计是机器人能避免在作业中造成人员损伤或物料损失的前提之一,即是通过监测导航完整性的风险概率值来保证作业“安全”,更准确地说,导航完整性的风险概率是指真实的机器人状态估计误差超出了预先设定的可接受阈值且没有任何报警发生的情景。
下文将分享本人整理的一些针对“特征”离群点判断与剔除和定位状态完整性监控相关方向的技术论文,推荐的原因是本人觉得这些论文提出的理论方法、技术方案对解决上面的问题很有帮助,也能为更深入的研究提供方向。
3、“特征”离群点判断与剔除
3.1 研究意义
该离群点判断与剔除类技术方案是受到RAIM(Receiver Autonomous Integrity Monitoring)的启发,RAIM其是针对GNSS数据的完整性监控,虽然完整性监测是GNSS应用的一个很好的发展领域,但将其应用于基于优化、滤波的移动机器人、无人机状态估计(例如激光、视觉建图定位)仍然不是一件简单的事情。首先,在大多数机器人状态估计算法中,系统依赖于特征(点云特征、视觉特征、路标点等)来提供观测测量,而不是卫星,与GNSS应用相比,观测测量量要多得多。
其次,在RAIM中,两颗卫星同时故障的情况很少见。然而,对于机器人状态估计,不正确测量(传感器失效)的绝对数量或异常值(离群观测量)要高得多,异常值比率通常可以大于10%。因此,需要一种不同的离群点排除方法来处理多个离群点。此外,在GNSS应用中,每个卫星提供一个测量值,但在机器人状态估计中,每个特征可能为定位轨迹中关键帧提供2或3个观测测量值。
3.2 相关技术论文
以上提及的相关技术延申到机器人状态估计的问题仅是一部分,多年来针对此类问题提出解决策略的技术论文也有很多,如下:
1. W. Ochieng, K. Sheridan, K. Sauer, X. Han, P. Cross, S. Lannelongue, N. Ammour, and K. Petit, “An assessment of the raim performance of a combined galileo/gps navigation system using the marginally detectable errors (mde) algorithm,” GPS Solutions, vol. 5, no. 3, pp. 42–51, 2002.
2. C. H. Tong and T. D. Barfoot, “Batch heterogeneous outlier rejection for feature-poor slam,” in 2011 IEEE International Conference on Robotics and Automation. IEEE, 2011, pp. 2630–2637.
3. A. Das and S. L. Waslander, “Outlier rejection for visual odometry using parity space methods,” in 2014 IEEE International Conference on Robotics and Automation (ICRA)。 IEEE, 2014, pp. 3613–3618.
4. M. A. Fischler and R. C. Bolles, “Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography,” Communications of the ACM, vol. 24, no. 6, pp. 381–395, 1981.
5. B. Kitt, A. Geiger, and H. Lategahn, “Visual odometry based on stereo image sequences with ransac-based outlier rejection scheme,” in 2010 IEEE intelligent vehicles symposium. IEEE, 2010, pp. 486–492.
6. V. Tzoumas, P. Antonante, and L. Carlone, “Outlier-robust spatial perception: Hardness, general-purpose algorithms, and guarantees,” arXiv preprint arXiv:1903.11683, 2019.
7. Mu, He-Qing, and Ka-Veng Yuen. “Novel Outlier-Resistant Extended Kalman Filter for Robust Online Structural Identification.” Journal of Engineering Mechanics, vol. 141, no. 1, 2015.
8. I. E. Potter and M. C. Sunman, “Threshold-less redundancy management with arrays of skewed instruments,” AGARD, Tech. Rep. AGARDOGRAPH-224 (pp 15-25), 1977.
9. F. Gustafsson, “Statistical signal processing approaches to fault detection,” Annual Reviews in Control, vol. 31, no. 1, pp. 41–54, 2007.
10. F. Gustafsson and F. Gustafsson, Adaptive filtering and change detection. Wiley Londres, 2000, vol. 1.
11. D. Borrmann, J. Elseberg, K. Lingemann, A. Nuchter, and J. Hertzberg, “Globally consistent 3D mapping with scan matching,” Robotics and Autonomous Systems, vol. 56, no. 2, pp. 130–142, February 2008.
12. Huang, Feng, et al. “A Coarse-to-Fine Lidar-Based Slam with Dynamic Object Removal in Dense Urban Areas.” Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), 2021.
13. Wen, Weisong, et al. “Integrity Monitoring for GNSS Positioning via Factor Graph Optimization in Urban Canyons.” Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), 2021.
14. Li, Chengyao, and Steven L. Waslander. “Visual Measurement Integrity Monitoring for UAV Localization.” 2019 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), 2019.
3.3 部分论文摘要
注:本小节选取仅仅是个人觉得对理解该类研究很有帮助的论文,并不是对上述论文做任何的质量评价和重要性评估等主观排名行为。
针对No.14 Visual Measurement Integrity Monitoring for UAV Localization, 作者在文中首要定义和讨论了如何检测出outliers并剔除的算法(I.P.S.O.R)及其相关的Protection Level,其次定义了R.B.T Metric,该metric用于定量评估“误差上界”的设计、选择估计计算的效果与合理性,最后在文中讨论了如何去计算出一个大致的误差上界(error bound),Visual Measurement Integrity Monitoring for UAV Localization这篇论文发布的年份较新,可以说其中提出来的技术方案是博采众长,美中不足的是具体的理论推导不够细腻。
针对No.3 Outlier rejection for visual odometry using parity space methods,论文作者就较为原理性地说明和推导了Parity Space是如何生成的,该Parity Space的概念也是被No.14 Visual Measurement Integrity Monitoring for UAV Localization参考并优化设计,再者就是作者给出了fault vector的选取示例,帮助理解fault vector在机器人状态估计模型中的作用,最后提出PI-RANSAC的算法来进行离群点的剔除,该算法可以与上面的I.P.S.O.R算法进行对比分析以助于相互理解。
再根据No.2 Batch heterogeneous outlier rejection for feature-poor slam,虽然这篇论文针对的feature-poor的场景,但是在当时该论文提出了较为“新颖”地使用了批量分块(Batch)处理思想,并且详细地对比了三种设计下的剔除效果:第一个测试单独使用测量模型,第二个测试将不确定度纳入假设模型,第三个测试将不确定度纳入假设模型并测量数据作为一个批量分块考虑。
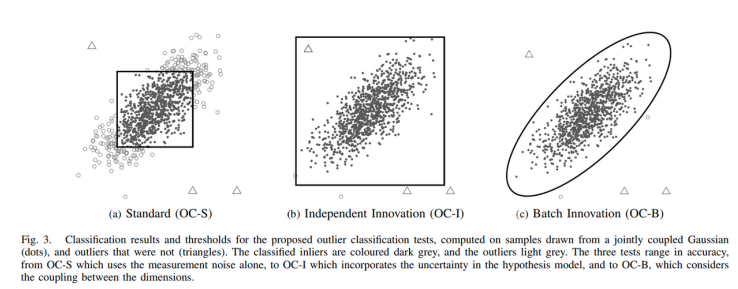
No.2在论文中提到尽管在第二种检验中考虑了假设模型的不确定性,但它仍然是真实噪声模型的近似值,因为它假设估计误差之间独立,导致计算出的error bound不能有效地反映真实的数据分布情况。虽然测量值可能是独立获得的,但估计的误差都是基于一个共同的假设模型,这个共同的基础将值连接在一起,提供了估计误差之间的相关性。由此No.2 Batch heterogeneous outlier rejection for feature-poor slam证明了在离群点判断和剔除过程中不仅需要考虑机器人模型的不确定性,还最好利用批量分块的观测数据作为一个处理单元进行分析。而这个关键的思想基本上被后续所有的论文所引用并优化升级。
4、 定位状态完整性监控
4.1 研究意义
通过上述的离群点判断和滤除算法,在数据被使用前就可以将不正确或者异常数据完成过滤,那么数据被利用在机器人状态估计的预测或者观测更新阶段时,就是可以放心使用的了。但在每个时刻的后验状态估计该怎么进行不确定性评价呢?这就需要一个有效监测移动机器人定位安全的方法了。
定位安全可通过测量机器人状态系统的完整性风险来量化的,这是一个著名的航空性能指标(aviation performance metric)。然而,航空完整性监测解决方案几乎完全依赖于全球卫星导航系统(GNSS),而机器人导航通常需要状态演化模型和/或相对定位传感器提供的额外信息,这使得先前建立的方法不切实际。那么如何设计一类适用于基于优化、滤波的移动机器人、无人机状态估计(例如激光、视觉建图定位)的高效完整性监测方法成为了亟待解决的问题。
4.2 相关技术论文
多年来针对此类问题提出解决策略的技术论文也有很多,如下:
1. G. D. Arana, M. Joerger, and M. Spenko, “Efficient integrity monitoring for kf-based localization,” in 2019 IEEE International Conference on Robotics and Automation (ICRA)。 IEEE, 2019, pp. 6374–6380.
2. G. D. Arana, O. A. Hafez, M. Joerger, and M. Spenko, “Recursive integrity monitoring for mobile robot localization safety,” in 2019 IEEE International Conference on Robotics and Automation (ICRA)。 IEEE, 2019, pp. 305–311.
3. S. Ahn, S. Yoon, S. Hyung, N. Kwak, and K. S. Roh, “On-board odometry estimation for 3d vision-based slam of humanoid robot,” in 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2012, pp. 4006–4012.
4. G. Huang, M. Kaess, and J. J. Leonard, “Towards consistent visualinertial navigation,” in 2014 IEEE International Conference on Robotics and Automation (ICRA)。 IEEE, 2014, pp. 4926–4933.
5. M. Joerger, M. Jamoom, M. Spenko, and B. Pervan, “Integrity of laser-based feature extraction and data association,” in 2016 IEEE/ION PLANS, April 2016, pp. 557–571.
6. M. Joerger, G. D. Arana, M. Spenko, and B. Pervan, “A new approach to unwanted-object detection in gnss/lidar-based navigation,” in Sensors, 2018.
7. G. D. Arana, M. Joerger, and M. Spenko, “Local nearest neighbor integrity risk evaluation for robot navigation,” ICRA, 2018.
8. M. Joerger and B. Pervan, “Kalman Filter-Based Integrity Monitoring Against Sensor Faults,” AIAA Journal of Guidance, Control and Dynamics, vol. 36, no. 2, pp. 349–361, 2013.
9. C. Tanil, M. Joerger, S. Khanafseh, and B. Pervan, “Sequential integrity monitoring for kalman filter innovation-based detectors,” ION-GNNS [accepted for publication], 2018.
10. A. Hassani, G. D. Arana, M. Spenko, and M. Joerger, “Lidar data association risk reduction using tight integration with ins,” ION-GNNS, 2018.
10. Wen, Weisong, and Li-Ta Hsu. “Towards Robust GNSS Positioning and Real-Time Kinematic Using Factor Graph Optimization.” 2021 IEEE International Conference on Robotics and Automation (ICRA), 2021.
4.3 部分论文摘要
注:本小节选取仅仅是个人觉得对理解该类研究很有帮助的论文,并不是对上述论文做任何的质量评价和重要性评估等主观排名行为。
上面论文列表中的No.1 Efficient integrity monitoring for kf-based localization和No.2 Recursive integrity monitoring for mobile robot localization safety是由同一位研究学者Guillermo Duenas Arana及其团队完成的,其较为充分地提出了可以有效应用在基于滤波的机器人状态估计中的完整性监测算法(Localization Integrity Monitoring)。论文分析到卡尔曼滤波器(KF)提供的是一种递归解决的方案,该解决方案采用的是关于先验估计和状态演化模型的信息和/或其他类型的相对定位传感器信息,在设计评估KF解决方案时的完整性风险时,首先需要将当前时刻之前发生的故障封装成估计偏差,然后通过将先前的状态估计作为额外的测量,将KF更新方程重新表述为最小二乘拟合问题。根据该公式,使用传统的航空RAIM算法评估定位完整性。论文提出的算法允许在一个公共框架内有效监测当前和以前的传感器故障。虽然这种方法在应用于测量源有限的任务时可能有显著的缺点,但它具有实际的好处,特别是对于低计算能力的系统。
再进一步概况,No.1 Efficient integrity monitoring for kf-based localization和No.2 Recursive integrity monitoring for mobile robot localization safety的主要贡献先是定义了Hazardous Misleading Information(HMI)的概念并提供了计算方法,在具体fault vector和estimate error的分布估计时简单阐明了具体示例中fault detector该如何使用,其本质上还是基于卡方分布完成对statistic test的分析。特别是No.2 Recursive integrity monitoring for mobile robot localization safety,该论文有很详细的理论推导,细致地展示fault vector该如何设计和推到求解,与No.1论文相互对比和分析后,可实现相关理论的举一反三。
5、总结与延申
在“特征”离群值的判断与剔除算法机制的帮助下可以在一定程度上规避垃圾观测数据和传感器失效引发的机器人状态估计错误问题,同时机器人状态完整性监控算法可为帮助机器人能准确地表征其状态估计量的准确值,以帮助机器人在传感器退化和传感器失效等场景下及时完成导航、定位策略的切换和多传感器观测模型的深度融合。
另一方面,“特征”离群值的判断与剔除算法和机器人状态完整性监控算法也为全生命周期建图定位系统Life-long SLAM的稳定实现提供了基础。“特征”离群值的判断与剔除算法可以帮助克服Life-long对视角变化,天气变化,光照变化条件下,以及动态障碍物环境下,如何确保定位和建模的精度的核心问题,而机器人状态完整性监控算法则辅助保证Life-long过程中约束构建的准确性,当Life-long过程中的环境发生变化之后,通过完整性监控可以避免匹配约束构建后的歧义,即是可以通过完整性监控获取得到的匹配约束准确度,从而对“较差”的约束进行其他处理。
审核编辑 :李倩
-
影像仪全景导航,快速定位产品特征!2023-11-20 1004
-
导航定位技术分类2021-09-01 1584
-
高阶多视图离群点检测及其研究综述2021-05-07 936
-
惯性导航模块特征和 优势有哪些?2020-08-13 2298
-
详谈车载导航定位技术的概述和测试方法2020-07-10 1202
-
卫星导航定位天线有哪些类别?2019-08-15 4317
-
车载终端的导航定位标准以及导航定位射频性能测试系统和测试项目介绍2019-07-11 4106
-
一种散乱点云近离群点的识别算法2018-01-12 602
-
基于CCA的SIFT误匹配剔除方法2017-12-29 1220
-
局部密度离群点检测算法2017-11-25 751
-
基于数据集对象平均离群因子的离群点选择算法2017-01-03 684
-
【专题制作】GPS定位导航方案_GPS注意事项精华大全2016-08-05 3860
-
汽车电子GPS导航定位主要作用有四点2012-10-23 3958
-
车载组合导航定位系统误差建模及仿真2009-12-14 719
全部0条评论

快来发表一下你的评论吧 !

