MATLAB学习笔记之PID算法2
电子说
1.3w人已加入
描述
2.4.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
float umax ; //积分上限
float umin ; //积分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( abs(pid.err)<= pid.umax )
{
index = 1 ;
pid.integral += pid.err ;
}
else
index = 0 ;
pid.voltage = pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*( pid.err-pid.err_last ) ;
pid.err_last = pid.err ;
pid.ActualSpeed = pid.voltage*1.0 ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<1000 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
printf( "%.2f\\n" , Speed ) ;
}
}
2.5 抗积分饱和型PID算法
2.5.1 实现原理
所谓积分饱和现象是指如果系统存在一个方向的偏差，PID控制器的输出会因为存在积分环节而不断累积增大，从而导致执行机构达到极限位置，若控制器输出响应继续增大，执行器开度不可能再增大，此时计算机输出控制量超出了正常运行范围而进入饱和区，一旦系统出现反向偏差，输出响应逐渐从饱和区退出，进入饱和区时间越长则退出饱和区的时间也就随之增加，这段时间里，执行机构仍然停留在极限位置而不能随着偏差方向立即作出相应的改变，造成控制性能恶化，这种现象称为积分饱和现象或积分失控现象。实现抗积分饱和算法的基本思路是计算系统的响应时，首先判断上一时刻的控制量是否超出了极限范围，如果超过上限，则只累计反向偏差，若低于下限，则只累计正向偏差，从而避免控制量长时间停留在饱和区。
2.5.2 MATLAB算法
clc
clear
%PID初始化
len = 180 ; %运算次数
y = zeros(1,len); %期望值
y_d = zeros(1,len); %过程值
err = zeros(1,len); %误差值
err_0 = 0 ; %k时刻误差
err_1 = 0 ; %k-1时刻误差
y_d_last = 0 ; %k-1时刻输出
integral = 0; %积分值
Kp = 0.2; %比例系数
Kd = 0.2; %微分值
Ki = 0.1 ; %积分值
max = 400 ; %积分上限
min = -200 ; %积分下限
index = 0 ; %积分有效性
%运算过程
for k=1:1:len
y(k) = 200 ; %期望输出
err_0 = y(k)-y_d_last; %计算偏差
if y_d_last>max
if abs(err_0) <= y(k)
index = 1 ;
if err_0 < 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
elseif y_d_last<min
if abs(err_0) <= y(k)
index = 1 ;
if err_0 > 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
else
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %误差累计
else
index = 0 ;
end
end
y_d_last = Kp*err_0 + Ki*index*integral + Kd*(err_1-err_0); %位置型PID运算公式
err_1 = err_0 ;
%更新参数
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%输出图像绘制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('输出曲线');
xlabel('t')
ylabel('y(t)')
%误差图像绘制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('误差曲线');
xlabel('t')
ylabel('e(t)')
MATLAB运行结果如下图所示。
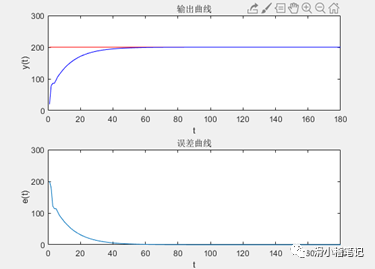
2.5.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
float umax ; //积分上限
float umin ; //积分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( pid.ActualSpeed>pid.umax )
{
if( abs(pid.err)<=200 )
{
index = 1 ;
if( pid.err<0 )
pid.integral += pid.err ;
}
else
index = 0 ;
}
else if( pid.ActualSpeed
2.6 梯形积分PID算法
2.6.1 实现原理
根据梯形算法的积分环节公式
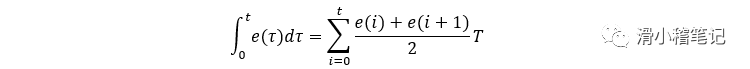
作为PID控制的积分项，其作用是消除余差，为了尽量减小余差，应提高积分项运算精度，为此可以将矩形积分改为梯形积分，具体实现的语句为pid.voltage = pid.Kppid.err+indexpid.Ki pid.integral/2+pid.Kd ( pid.err-pid.err_last ) ;
2.6.2 MATLAB算法
clc
clear
%PID初始化
len = 358 ; %运算次数
y = zeros(1,len); %期望值
y_d = zeros(1,len); %过程值
err = zeros(1,len); %误差值
err_0 = 0 ; %k时刻误差
err_1 = 0 ; %k-1时刻误差
y_d_last = 0 ; %k-1时刻输出
integral = 0; %积分值
Kp = 0.2; %比例系数
Kd = 0.2; %微分值
Ki = 0.1 ; %积分值
max = 400 ; %积分上限
min = -200 ; %积分下限
index = 0 ; %积分有效性
%运算过程
for k=1:1:len
y(k) = 200 ; %期望输出
err_0 = y(k)-y_d_last; %计算偏差
if y_d_last>max
if abs(err_0) <= y(k)
index = 1 ;
if err_0 < 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
elseif y_d_last<min
if abs(err_0) <= y(k)
index = 1 ;
if err_0 > 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
else
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %误差累计
else
index = 0 ;
end
end
y_d_last = Kp*err_0 + Ki*index*integral/2 + Kd*(err_1-err_0); %PID运算公式
err_1 = err_0 ;
%更新参数
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%输出图像绘制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('输出曲线');
xlabel('t')
ylabel('y(t)')
%误差图像绘制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('误差曲线');
xlabel('t')
ylabel('e(t)')
2.6.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
float umax ; //积分上限
float umin ; //积分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( pid.ActualSpeed>pid.umax )
{
if( abs(pid.err)<=200 )
{
index = 1 ;
if( pid.err<0 )
pid.integral += pid.err ;
}
else
index = 0 ;
}
else if( pid.ActualSpeed
声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表电子发烧友网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。
举报投诉
-
旋转倒立摆的PID算法的MATLAB仿真原理图2013-09-06 0
-
PID算法之模糊PID 精选资料推荐2021-07-19 0
-
连续控制系统的PID算法及MATLAB仿真2021-08-11 0
-
使用C语言进行PID算法实现2021-09-15 0
-
求大佬分享MatLab的学习笔记2021-11-19 0
-
PID算法学习笔记分享2022-01-14 0
-
基于遗传算法的PID 控制及其MATLAB 仿真2009-06-11 923
-
模糊PID控制及其MATLAB仿真2015-11-12 1233
-
PID算法Matlab仿真程序和C程序2015-11-20 1032
-
PID学习算法2016-06-17 518
-
OpenStack之Cinder学习笔记2021-09-23 695
-
PID算法学习笔记2022-01-14 464
-
MATLAB学习笔记之PID算法32023-02-24 1990
-
MATLAB如何实现PID？2023-11-04 2788
全部0条评论
快来发表一下你的评论吧 !
