

MATLAB学习笔记之PID算法3
电子说
描述
2.7 变积分PID算法
2.7.1 实现原理
变积分PID可以看做是积分分离的PID算法的更一般形式,在普通的PID控制算法中,由于积分系数是常数,所以在整个控制过程中,积分增量是不变的,但是,系统对于积分项的要求是,系统偏差较大时,积分作用应该减弱甚至全无,而在偏差较小时,则应该加强,积分系数取大了会引起超调,甚至积分饱和,取小了又不能短时间内消除静差,因此,需要根据系统偏差的大小改变积分速度。
变积分PID的基本思想是改变积分项的累加速度,使其与偏差大小相对应,偏差越大,积分越慢,偏差较小,积分越快。
这里给积分系数前加一个比例系数index,使最终的比例环节的积分系数为Ki*index。
2.7.1 MATLAB算法
clc
clear
%PID初始化
len = 200 ; %运算次数
y = zeros(1,len); %期望值
y_d = zeros(1,len); %过程值
err = zeros(1,len); %误差值
err_0 = 0 ; %k时刻误差
err_1 = 0 ; %k-1时刻误差
y_d_last = 0 ; %k-1时刻输出
integral = 0; %积分值
Kp = 0.4; %比例系数
Kd = 0.2; %微分值
Ki = 0.2 ; %积分值
max = 400 ; %积分上限
min = -200 ; %积分下限
index = 0 ; %积分有效性
%运算过程
for k=1:1:len
y(k) = 200 ; %期望输出
err_0 = y(k)-y_d_last; %计算偏差
if abs(err_0) > max
index = 0 ;
elseif abs(err_0) < min
index = 1 ;
integral = integral+err_0; %误差累计
else
index = ( max-abs(err_0) )/20 ;
integral = integral+err_0; %误差累计
end
y_d_last = Kp*err_0 + Ki*index*integral/2 + Kd*(err_1-err_0); %PID运算公式
err_1 = err_0 ;
%更新参数
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%输出图像绘制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('输出曲线');
xlabel('t')
ylabel('y(t)')
%误差图像绘制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('误差曲线');
xlabel('t')
ylabel('e(t)')
2.7.2 C算法
#include
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.4 ;
pid.Kd = 0.2 ;
pid.Ki = 0.2 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( abs(pid.err)>200 )
index = 0 ;
else if( abs(pid.err)<180 )
{
index = 1 ;
pid.integral += pid.err ;
}
else
{
index = ( 200-abs(pid.err) )/20 ;
pid.integral += pid.err ;
}
pid.voltage = pid.Kp*pid.err+index*pid.Ki*pid.integral/2+pid.Kd*( pid.err-pid.err_last ) ;
pid.err_last = pid.err ;
pid.ActualSpeed = pid.voltage*1.0 ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<150 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
printf( "%.2f\\n" , Speed ) ;
}
}
2.8 专家PID与模糊PID算法思想
PID的控制思想非常简单,主要就是比例,积分和微分环节的参数整定过程,对于执行期控制模型确定或者控制模型简单的系统来说,参数的整定可以通过计算获得,对于一般精度要求不是很高的执行器系统,可以采用拼凑的方法进行实验型的整定。
但是,实际的系统大部分属于非线性系统,或者说是系统模型不确定的系统,如果控制精度要求较高的话,那么对于参数的整定过程也是有难度的,专家PID和模糊PID就是为了满足这方面的需求而设计的,专家算法和模糊算法都归属于智能算法的范畴,智能算法最大的优点就是在控制模型未知的情况下,可以对模型进行控制,这里需要注意的是,专家PID也好,模糊PID也好,绝对不是专家系统或模糊算大与PID控制算法的简单加和,它是专家系统或者模糊算法在PID控制器参数整定上的应用,也就是说,智能算法是辅助PID进行参数整定的手段。
关于专家PID的C语言实现,需要找到一些依据,还需要从PID系数本身考虑。
1、比例系数Kp的作用是加快系统的响应速度,提高系统的调节精度,Kp越大,系统的响应速度越快,调节的精度越高,但是容易产生超调,甚至会引起系统不稳定,Kp取值过小,则会降低系统的调节精度,拖慢响应速度,从而延长调节时间,使系统的静态,动态特性变差。
2、积分系数Ki的作用是消除系统的稳态误差,Ki越大,系统的静态误差消除得越快,但是若Ki过大,在响应过程的初期就会产生积分饱和的现象,从而引起相应过程的较大超调,若Ki过小,将使系统静态误差难以消除,影像系统的调节精度。
3、微分系数Kd的作用是改善系统的动态特性,其作用主要是在响应过程中抑制偏差向任何方向的变化,对偏差变化进行提前预报,但是若Kd过大,会使响应过程提前制动,从而延长调节时间,而且会降低系统的抗干扰性。

2.9 PID算法应用——电机转速控制
PID是一种广泛应用在控制理论中的算法,以直流电机为例,要想精确控制电机的转速就需要形成一种闭环控制思想。首先将一个默认的输入端的电压值发送给直流电机,通过转速传感器将当前电机的转速反馈到输入端,通过与输入端做运算,如果转速高于设定的值,则减小输入端电压,如果转速低于设定的值,则提高输入端电压,由此形成了一种闭环控制回路,即通过不停的对输出端进行反馈,以达到精确控制的目的。为了使控制系统的速度更快,精确性更高,稳定性更强,PID控制器被广泛应用在了这里面,现在我们通过MATLAB的Simulink来实现直流电机的PID控制。
一个直流电机的模型如上图所示,为了简化讨论,假设转子和转轴都是刚体,且转子受到的磁场恒定,转子收到的摩擦力与速度成正比,该电机的物理参数为:
(1)转子的转动惯量J=0.01kg·m^2^
(2)电机摩擦系数b=0.01N···m·s
(3)电动势常数Ke=0.01V/rad/sec
(4)电机扭矩常数Kt=0.01N·m/Amp
(5)电阻R=1Ω
(6)电感L=0.5H

我们希望控制器输入1V电压的时候稳定状态下保持0.1rad/sec的转速,稳定时间2s,稳态误差低于1%,受到阶跃输入干扰的时候超调小于5%。Matlab的仿真并不像之前学习51的时候用的Protuse一样,可以看到直观效果,Matlab的仿真实际是对数学的计算过程,即输入与输出必须都抽象成函数表达式进行,通过观察输出的函数表达式与波形来判断系统的工作状态与性能。我们将上面得到的复频域下的函数表达式代入参数,得到
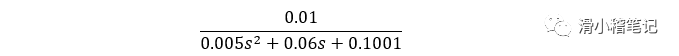
通过Simulink创建仿真图如下图所示。

双击PID控制器的图标,打开了以下对话框。
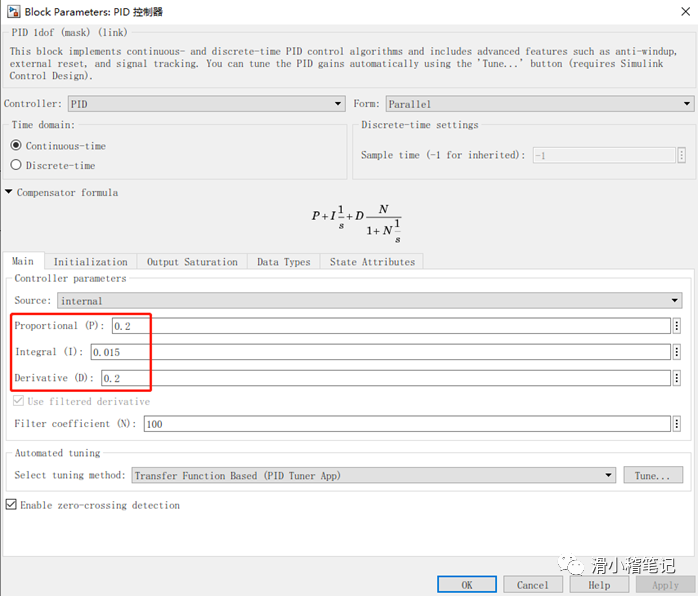
对话框内的这三个参数就是PID控制器的三个参数,其中Proportional代表比例环节,Integral代表积分环节,Derivative代表微分环节,通过修改这三个参数达到实现控制系统的目的。
在PID控制中,这三个参数分别对系统控制有以下几个作用:
(1)比例环节P:控制输出响应的速度,减小稳态误差,但是会增大超调量
(2)积分环节I:消除系统的稳态误差,加快达到稳定所需的时间,但也会增大超调量
(3)微分环节D:加快动态过程,容易引起系统震荡,同样,微分环节也会增大超调量
为了满足:
(1)稳定时间2s
(2)稳态误差低于1%
(3)超调小于5%
这三个条件,我们首先修改比例环节,用来满足稳态误差低于1%这个参数。通过实验发现,当比例环节设定在100以上的时候,稳态误差低于1%,如下图所示。
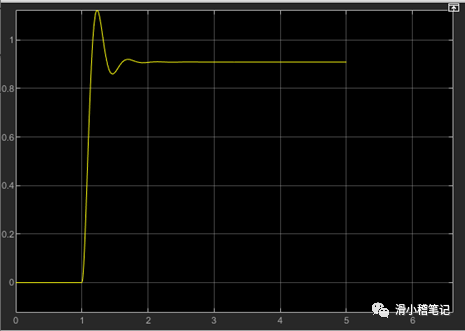
但是我们发现
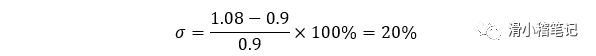
即系统的超调量较大,达到了20%,此时需要调节微分环节达到目的,我们通过实验发现,当微分环节超过10时,系统的超调如下图所示。
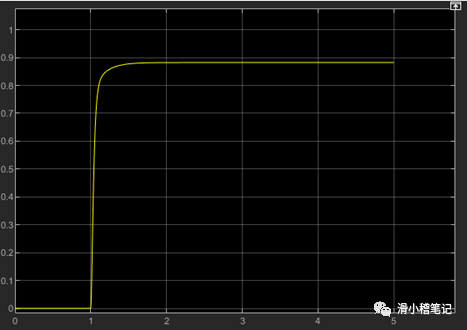
此时系统已经不存在超调,现在只需要解决稳定时间小于2s这个参数即可,我们通过设置积分环节达到这个目的,通过实验发现,当系统的积分环节大于200时,稳定时间小于2s。
-
PID控制算法学习笔记资料2025-08-12 952
-
MATLAB学习笔记之PID算法22023-02-24 1206
-
PID算法学习笔记分享2022-01-14 904
-
求大佬分享MatLab的学习笔记2021-11-19 1288
-
OpenStack之Cinder学习笔记2021-09-23 880
-
使用C语言进行PID算法实现2021-09-15 1860
-
连续控制系统的PID算法及MATLAB仿真2021-08-11 5061
-
【专辑精选】PID算法学习书籍资料汇总2019-05-30 5661
-
PID学习算法2016-06-17 576
-
PID算法Matlab仿真程序和C程序2015-11-20 1175
-
模糊PID控制及其MATLAB仿真2015-11-12 1380
-
旋转倒立摆的PID算法的MATLAB仿真原理图2013-09-06 10252
-
基于遗传算法的PID 控制及其MATLAB 仿真2009-06-11 1018
全部0条评论

快来发表一下你的评论吧 !

