如何构建神经网络

 

 

一.项目背景
 

    神经网络是模拟人体生物神经元原理构建的，比较基础的有M-P模型，它按照生物
神经元的结构和工作原理构造出来的一个抽象和简化的模型。简单来说，他是对一个生
物神经元建模，下图是一个M-P模型示意图。

 

•  
•  
•  

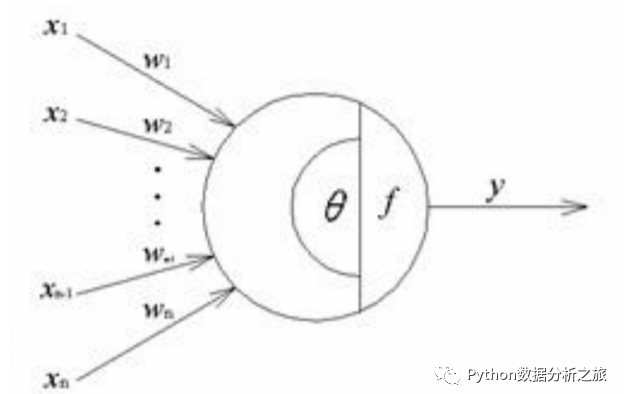
    跟人体生物神经元类似，神经元激活与否取决于某一阈值电平，即只有大当其总和阈值θ
时，神经元才会被激活而发放脉冲，否则整个神经元不会发生输出信号。整个过程用下面函数
来表示。

 

•  
•  
•  

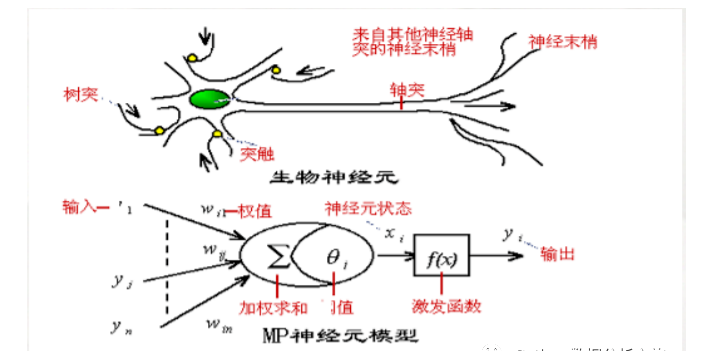
   上图中f我们称为激活函数，常见的激活函数可以分为两种类型，线性与非线性函数，具体见下图。
常用激活函数有S形函数，双曲正切函数等,后期我们会讲到。对于M-P模型而言，神经元只有兴奋和抑
制状态，因此这里的激活函数定义为单位阶跃函数，输出y只有0和1两种信号

 

二.搭建网络

 

 

•  

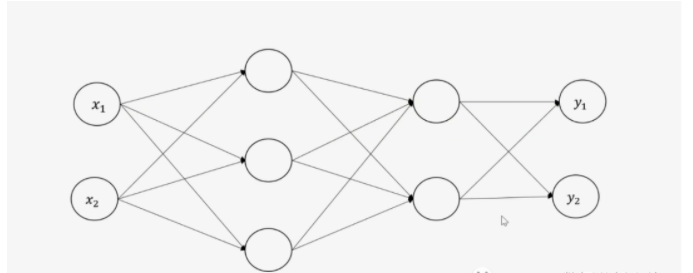
该网络含有一个输入层，两个隐藏层和一个输出层的神经网络，接下来我们手动实现它。

 

import numpy as np

#定义Sigmod激活函数
def sigmod(z):
    return 1/(1+np.exp(-z))

#Z1=X*W1+b1,A1=sigmod(Z1)

#输入数据，形状为(1,2)
X=np.array([
    [0.1,0.5]
])

#(2,3)
W1=np.array([
    [0.1,0.3,0.5],
    [0.2,0.4,0.6]
])

#(1,3)
b1=np.array([
    [0.1,0.2,0.3]
])

#进行线性运算
Z1=np.dot(X,W1)+b1
#经过sigmod激活函数，将线性函数转换为非线性函数
A1=sigmod(Z1)

print('Z1 shape',Z1.shape)
print('A1 shape',A1.shape)

 

#第2层
#Z2=W2*A1+b2，A2=sigmod(Z2)

#(3,2)
W2=np.array([
    [0.1,0.2],
    [0.3,0.4],
    [0.5,0.6]
])

#(1,2)
b2=np.array([[0.1,0.2]])
#进行线性运算
Z2=np.dot(A1,W2)+b2
#经过sigmod激活函数，将线性函数转换为非线性函数
A2=sigmod(Z2)

print('Z2 shape',Z2.shape)
print('A2 shape',A2.shape)

 

#第3层
#Z3=W3*A2+b3，A3=sigmod(Z3)

#(2,2)
W3=np.array([
    [0.1,0.3],
    [0.2,0.4]
])

#(1,2)
b3=np.array([[0.1,0.2]])
#线性运算
Z3=np.dot(A2,W3)+b3
#输出Y
Y=sigmod(Z3)
#表示一个样本两个输出值
Y