高速模数转换器的INL/DNL测量

虽然积分和微分非线性可能不是高速、高动态性能数据转换器最重要的参数，但在高分辨率成像应用中，它们变得越来越重要。以下应用笔记可作为其定义的复习课程，详细介绍了高速模数转换器（ADC）中测量INL和DNL的两种不同但常用的技术。

制造商推出的高性能模数转换器（ADC），具有出色的静态和动态性能。您可能会问，“他们如何衡量这种性能，使用什么设备？以下讨论应阐明测试对ADC重要的两个精度参数的技术：积分非线性（INL）和微分非线性（DNL）。

虽然INL和DNL不是指定通信和快速数据采集应用中使用的高性能数据转换器的最重要电气特性之一，但它们在更高分辨率的成像应用中具有重要意义。但是，除非您经常使用ADC，否则很容易忘记这些参数的确切定义和重要性。因此，下一节将作为简短的进修课程。

INL 和 DNL 定义

DNL误差定义为实际步宽与1LSB理想值之间的差值（见图1a）。对于差分非线性度与DNL = 0LSB一致的理想ADC，每个模拟步进等于1LSB （1LSB = VFSR/2N，其中 VFSR是满量程范围，N是ADC的分辨率），转换值相距正好1LSB。小于或等于 1LSB 的 DNL 误差规范保证了没有失码的单调传递函数。当ADC的数字输出随着输入信号的增加而增加（或保持不变）时，ADC的单调性得到保证，从而避免了传输曲线斜率的符号变化。DNL 在消除静态增益误差后指定。它的定义如下：

DNL = |[(VD+1- VD)/VLSB-IDEAL - 1] | , where 0 < D < 2N - 2.

VD是数字输出代码D对应的物理值，N是ADC分辨率，V是LSB-理想是两个相邻数字代码的理想间距。通过添加超出量化影响的噪声和杂散分量，较高的DNL值通常会限制ADC在信噪比（SNR）和无杂散动态范围（SFDR）方面的性能。

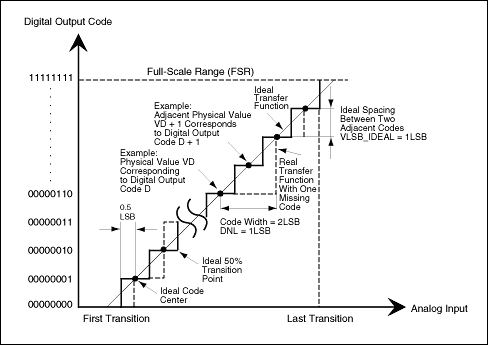
图 1a.为了保证无失码和单调传递函数，ADC的DNL必须小于1LSB。

INL误差被描述为实际传递函数与直线的偏差，以LSB或满量程范围（FSR）的百分比为单位。然后，INL误差幅度直接取决于为这条直线选择的位置。至少有两个定义是通用的：“最佳直线INL”和“终点INL”（见图1b）：

最佳直线INL提供有关偏移（截距）和增益（斜率）误差的信息，以及传递函数的位置（如下所述）。它以直线的形式确定最接近ADC实际传递函数的近似值。线的确切位置没有明确定义，但这种方法产生了最佳的可重复性，并且可以作为线性度的真实表示。

端点INL将直线穿过转换器传递函数的端点，从而定义线路的精确位置。因此，N位ADC的直线由其零（全零）和满量程（全1）输出定义。

通常首选最佳直线方法，因为它会产生更好的结果。INL规范是在静态失调和增益误差均无效后测量的，可以描述如下：

INL = | [(VD - VZERO)/VLSB-IDEAL] - D | , where 0 < D < 2N-1.

VD是数字输出代码D表示的模拟值，N是ADC的分辨率，V零是对应于全零输出代码的最小模拟输入，并且 VLSB-理想是两个相邻输出代码的理想间距。

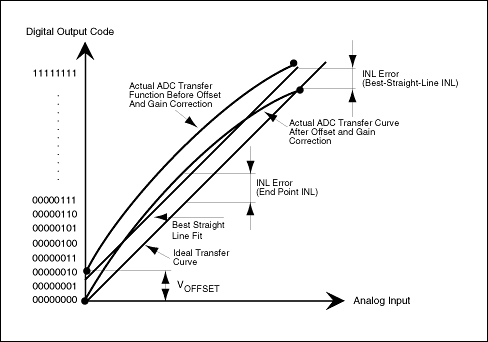
图 1b.最佳直线和端点拟合是定义ADC线性度特性的两种可能方法。

传递函数

理想ADC的传递函数是一个阶梯，其中每个胎面代表一个特定的数字输出代码，每个立管代表相邻代码之间的转换。必须定位与这些转换相对应的输入电压，以指定ADC的许多性能参数。这项工作可能很复杂，特别是对于高速转换器中的噪声转换以及接近最终结果且变化缓慢的数字代码。

如图1b所示，转换没有明确定义，但更现实地表示为概率函数。随着缓慢增加的输入电压通过转换，ADC越来越频繁地转换为下一个相邻代码。根据定义，转换对应于ADC以相等概率转换为每个侧翼代码的输入电压。

正确的过渡

转换电压定义为产生两个相邻代码之一的概率相等的输入电压。标称模拟值对应于模拟输入在一对相邻转换之间的范围内生成的数字输出代码，定义为该范围的中点（50%点）。如果转换间隔的极限已知，则可以轻松计算出这 50% 的点。在测试中，可以通过测量转移间隔的限制来确定转换点，然后将间隔除以每个相邻代码在其中出现的次数。

用于测试静态 INL 和 DNL 的通用设置

INL和DNL可以使用准直流电压斜坡或低频正弦波作为输入进行测量。简单的直流（斜坡）测试可以包含逻辑分析仪、高精度DAC（可选）、用于扫描被测器件（DUT）输入范围的高精度直流电源，以及附近PC或X-Y绘图仪的控制接口。

如果设置包括高精度DAC（远高于DUT的DAC），则逻辑分析仪可以通过直接处理ADC的输出数据来监控失调和增益误差。精密信号源通过从零电平到满量程缓慢扫描ADC的输入范围，为DUT产生测试电压。一旦由DAC重建，ADC输入端的每个测试电压将从DAC输出端的相应直流电平中减去，从而产生很小的电压差（V差异），可以用 X-Y 绘图仪显示并链接到 INL 和 DNL 错误。量化水平的变化表明微分非线性，V的偏差差异从零开始表示存在积分非线性。

模拟积分伺服回路

确定ADC静态线性度参数的另一种方法（与前面类似，但更为复杂）是使用模拟积分伺服环路。此方法通常用于专注于高精度测量而不是速度的测试设置。

典型的模拟伺服环路（见图2）由一个积分器和两个连接到ADC输入的电流源组成。一个电源强制电流进入积分器，另一个电源用作吸电流。连接到ADC输出的数字幅度比较器控制两个电流源。幅度比较器的另一个输入由PC控制，PC将其扫描通过2N- 1 N位转换器的测试代码。

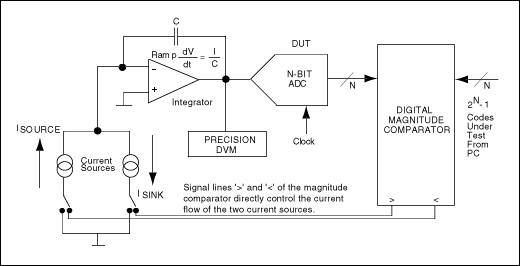
图2.该电路配置为模拟积分伺服回路。

如果环路周围反馈的极性正确，幅度比较器会使电流源在给定代码转换周围伺服模拟输入。理想情况下，此操作会在模拟输入端产生一个小的三角波。幅度比较器控制这些斜坡的速率和方向。积分器的斜坡速率在接近过渡时必须很快，但在使用精密数字电压表（DVM）测量时，积分器的斜坡速率必须足够慢，以最大限度地减少叠加三角波的峰值偏移。

对于MAX108上的INL/DNL测试，伺服环板通过两个接头连接到评估板（见图3）。一个接头在MAX108的主（或辅助）输出端口和幅度比较器的可锁存输入端口（P）之间建立连接。第二个接头确保伺服回路（幅度比较器的Q端口）与计算机生成的数字参考代码之间的连接。

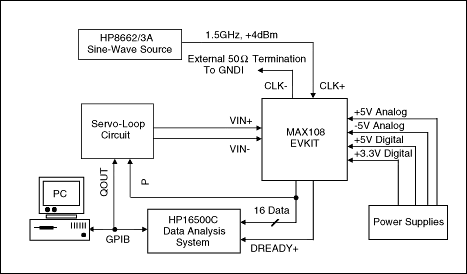
图3.借助MAX108评估板和模拟积分伺服环路，该测试设置确定MAX108的INL和DNL特性。

通过这种比较得出的完全解码决策可在比较器输出P>QOUT上获得，然后传递给积分器配置。每个比较器结果独立控制开关的逻辑输入，并根据需要生成电压斜坡，以驱动DUT两个输入的后续积分器电路。这种方法有其优点，但也有几个缺点：

三角斜坡应具有低dV/dt，以最大限度地降低噪声。这种情况会产生可重复的数字，但它会导致精密仪表的积分时间较长。

正负斜坡速率必须匹配以达到50%点，并且必须平均低电平三角波以达到所需的直流电平。

积分器设计通常需要仔细选择电荷电容器。例如，为了尽量减少由于电容器的“记忆效应”而导致的潜在误差，请选择具有低介电吸收的积分器电容器。

精度与积分周期成正比，与建立时间成反比。

连接到模拟集成伺服回路测量的DVM INL/DNL 错误与输出代码的关系（图 4a 和 4b）。请注意，“INL 与输出代码”图中的抛物线或弓形表示 偶次谐波占主导地位，“S 形”表示 奇次谐波占主导地位。

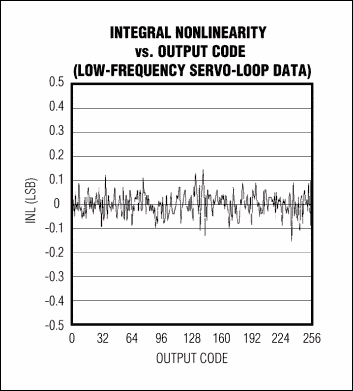
图 4a.该图显示了MAX108 ADC的典型积分非线性度，通过模拟积分伺服环路捕获。

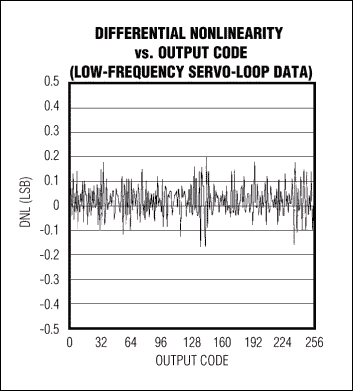
图 4b.该图显示了MAX108的典型差分非线性，通过模拟积分伺服环路捕获。

为了消除先前方法中的负面影响，您可以将伺服环路的积分器部分替换为捕获DUT输出代码的L位逐次逼近寄存器（SAR）、L位DAC和简单的平均电路。该电路与幅度比较器一起构成SAR型转换器配置（参见图5和下文“SAR转换器”讨论），其中幅度比较器对DAC进行编程，读取其输出，并执行逐次逼近。同时，DAC为被测N位ADC的输入提供高分辨率直流电平。在这种情况下，选择16位DAC将ADC调整至1/8LSB精度，并获得最佳传输曲线。

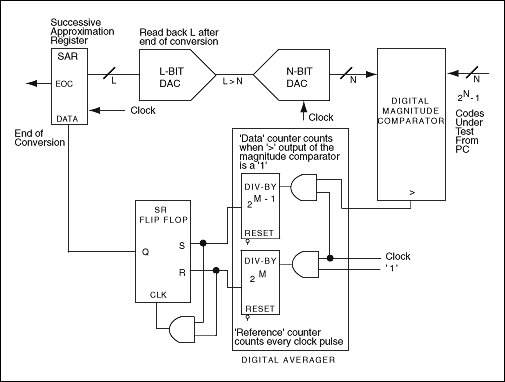
图5.逐次逼近和DAC配置取代了模拟伺服环路的积分器部分。

当噪声导致幅度比较器切换并变得不稳定时，平均电路的优势是显而易见的，就像它在接近最终结果时一样。平均电路中包括两个分频计数器。“参考”计数器的周期为 2M时钟周期，其中M是控制周期（以及测试时间）的可编程整数。“数据”计数器仅在幅度比较器输出较高时递增，其周期等于前2M-1周期。

参考和数据计数器一起平均高点和低点的数量，将结果存储在触发器中，然后将其传递到SAR寄存器。此过程重复 16 次（在本例中）以生成完整的输出代码字。与以前的方法一样，这种方法也有优点和缺点：

测试设置的输入电压以数字方式定义，允许轻松修改要平均结果的样本数量。

SAR 方法在 DUT 的模拟输入端提供直流电平，而不是斜坡。

缺点是反馈环路中的DAC对输入电压的分辨率设置了有限的限制。

SAR 转换器

SAR转换器的工作方式类似于老式化学家的天平。一边是未知输入样本，另一边是SAR/DAC配置产生的第一个权重（最高有效位，等于满量程输出的一半）。如果未知重量大于 1/2FSR，则第一个重量仍保留在天平上，并增加 1/4FSR。如果未知重量较小，则删除权重并替换为 1/4FSR 的权重。

然后，SAR转换器通过重复此过程N次来确定所需的输出代码，从MSB进展到LSB。N 是 SAR 配置中 DAC 的分辨率，每个权重代表 1 个二进制位。

INL和DNL的动态测试

为了评估ADC的动态非线性度，可以应用满量程正弦输入，并测量转换器在整个全功率输入带宽内的信噪比（SNR）。理想N位转换器（仅受量化噪声影响，无失真）的理论SNR如下：

信噪比（以分贝为单位）= N×6.02 +1.76。

此品质因数中嵌入了毛刺、积分非线性和采样时间不确定性的影响。您可以通过在恒定频率下执行 SNR 测量并作为信号幅度的函数来获得额外的线性度信息。扫描整个幅度范围，例如，从零到满量程，反之亦然，当源幅度接近转换器的满量程限值时，会产生与源信号的较大偏差。为了确定这些偏差的原因，同时排除失真和时钟不稳定的影响，请使用频谱分析仪分析量化误差信号作为频率的函数。

还有无数其他方法可用于测试高速和低速数据转换器的静态和动态INL和DNL。这里的目的是让您更好地了解使用简单但仍然智能和精确的工具和技术生成强大的 TOC（典型操作特性）。