

高速ADC的动态测试
描述
模数转换器 (ADC) 代表接收器、测试设备和其他电子设备中模拟和数字世界之间的链接。如本系列文章第1部分所述,许多关键动态参数提供了给定ADC预期动态性能的精确相关性。本系列文章的第 2 部分介绍了用于测试高速 ADC 动态规格的一些设置配置、设备建议和测量程序。
下面讨论用于测试高速数据转换器的推荐设置和步骤。它包括测试Maxim全新10位+3V高速数据转换器系列所需的软件工具、硬件配置以及数据采集和分析仪器。它还警告如果不小心执行设备选择、设置配置、布局和基于 FFT 的分析,您可能会遇到陷阱。涵盖以下主题:
动态规范和定义
主板布局和硬件配置
功率谱、箱、频谱泄漏和窗口功能
用于测试 SNR、SINAD、THD、SFDR 和 TTIMD 的软件工具
有许多方法可用于从A/D转换器(不仅仅是高速转换器)获取输出数据并分析其动态性能。这里介绍的方法代表了一种行之有效的方法,鼓励读者根据手头的应用程序进行必要的修改。
动态规格
对于那些错过了本讨论第1部分的人,以下是高速ADC重要动态参数的定义和数学描述的简要概述。
| 动态参数 | 描述/定义 |
| 信噪比 (SNR) | 信噪比 = 6.02 × N + 1.76。 |
| 信噪比和失真比 (SINAD) | 西纳德分贝= 20 ×日志10(一信号[有效值] / A噪声[有效值])。 |
| 有效位数 (ENOB) | ENOB = (SINAD - 1.76) / 6.02。 |
| 总谐波失真 (THD) |
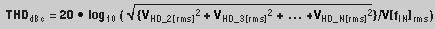 |
| 无杂散动态范围 (SFDR) | SFDR是以基波(最大信号分量)的均方根幅度与次大杂散分量的均方根值的分贝表示的比率,不包括直流偏移。 |
| 双音互调失真 (TTIMD) | 啪��分贝= 20 ×日志10{Σ (AIMF_SUM[有效值] + AIMF_DIFF[有效值])/一个基本[rms]}.TTIMD 设置中的IMF_SUM和IMF_DIFF仅包含两个输入音。 |
| 多音调互调失真 (MTIMD) | 米蒂姆德分贝= 20 ×日志10{Σ (AIMF_SUM[ 有效值] + AIMF_DIFF[有效值])/一个基本[rms]}.MTIMD 设置中的IMF_SUM和IMF_DIFF包含两个以上(通常最多四个)输入音。 |
| 电压驻波比 (VSWR) | VSWR = (1 + |ρ |) / (1 - |ρ |),其中 ρ 表示反射系数。 |
测试设置的电路板布局和硬件要求
为了对高速数据转换器进行充分的动态测试,应使用制造商预组装的测试板或遵循数据手册的电路板布局建议。本文先研究动态测试的布局要求,然后再深入研究硬件和软件的详细信息。用于快速数据转换器的评估或表征板(图1a)必须采用高速布局技术(图1b和1c)。您通常可以通过遵循以下基本规则来复制数据手册中指定的动态性能:
将所有旁路电容放置在尽可能靠近器件的位置,最好与ADC位于同一侧,使用表面贴装元件以实现最小的走线长度、电感和电容。
旁路模拟和数字电源、基准和共模输入,并联两个0.1μF陶瓷电容和一个2.2μF双极性电容接地。
具有独立接地层和电源层的多层板可产生最高水平的信号完整性。
考虑使用分离式接地层,以匹配ADC封装上模拟和数字接地的物理位置。两个接地层的阻抗必须保持在尽可能低的水平,并且为避免可能的损坏或闩锁,它们的交流和直流电压差(或两者)必须小于0.3V。这些接地应连接在单个点上,以便噪声数字接地电流不会干扰模拟接地层。这种连接的理想位置可以通过实验确定,作为沿两个接地平面之间间隙的点,产生最佳结果。这种连接可以通过1ν至5ν的低值表面贴装电阻器、铁氧体磁珠或直接短路来实现。
作为替代方案(如果接地层与下行输出缓冲器和DSP等噪声数字系统充分隔离),所有接地引脚可以共享同一接地层。
将高速数字信号走线远离敏感的模拟走线。
保持所有信号线短且无 90° 转弯。
始终将时钟输入视为模拟输入。将其路由远离实际模拟输入和其他数字信号线。
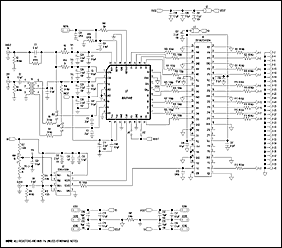
图 1a. MAX1448评估板电路原理图
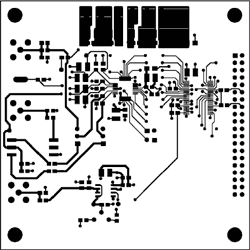
图 1b. MAX1448评估板,优化的PCB布局(元件侧)。

图 1c. MAX1448评估板,优化的PCB布局(焊接侧)。
适当的测试设置和正确的测试设备1是实现给定转换器指定性能所必需的(图 2a 和 2b)。
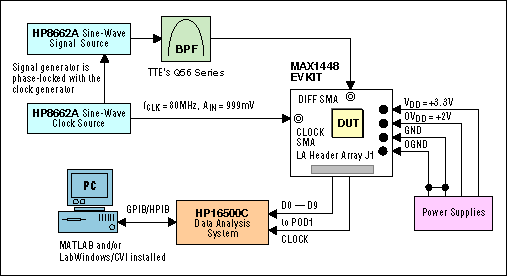
图 2a.用于测试 SNR、SINAD、THD 和 SFDR 的系统配置。
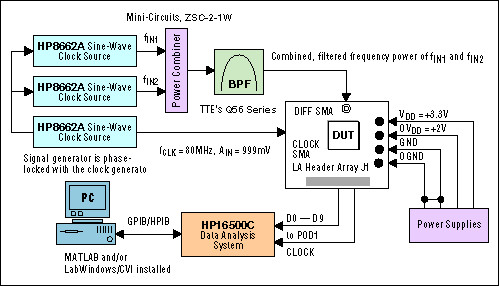
图 2b.用于测试双音 IMD 的系统配置。
以下硬件2已被证明非常有效,因此建议用于测试设置:
直流电源:慧与E3620A双电源0-25V/0-1A。为模拟节点和数字节点使用单独的电源。每个必须提供100mA的输出驱动电流。
时钟信号函数发生器:惠普HP8662A。被测器件(DUT)的时钟输入接受CMOS兼容的时钟信号。该信号应具有低抖动和快速上升和下降时间,因为高速ADC具有10级流水线,其级间转换取决于外部时钟上升沿和下降沿的可重复性。采样发生在时钟信号的下降沿,因此边沿应具有尽可能低的抖动。显著的孔径抖动限制了ADC的SNR性能,具体如下:
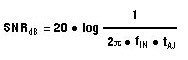
,
其中 f在表示模拟输入频率和tAJ是孔径抖动的时间。时钟抖动尤其重要 用于欠采样应用。
输入信号函数发生器:惠普HP8662A。为了正常工作,该函数发生器应锁相到时钟信号发生器。
逻辑分析仪 (LA):惠普 HP16500C。根据建议的FFT中的点数,您可以使用内存深度较小的LA(例如HP4C中提供的1663k数据记录)捕获数据。
模拟带通滤波器:TTE椭圆功能带通滤波器,Q56系列。截止频率为 7.5MHz、20MHz、40MHz 和 50MHz。
数字万用表 (DMM):设置中使用了各种福禄克、吉时利仪器和 HP 万用表(包括手持式 HP2373A 和交流供电的 HP34401A)来检查正确的参考电压、电源电压和共模电压。
评估被测设备
为了简化DUT的评估,它使用性能优化、完全组装和测试的表面贴装板进行了测试。请按照以下步骤配置设置并操作此板。在打开电源或启用函数发生器之前,应完成所有连接。
将+3.0V模拟电源连接到VAIN1和VAIN2,然后连接 其地面终端到AGND。
将 +3.0V 数字电源连接到 VDIN1 和 VDIN2,然后连接 其地面终端到DGND。
验证是否没有为跳线 JU1 安装分流器(禁用关机) 和 JU2(启用数字输出)。
将时钟函数发生器连接到时钟 SMA 连接器。
将模拟信号函数发生器的输出连接到 其中一个带通滤波器的输入。
要评估差分模拟信号,请验证是否安装了分流器 在跳线 JU1 和 JU2 的引脚 3 和 4 上。连接带通的输出 筛选到 SMA 中的差异连接器。
要评估单端模拟信号,请验证是否安装了分流器 在跳线 JU2 和 JU3 的引脚 3 和 4 上,并连接 单输入 SMA 连接器的带通滤波器。
将其中一根逻辑分析仪接口电缆(吊舱)连接到 方形针头 J1。
打开两个电源,并验证测试点的+1.20V TP4 和带电压表的 TP5。如有必要,调整电位计R34 获得+1.20V电压。
启用函数生成器。将时钟函数发生器设置为其最大输出幅度(建议的HP999A为8662mV),时钟频率为f时钟= 80兆赫。将模拟信号函数发生器设置为所需的输入音,幅度在 10μV 和 999mV 之间。请注意,输入幅度和频率必须根据带通滤波器的转折频率进行选择。用于评估高速数据转换器的带通滤波器通常具有非常窄的通带。为了获得最佳性能(当然,取决于滤波器类型和制造商),应将输入音设置为转折频率的5%以内。由于滤波器会衰减发生器的输出信号,因此请将发生器的幅度设置得略高,以达到所需的满量程输入规格。
为了正常工作,请锁相两个(三个,如果测试双音IMD)函数发生器。
将LA与来自电路板的外部时钟信号同步,并将LA设置为在时钟的上升沿锁存数据。
启用 LA 并开始收集数据。数据可以存储在软盘、LA 硬盘或通过 LA 的 HPIB 总线进行通信的数据采集 (DAQ) 板上。
现在,测试设置和硬件配置的必要步骤已经完成,系统已准备好从DUT捕获数据,是时候选择用于数据捕获和分析的软件工具了:
LabWindows/CVI™用作 LA 和 DAQ 控制器 板 之间 所需 的 数据 捕获 和 通信 链路。(本文将不讨论用于此目的的基于 C 的程序例程。
马特实验室™是一个强大的工具,可以对捕获的数据进行FFT和动态分析。
为了帮助您了解 MATLAB 程序例程如何分析和绘制高速数据转换器的动态性能,下一节将回顾一些 FFT 和功率谱基础知识。
功率谱、箱、频谱泄漏和窗口
快速傅里叶变换 (FFT) 和功率谱是测量和分析来自捕获数据记录的信号的强大工具。它们可以捕获时域信号,测量其频率成分,将结果转换为方便的单位并显示它们。然而,要执行基于FFT的测量,必须了解所涉及的问题和计算。基于FFT的信号分析的基本功能是FFT本身和功率谱。两者都对于测量稳态或瞬态信号的频率成分非常有用。FFT通常在采集信号的时间间隔内产生信号频率成分的平均值。因此,始终建议将FFT用于稳态信号分析。
双面到单面功率谱转换
信号分析中最基本和最重要的计算是使用FFT从双侧功率谱转换为单侧功率谱,调整频率分辨率并显示频谱。功率谱通常返回一个矩阵,其中包含频域中时域信号功率的双侧表示。该矩阵中的值与构成时域信号的每个频率分量的幅度平方成正比。
双侧功率谱图通常包含负频率分量和正频率分量。然而,实际的频率分析工具只关注频谱的正半部分,注意真实信号的频谱在直流周围是对称的。因此,负频率信息无关紧要。在双侧频谱中,一半能量驻留在正频率中,一半驻留在负频率中。因此,要从双侧频谱转换为单侧频谱,请丢弃矩阵的后半部分并将每个点(DC 除外)乘以 2。
箱和频率分辨率
频谱图x轴上的频率范围和分辨率(参见下面的程序代码提取)取决于采样率和数据记录的大小(采集点的数量)。功率谱中的频率点或线路数为 N/2,其中 N 是在时域中捕获的信号点数。功率谱中的第一条频率线始终代表直流。最后一条频率线可以在f处找到样本/2 - F样本频率线以 f 的偶数间隔间隔样本/N,通常称为频率箱或FFT箱(图3)。
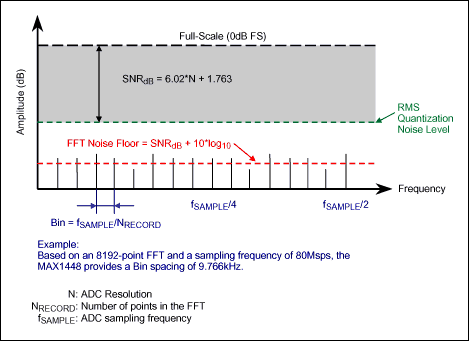
图3.FFT 图中频率/FFT 箱的表示形式。
还可以参考ADC的采样周期计算箱:
箱 = f样本/N = 1/(N ×Δt样本)
例如,采样频率为 f样本= 82.345MHz,记录长度为8,192个数据点,FFT图中每条频率线之间的距离正好是10.052kHz。(请参阅图1 中定义和测试高速ADC中的动态参数,第1部分。)
频率轴(x轴)的计算证明采样频率决定了频谱的范围或带宽。对于给定的采样频率,时域中采集的点数决定了分辨率频率。为了提高给定频率范围的分辨率,可以在相同的采样频率下增加数据记录的深度(请参阅下面的程序代码提取)。
%查找信号箱编号,DC = 箱 1 鳍=查找(Dout_dB(1:numpt/2)==最大dB);
每侧
输入频率的%跨度=max(round(numpt/200),5);
%每个谐波的近似搜索范围 侧
跨=2;
%确定功率谱
P=(abs(Dout_spect)).×(abs(Dout_spect));
%查找直流偏置功率
Pdc=sum(spectP(1:span));
%提取总信号功率
Ps=sum(spectP(fin-span:fin+span));
%矢量/矩阵,用于存储频率和功率 信号和谐波
Fh=[];
%向量/矩阵中的第一个元素表示 信号,下一个元素表示 % 二次谐波,依此类推。
Ph=[];
光谱泄漏和窗口功能
窗口函数在FFT分析中很常见,它们的正确使用在基于FFT的测量中至关重要。以下关于频谱泄漏的讨论强调需要选择合适的窗口函数,并针对给定应用对其进行适当缩放。然而,为了准确确定频谱泄漏,使用适当的信号采集技术,将双侧功率谱转换为单侧功率谱,并重新调整结果可能是不够的。为了更好地理解这个术语,应该在光谱纯正弦输入上执行N点FFT。
频谱泄漏是FFT算法中假设时间记录在所有时间中精确重复的结果,并且该时间记录中包含的所有信号都是周期性的,间隔对应于时间记录的长度。但是,时间记录中的非整数周期数(f在/f样本

N窗/ N记录) 违反此条件并导致光谱泄漏(图 4)。(请参阅第 2 部分的附录 1。只有两种情况可以保证获得整数个周期:
相对于输入音的同步采样
捕获完全适合时间的瞬态信号 记录
但是,在大多数情况下,应用程序会处理未知的静止装置3输入。这意味着不能保证对整数个周期进行采样。频谱泄漏通过将给定频率分量的能量分散到相邻的频率线或箱上来扭曲测量。选择合适的窗口功能可以最大限度地减少这种光谱泄漏的影响。
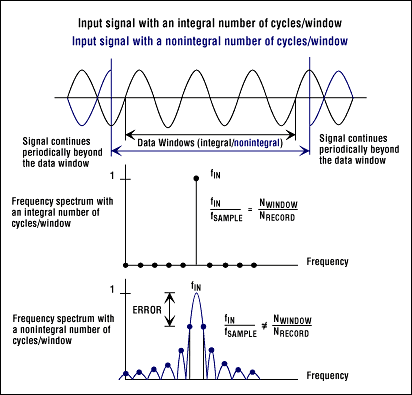
图4.窗口对光谱泄漏的影响。
为了充分了解给定的窗口函数如何影响频谱,必须仔细研究窗口的频率特性。输入数据的窗口化相当于将原始信号的频谱与窗口的频谱进行卷积。即使对于相干采样4,信号与高度均匀的矩形窗口卷积。这种卷积显示出典型的正弦函数特征谱。
窗口的实频特性是由一个主瓣和几个旁瓣组成的连续频谱。主瓣以时域中信号的每个频率分量为中心。旁瓣在主瓣两侧每隔一段时间接近零。另一方面,FFT产生离散频谱。窗口的连续周期频谱由FFT采样,就像ADC在时域中对输入信号进行采样一样。FFT的每个频率线中显示的是每个FFT频率线上连续卷积频谱的值。
如果原始信号的频率分量与频率线完全匹配,就像您获得整数个周期时的情况一样,则只能看到频谱的主瓣。旁瓣不会出现,因为主瓣两侧的窗口频谱以bin频率间隔接近零。如果时间记录不包含整数个周期,则窗口的连续频谱将从主瓣中心偏移,其频率箱对应于频率分量和FFT频率线之差的分数。这种偏移导致旁瓣出现在频谱中。因此,窗口的旁瓣特性直接影响相邻频率分量“泄漏”到相邻频率箱的程度。
窗口特性
在选择合适的窗口之前,有必要定义使用户能够比较窗口的参数和特征。这些特性包括-3dB主瓣宽度、-6dB主瓣宽度、最大旁瓣电平和旁瓣滚降率(表1)。
窗口的旁瓣的特征在于旁瓣峰值的最大旁瓣电平(定义为相对于主瓣峰值增益的最大旁瓣电平,以dB为单位)和旁瓣滚降(定义为以dB/十倍频程或dB/倍频程为单位的频率渐近衰减率)。
| 窗口类型 | -3dB 主瓣宽度 | -6dB 主瓣宽度 | 最大旁瓣电平 | 旁瓣滚降率 |
| 无窗(制服) | 0.89 垃圾箱 | 1.21 垃圾箱 | -13分贝 | 20分贝/十倍频程,6分贝/倍频程 |
| 汉宁 | 1.44 垃圾箱 | 2.00 垃圾箱 | -32分贝 | 60分贝/十倍频程,18分贝/倍频程 |
| 汉明 | 1.30 垃圾箱 | 1.81 垃圾箱 | -43分贝 | 20分贝/十倍频程,6分贝/倍频程 |
| 平顶 | 2.94 垃圾箱 | 3.56 垃圾箱 | -44分贝 | 20分贝/十倍频程,6分贝/倍频程 |
选择正确的窗口
不同的窗口适合不同的应用。要选择正确的频谱窗口,必须猜测信号频率成分。如果信号包含远离目标频率的强干扰频率分量,则应选择旁瓣具有高滚降速率的窗口。如果强干扰信号接近目标频率,则具有低最大旁瓣电平的窗口更合适。
如果感兴趣的频段包含两个或多个彼此靠近的信号,则频谱分辨率变得很重要。在这种情况下,具有窄主瓣的窗口更好。对于单个频率分量,其重点是幅度精度而不是其在频率箱中的精确位置,建议使用具有宽主瓣的窗口。最后,建议对平坦或宽带频谱使用相干采样(而不是窗口)(请参阅下面的程序代码提取)。
%如果未使用窗口功能,则必须选择唯一的输入音,并且与采样频率有关。为了实现这个素数,引入了%输入音,由f确定在= f样本×(质数/数据记录大小)。
%为了放宽这一要求,可以%引入诸如HANNING和HAMING(见下文)之类的窗口函数,但是在不使用窗口函数的情况下,生成的FFT频谱中的基本面似乎“更清晰” %。
杜特=杜特;
%Doutw=Dout.×hanning(numpt);
%Doutw=Dout.×hamming(numpt);
%执行快速傅里叶 变换
Dout_spect=fft(Doutw);
%重新计算为dB
Dout_dB=20×log10(abs(Dout_spect));
%以频率显示结果 具有FFT绘图
的域;
maxdB=max(Dout_dB(1:numpt/2));
汉宁窗口功能具有良好的频率分辨率并减少频谱泄漏,在大多数应用中都能产生令人满意的结果。平顶窗口具有良好的振幅精度,但其宽主瓣的频率分辨率较差,频谱泄漏更多。平顶窗口的最大旁瓣电平低于汉宁窗口,但汉宁窗口的滚降速率更快。
仅由瞬态信号组成的应用应该根本没有频谱窗口,因为它们往往会衰减样本模块开头的重要信息。对于瞬态信号,应选择非光谱窗口,例如力或指数窗口。
选择合适的窗口并不容易,但如果信号内容未知,可以从汉宁特性开始。比较多个窗口函数的性能以找到最适合给定应用程序的函数也是一个好主意。
| 窗口类型 | 信号内容 | 窗口特性 |
| 无窗(制服) | 宽带随机、紧密间隔的正弦波信号 | 主瓣窄,滚降速率慢,频率分辨率差 |
| 汉宁 | 窄带随机信号,内容性质未知,正弦波或正弦波信号的组合 | 最大旁瓣电平高,频率分辨率高,泄漏减少,滚降速度更快 |
| 汉明 | 紧密间隔的正弦波信号 | 光谱分辨率好,主瓣窄 |
| 平顶 | 需要振幅精度的正弦波 | 振幅精度好,主瓣宽,频率分辨率差,频谱泄漏多 |
动态范围规格 SNR、SINAD、THD 和 SFDR
根据您从本文前面部分获得的知识,以下程序代码提取应该很容易理解。基于FFT、功率谱以及对频谱泄漏和窗口函数的关注,使用MATLAB计算出SNR、SINAD、THD和SFDR规格如下:
信噪比 = 10×log10(Ps/Pn) SINAD = 10×log10(Ps/(Pn+Pd)) THD = 10×log10(Pd/Ph(1)) SFDR = 10×log10(Ph(1)/max(Ph(2:10))
),
其中Ps是信号功率,Pn是噪声功率,Pd是由2次至5次谐波引起的失真功率,Ph(1)是基波谐波功率,Ph(2:10)是2次至9次谐波的谐波功率(有关功率谱电平,请参见以下程序代码提取)。
%Find harmonic frequencies and power components in the FFT spectrum
for har_num=1:10
%Input tones greater than fSAMPLE are aliased back into the spectrum
tone=rem((har_num×(fin-1)+1)/numpt,1);
if tone>0.5
%Input tones greater than 0.5×fSAMPLE (after aliasing) are reflected
tone=1-tone;
end
Fh=[Fh tone];
%For this procedure to work, ensure the folded back high order harmonics do not overlap
%with DC or signal or lower order harmonics
har_peak=max(spectP(round(tone×numpt)-spanh:round(tone×numpt)+spanh));
har_bin=find(spectP(round(tone×numpt)-spanh:round(tone×numpt)+spanh)==har_peak);
har_bin=har_bin+round(tone×numpt)-spanh-1;
Ph=[Ph sum(spectP(har_bin-1:har_bin+1))];
end
%Determine the total distortion power
Pd=sum(Ph(2:5));
%Determine the noise power
Pn=sum(spectP(1:numpt/2))-Pdc-Ps-Pd;
format;
A=(max(code)-min(code))/2^numbit
AdB=20×log10(A)
SINAD=10×log10(Ps/(Pn+Pd))
SNR=10×log10(Ps/Pn)
disp('THD is calculated from 2nd through 5th order harmonics');
THD=10×log10(Pd/Ph(1))
SFDR=10×log10(Ph(1)/max(Ph(2:10)))
disp('Signal & Harmonic Power Components:');
HD=10×log10(Ph(1:10)/Ph(1))
基于MATLAB源代码(见下文),MAX1448不仅针对其数据资料规格进行了测试,还针对许多其他过采样和欠采样输入频率进行了测试。它在所有条件下都实现了出色的动态性能。
%示例程序例程,用于生成FFT图,并根据HP16500C逻辑分析仪
%System获取的数据记录确定%a高速数据转换器的
动态性能。数据通过 HPIB 接口提取并读入以下 MATLAB
%程序例程。可以从 LA
% 的控制器接口中提取相同的数据,然后简单地复制到软盘上 — 这是一种相当耗时的方法,但有可能。
%启动MAX1448动态性能测试程序
<disp('HP16500C State Card');
filename=input('Type a:filename or Press RETURN for HPIB Data Transfer: ');
if isempty(filename)
filename = 'listing';
end
fid=fopen(filename,'r');
numpt=input('Data Record Size (Number of Points)? ');
fclk=input('Sampling Frequency (MHz)? ');
%MAX1448 - 10-bit data converter
numbit=10;
%Discard first 13 lines from the data file, which do not contain data
for i=1:13,
fgetl(fid);
end
[v1,count]=fscanf(fid,'%f',[2,numpt]);
fclose(fid);
v1=v1';
code=v1(:,2);
%Display a warning, when the input generates a code greater than full-scale
if (max(code)==2^numbit-1) | (min(code)==0)
disp('Warning: ADC may be clipping!!!');
end
%Plot results in the time domain
figure;
plot([1:numpt],code);
title('TIME DOMAIN')
xlabel('SAMPLES');
ylabel('DIGITAL OUTPUT CODE');
%重新居中数字正弦波
Dout=code-(2^numbit-1)/2;
%如果未使用窗口函数,则 输入音必须选择唯一,并且与采样频率有关
。为了实现这个质数,引入了
%输入音由下式决定 f在= f样本*(质数/数据记录大小)。
%为了放宽这一要求,可以
%引入诸如HANNING和HAMING(见下文)之类的窗口函数,但是在不使用窗口函数的情况下,生成的FFT频谱中的基本面似乎“更清晰”
%。
Doutw=Dout;
%Doutw=Dout.*hanning(numpt);
%Doutw=Dout.*hamming(numpt);
%执行快速傅里叶变换
Dout_spect=fft(Doutw);
%重新计算为dB
Dout_dB=20*log10(abs(Dout_spect));
%以频率显示结果 具有FFT绘图
的域;
maxdB=max(Dout_dB(1:numpt/2));
%对于 TTIMD,请使用以下简短 常规,归一化为 -6.5dB 满量程。
%plot([0:numpt/2-1].*fclk/numpt,Dout_dB(1:numpt/2)-maxdB-6.5);
plot([0:numpt/2-1].*fclk/numpt,Dout_dB(1:numpt/2)-maxdB);
grid on;
title('FFT PLOT');
xlabel('ANALOG INPUT FREQUENCY (MHz)');
ylabel('AMPLITUDE (dB)');
a1=axis; axis([a1(1) a1(2) -120 a1(4)]);
%计算信噪比、正弦、THD 和 SFDR 值
%查找信号箱编号, DC = bin 1 fin=find(Dout_dB(1
:numpt/2)==maxdB);
每侧
输入频率的%跨度=max(round(numpt/200),5);
%每个谐波的近似搜索范围 侧
跨=2;
%确定功率谱
P=(abs(Dout_spect)).*(abs(Dout_spect));
%查找直流偏置功率
Pdc=sum(spectP(1:span));
%提取总信号功率
Ps=sum(spectP(fin-span:fin+span));
%向量/矩阵来存储两者 信号和谐波
的频率和功率 Fh=[];
%的 1圣向量/矩阵中的元素 表示信号,下一个元素表示
%2德·谐波等
Ph=[];
%查找谐波频率和功率 FFT 频谱中的分量
为 har_num=1:10
%输入音调大于f样本混叠回频谱
tone=rem((har_num*(fin-1)+1)/numpt,1);
中频音调>0.5
%输入音调大于 0.5*f样本(混叠后)被反射
音调=1音;
结束
Fh=[Fh 音调];
%要使此过程正常工作,请确保折叠 回高次谐波不与 直流或信号或低次谐波
重叠%har_peak=max(spectP(round(tone*numpt)-spanh:round(tone*numpt)+spanh));
har_bin=find(spectP(round(tone*numpt)-spanh:round(tone*numpt)+spanh)==har_peak);
har_bin=har_bin+圆形(音调*音调)-spanh-1;
Ph=[Ph sum(spectP(har_bin-1:har_bin+1))];
结束
%确定总失真功率
Pd=sum(Ph(2:5));
%确定噪声功率
Pn=sum(spectP(1:numpt/2))-Pdc-Ps-Pd;
格式;
A=(max(code)-min(code))/2^numbit
AdB=20*log10(A) SINAD=10*log10(Ps/(Pn+Pd)) SNR=10*log10(Ps/Pn)
disp('THD is compute 从二阶到五阶谐波');
THD=2*log5(Pd/Ph(10)) SFDR=10*log1(Ph(10)/max(Ph(10:1)))
disp('Signal & Harmonic 电源组件:');
HD=2*log10(Ph(10:10)/Ph(1))
%区分所有谐波位置 在FFT情节
hold on;
plot(Fh(2)*fclk,0,'mo',Fh(3)*fclk,0,'cx',Fh(4)*fclk,0,'r+',Fh(5)*fclk,0,'g*',... Fh(6)*fclk,0,'bs',Fh(7)*fclk,0,'bd',Fh(8)*fclk,0,'kv',Fh(9)*fclk,0,'y^');
legend('1st','2nd','3rd','4th','5th','6th','7th','8th','9th');
hold off;
动态范围规格,TTIMD
双音IMD可能是一个棘手的测量,因为所需的附加设备(组合两个输入频率的功率组合器)可能会产生不需要的互调产物,从而伪造ADC的互调失真。您必须遵守以下条件来优化IMD性能,尽管它们使选择合适的输入频率成为一项繁琐的任务。 首先,输入音必须落入输入滤波器的通带。如果这些音调靠近(兆赫兹带宽为几十或几百千赫兹),则还必须选择适当的窗口函数。然而,将它们放在太近的位置可能会允许功率组合器通过贡献不需要的二阶和三阶IMD产品(取决于输入音在通带内的位置)来伪造整体IMD读数。输入音调的间距太远可能需要频率分辨率较低的其他窗口类型。 该设置还需要至少三个锁相信号发生器。这种要求很少给测试实验室带来问题,但发生器具有不同的匹配频率和幅度的能力。补偿此类不匹配以实现(例如)-2.3dB FS双音包络和-0.5dB FS的信号幅度将增加您的工作量和测试时间(请参阅以下程序代码提取)。
%对于 TTIMD,请使用以下短例程,归一化为 -6.5dB 满量程。
%plot([0:numpt/2-1].×fclk/numpt,Dout_dB(1:numpt/2)-maxdB-6.5);
plot([0:numpt/2-1].×fclk/numpt,Dout_dB(1:numpt/2)-maxdB);
grid on;
title('FFT PLOT');
xlabel('ANALOG INPUT FREQUENCY (MHz)');
ylabel('AMPLITUDE (dB)');
a1=axis; axis([a1(1) a1(2) -120 a1(4)]);
结论
除上述几点外,工程师还面临着许多其他问题,他们试图通过捕获并分析高速ADC的信号来确定其动态范围。不幸的是,在光谱测量过程中很容易出错。但是,通过了解基于FFT的测量和相关计算,频谱泄漏的影响以及如何防止它,以及必要的布局技术和设备,可以大大减轻数据采集和分析的任务。
-
高速ADC的特征测试和生产测试方法2023-11-28 502
-
高速ADC的特征测试和生产测试方法评估笔记2023-11-27 359
-
高速ADC/DAC的测试方法分享2023-11-07 7987
-
定义和测试高速ADC中的动态参数2023-02-25 4252
-
关于高速ADC测试和评估应用2022-07-04 1795
-
blog高速ADC、DAC测试原理及测试方法2021-09-17 1232
-
高速ADC测试和评估方法2021-09-16 1204
-
怎么测试高速ADC的性能?2021-04-14 2091
-
AN-835: 高速ADC测试和评估2021-03-21 842
-
高速 ADC/DAC 测试原理及测试方法2018-04-03 10471
-
adc转换器性能的动态测试2017-08-29 859
-
高速ADC测试和评估2015-12-24 875
-
AN-835高速ADC测试和评估2013-08-21 1289
-
高速模数转换器动态参数的定义和测试2010-12-21 2107
全部0条评论

快来发表一下你的评论吧 !

