了解积分非线性误差

要了解积分非线性误差的影响，最直接的方法是分析简单的正弦波，并将众所周知的三角恒等式应用于包含INL误差的非理想模数输出传递函数。

对于理想的系统，具有振幅A和频率fo的单音正弦波，

X(t) = Asin(2π fot)

使用周期为T的ADC采样会产生离散信号：

X[n]=Asin(2π fonT),

其中 X[n] 是从每 T 秒对 X（t） 进行均匀采样获得的离散时间信号。倒数 1/T = F 称为采样率或采样频率。

一类特别重要的系统由线性和时间不变的系统组成，或“LTI”。这两个属性相结合，为此类系统提供了特别方便的表示形式。最重要的是，LTI 系统 X[n] 的输入和输出 Y[n] 之间的关系可以通过卷积和给出。卷积是分析和描述LTI系统的基础。在这个例子中，我们将只分析系统的线性度。

线性系统是满足叠加原理的系统。简单地说，叠加原理要求系统对信号加权和的响应等于系统对每个单独输入信号的响应（输出）的相应加权和。叠加特性大大简化了线性系统的分析。由于分解属性，您可以分别计算输出的不同组件。

将理想的ADC传输曲线与具有INL误差的传输曲线进行比较，很容易演示具有INL误差的系统如何产生非线性输出。当输出 Y3[n] = X1[n] + X2[n] 时，输出 Y3[n] 不等于输出 Y1[n] +Y2[n] 的总和。更准确地说，F（X1 + X2）≠F（X1）+ F（X2）。因此，非线性误差会产生额外的、不需要的内部生成的正弦波，从而增加设计成本和滤波器复杂性。（电气工程师将内部生成的正弦波的这种影响视为互调失真。

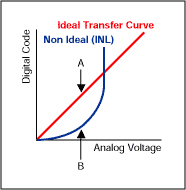
图1.箭头 A 的尖端和箭头 B 的尖端之间的距离是 INL 误差的度量。

在上图中，理想的传递函数绘制为直线。在本例中，包括INL误差的非理想传递曲线绘制为二阶函数Y[n] = k[X[n]]^2。实际上，非理想传递函数还可以包含二阶、三阶、四阶等，分量 Y[n] = kX1[n] + k2X[n]^2 + k3X[n]^3 + k4X[n]^4 + ...

对于以下分析，仅考虑二阶分量。

X1[n] = sin（2π × fo × nT） fo = 1Hz（为清楚起见，将fo分开），振幅A=1，无相位

Y1[n] = kX1[n]X1[n] 为简单起见，在本例中设置常量 k = 1

Y1[n] = sin（2π × 1 × nT）sin（2π × 1 × nT）

注意：从三角恒等式中回想一下，Sin（A）Sin（B） = Cos（A-B）/2 - Cos（A+B）/2

Y1[n] = cos（2π × 1 × nT - 2π × 1 × nT）/2 - cos（2π × 1 × nT + 2π × 1 × nT）/2

Y1[n] = cos（0）/2 - cos（4π × 1 × nT）/2

Y1[n] = 1/2 - cos（2π × 2 × nT）/2 （fo = 2Hz 且峰值振幅为 -0.5 的余弦波）

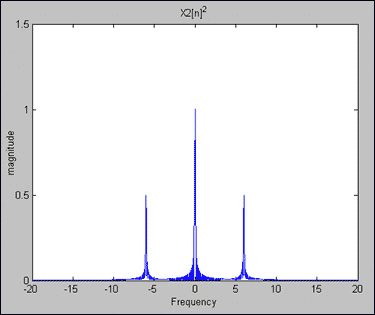
图2.Y2[n] = X2[n]2= 1/2 - cos（2π × 6 × nT）/2.

X2[n] = sin（2π × fo × nT），fo = 3Hz，振幅 A=1

Y2[n] = sin（2π × 3 × nT）sin（2π × 3 × nT）

Y2[n] = cos（2π × 3 × nT - 2π × 3 × nT）/2 - cos（2π × 3 × nT + 2π × 3 × nT）/2

Y2[n] = cos（0）/2 - cos（4π × 3 × nT）/2

Y2[n] = 1/2 - cos（2π × 6 × nT）/2 （fo = 6Hz 且峰值振幅为 -0.5 的余弦波）

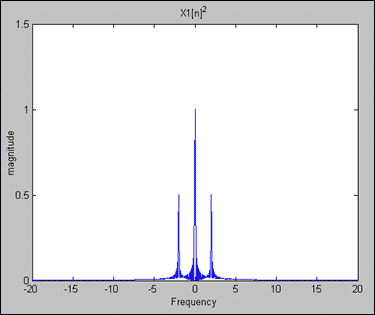
图3.Y1[n] = X1[n]2= 1/2 - cos（2π × 2 × nT）/2.

我们现在可以应用 X3[n] = X1[n] + X2[n] ，其中 Y3[n] = [X[3]]^2

Y3[n] = [ X1[n] + X2[n] ]^2

Y3[n] = X1[n]X1[n] + 2 X1[n]X2[n] + X2[n]X2[n]

如前所述：

X1[n]X1[n] 导致恒定值为 1/2，余弦波为 2Hz，振幅为 -0.5

X2[n]X2[n] 导致恒定值为 1/2，余弦波为 6Hz，振幅为 -0.5

 

For 2X1[n]X2[n] = 2sin(2π × 1 × nT)sin(2π × 3 × nT)
                = cos(2π × 1 × nT - 2π × 3 × nT) - cos(2π × 1 × nT + 2π × 3 × nT)
                = cos(-4π × nT) - cos(8π × nT)
                = cos(-2π × 2 × nT) - cos(2π × 4 × nT)
                = cos(2π × 2 × nT) - cos(2π × 4 × nT)    (cosine waves of 2Hz and 4Hz)

因此

 

For Y3[n]   = X1[n]^2 + X2[n]^2
            = Y1[n] + Y2[n]
            = 1 - cos(2π × 2 × nT)/2  - cos(2π × 6 × nT)/2

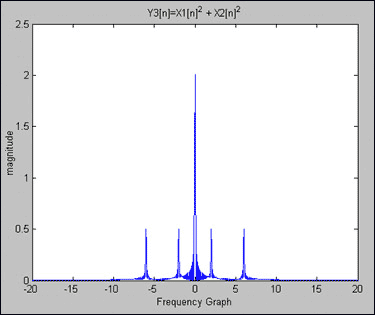
图4.Y3[n] = X1[n]^2 = 1 - cos（2π × 2 × nT）/2 - cos（2π × 6 × nT）/2.

然而

 

For Y3[n]   = ( X1[n] + X2[n] )^2
            = 1 - cos(2π × 2 × nT)/2 - cos(2π × 6 × nT)/2 + cos(2π × 2 × nT) - cos(2π × 4 × nT)

 

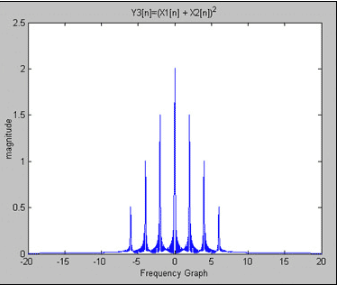
图5.Y3[n] = X1[n] + X2[n]）^2 = 1 - cos（2π × 2 × nT）/2 - cos（2π × 6 × nT）/2 + cos（2π × 4 × nT）。

由于积分非线性误差，我们增加了两个额外的2Hz和4Hz余弦波。不满足叠加原理，因此该系统是非线性的，不是线性时不变系统。如上所述，需要应用滤波来抑制额外的无用频率（或旁瓣），从而增加了设计的复杂性和成本。