

使用二极管和三极管构成的逻辑门电路
模拟技术
描述
今天我们讲讲简单的逻辑门电路。我们知道,逻辑门电路是指能够实现各种基本逻辑关系的电路。“与”、“或”、“非”这三种基本的,当然还有“与非”、“异或”、“同或”啦等等。
今天就来看看用二极管、三极管构成的简单逻辑“与”、“或”、“非”门电路。
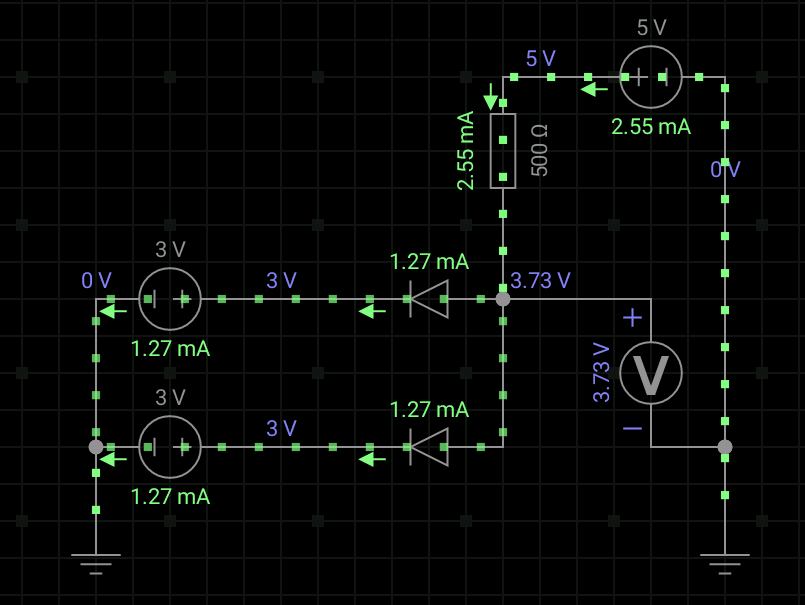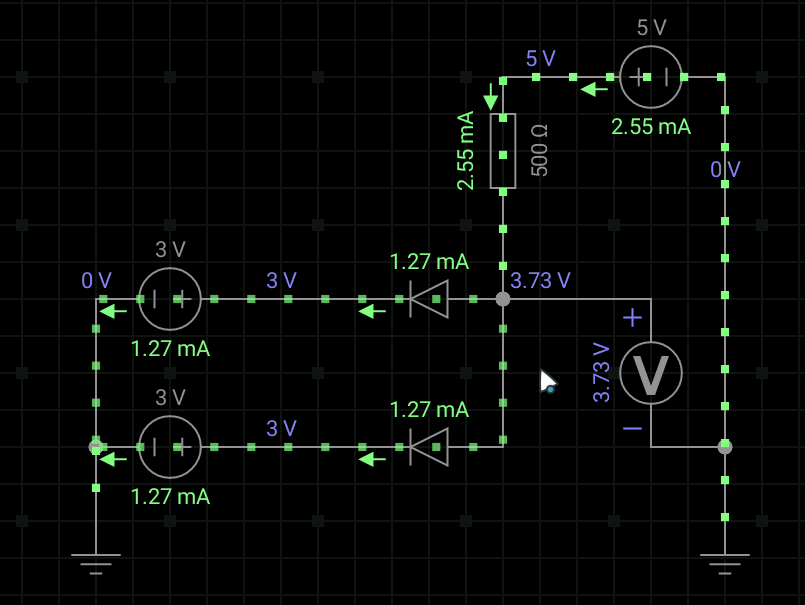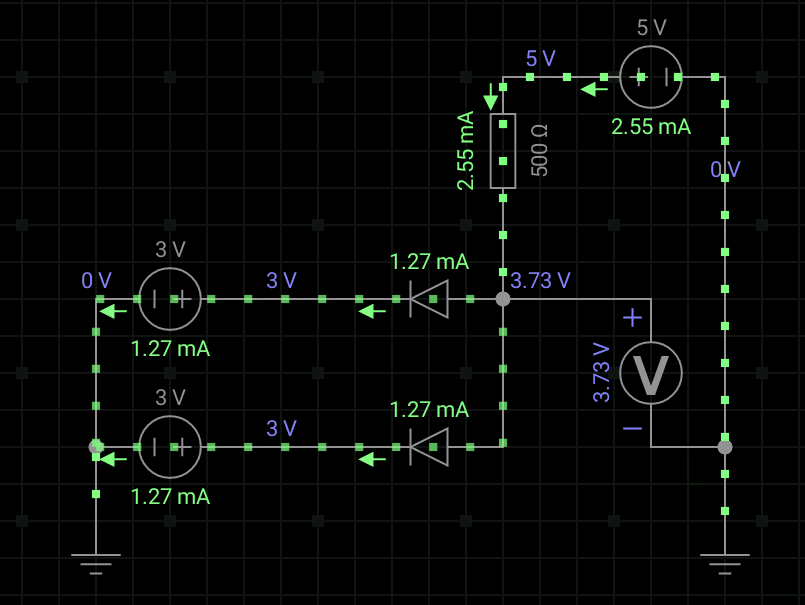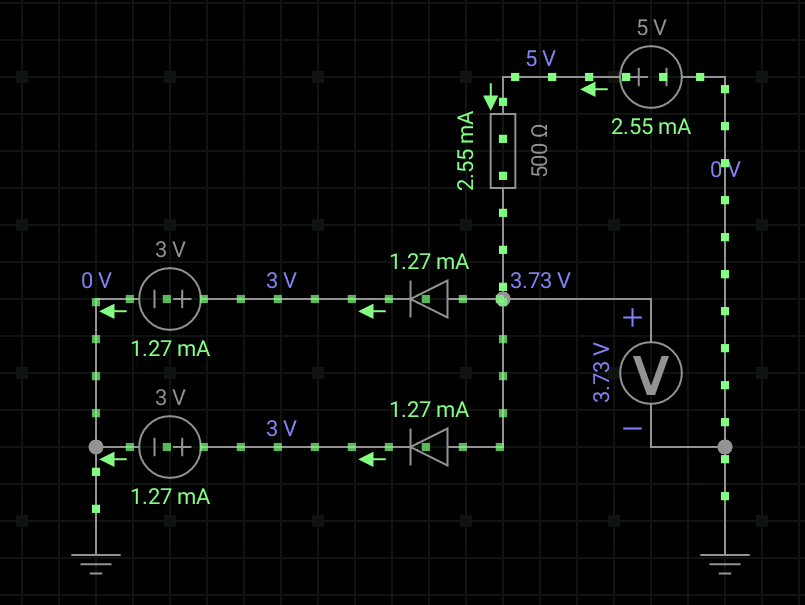
1、二极管与门
我们先来看看它的电路图:
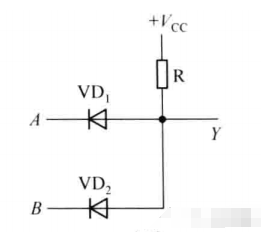
上一期,我们分析过二极管的动态开关特性,同样的,这里的电路结构还是比较简单的。我们假设Vcc=5V,A、B输入端输入的高低电平分别为UIH=3V和UIL=0V,二极管VD1和VD2的正向导通压降为0.7V,Y为输出端。
分析:
①当我们在A和B输入端加的电压均为0V时,二极管VD1和VD2也都导通,则输出端Y的电压就是二极管两端为0.7V;
②当A和B端其中一个为低电平0V,一个为高电平3V。我们知道,二极管,谁阳极和阴极电压差大,谁就先导通。我们假设UA=0V,UB=3V,那么VD1就先导通,这样,Y点的电势就是0.7V,那么VD2因此截止。综上所述,输出端Y的电压也是0.7V;
③当A和B加的电压都是3V,那么,两个二极管VD1和VD2都处于导通的状态,互不影响。于是输出端Y的电压就是3.7V。
如果,我们规定3V以上是“高电平”,用逻辑“1”来表示;0.7V以下是“低电平”,用逻辑“0”来表示。可以得到Y、A、B三者之间存在“与的关系”。Y=AB。
我们看看逻辑电平表和真值表,下面也是我仿真的动态图。
|
A/V |
B/V |
Y/V |
|
0 |
0 |
0.7 |
| 0 |
3 |
0.7 |
|
3 |
0 |
0.7 |
|
3 |
3 |
3.7 |
|
A |
B |
Y |
|
0 |
0 | 0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 | 1 |
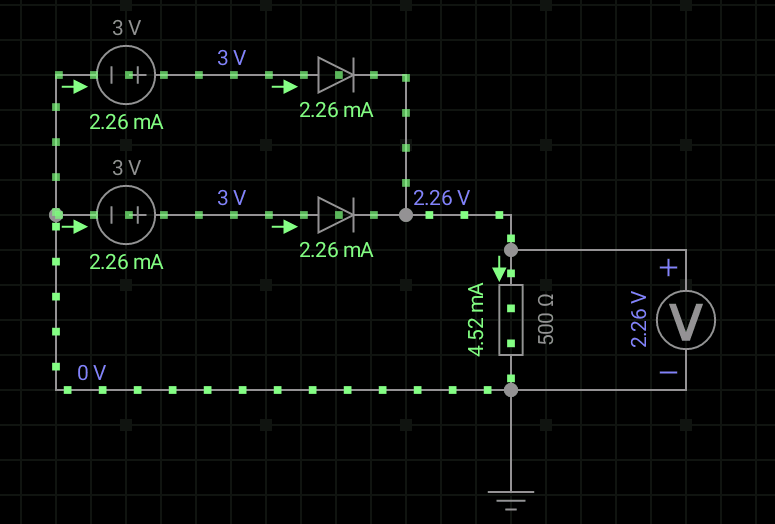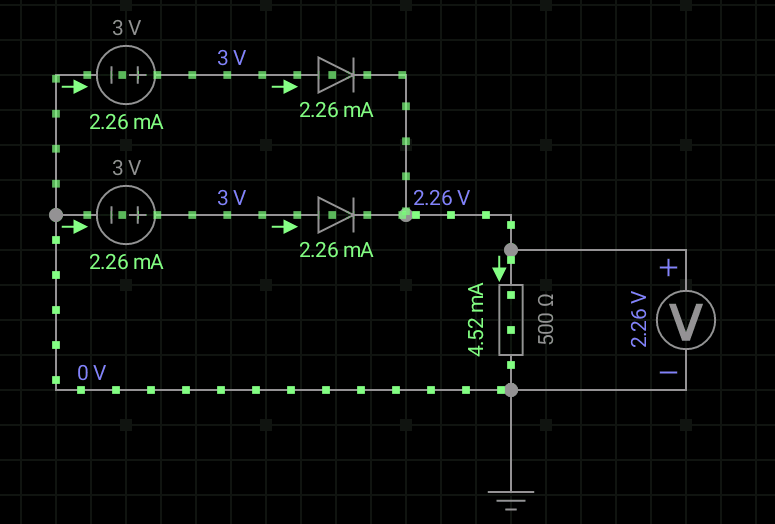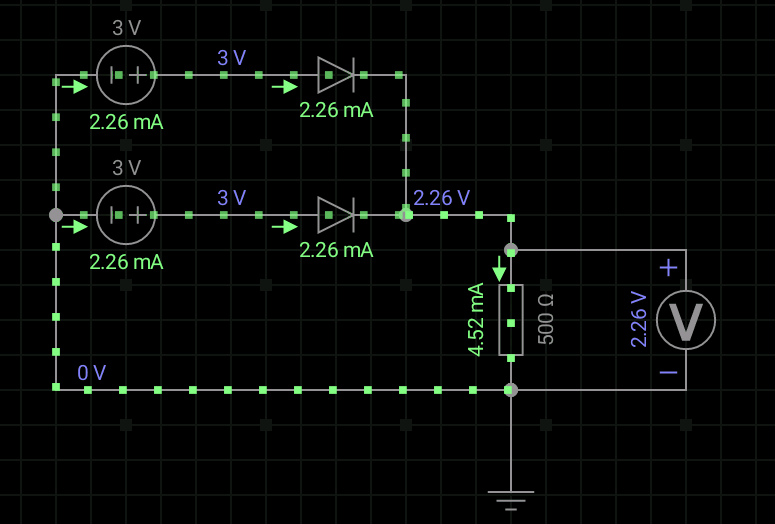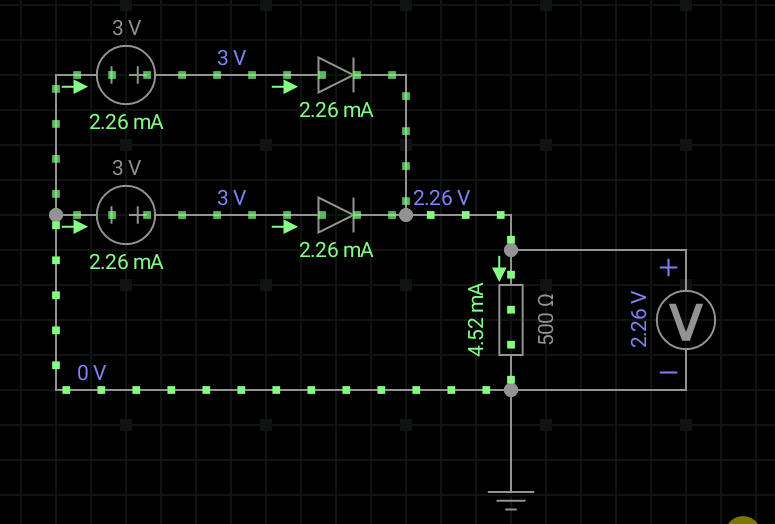
2、二极管或门
我们首先来看看电路图:
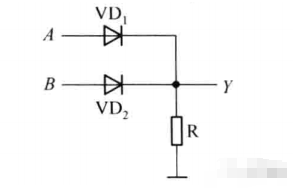
这里的参数和上面的一样,我们就直接来分析吧。
分析:
①当A和B输入的均为0V时,电路没电源,根本就不导通,输出端Y电压为0;
②当A和B输入端其中一个为3V时,假设UA=3V,UB=0V,VD1导通,VD2截止,此时输出端Y的电压为3-0.7=2.3V;
③当A和B输入的电压都是3V时,和上一个的电路一样,VD1和VD2均导通,所以输出端Y的电压为3-0.7=2.3V。
这里,我们仍然认为2.3V算是高电平。得到逻辑关系Y=A+B。我们看看逻辑电平表和真值表。
|
A/V |
B/V |
Y/V |
|
0 |
0 |
0 |
|
0 |
3 |
2.3 |
|
3 |
0 |
2.3 |
|
3 |
3 |
2.3 |
|
A |
B |
Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
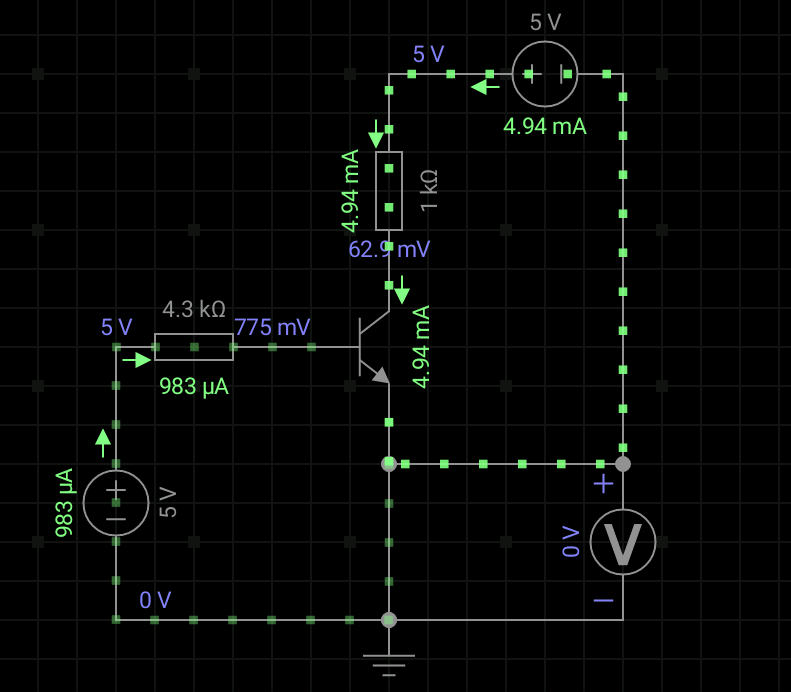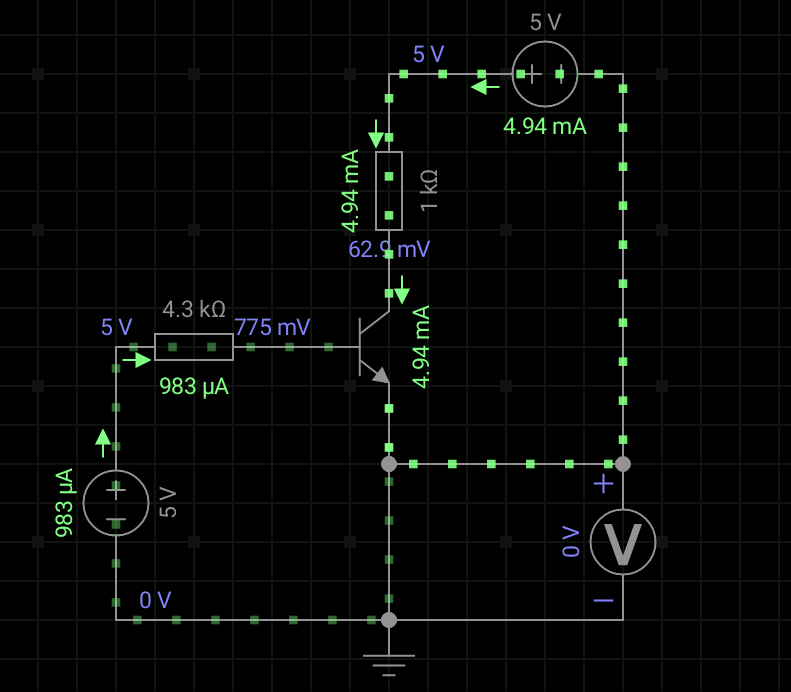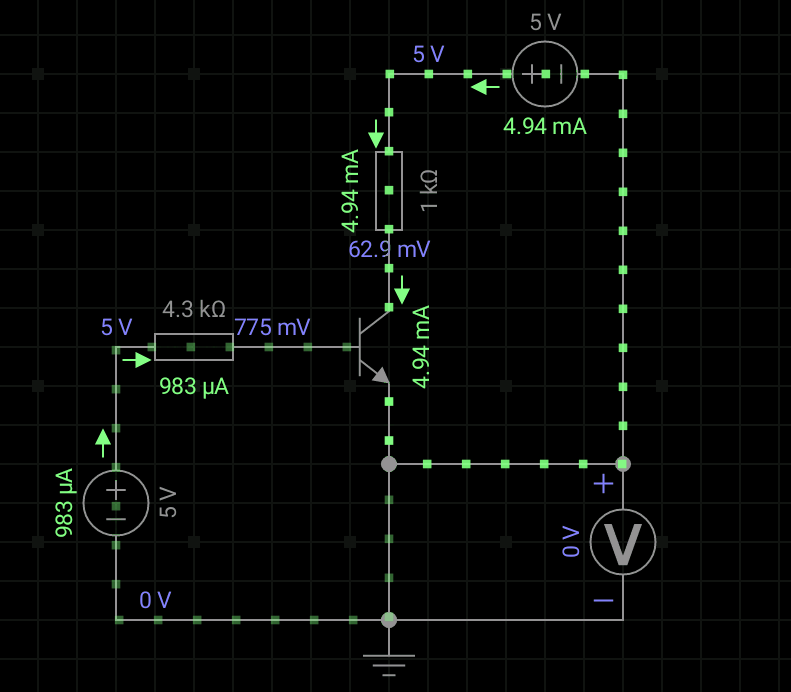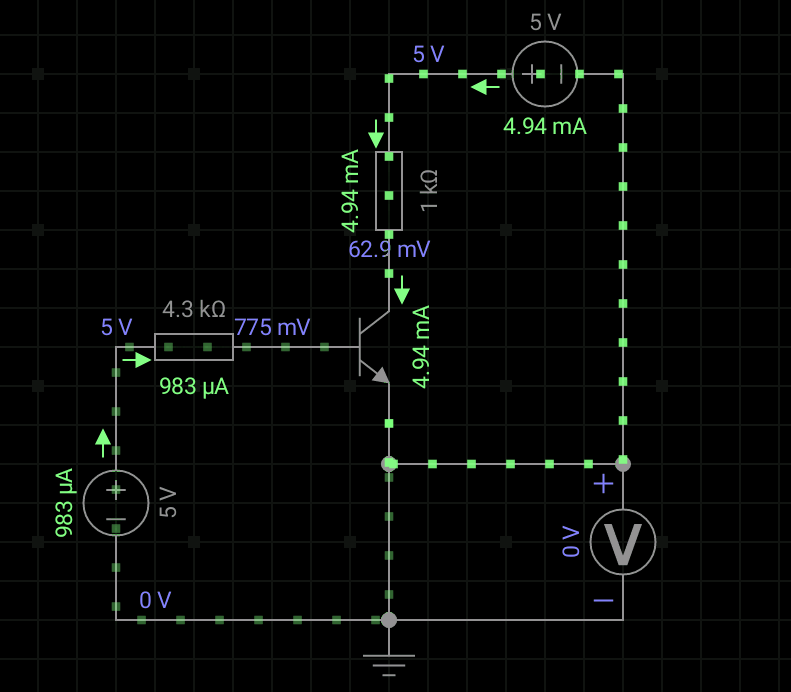
3、三极管非门
我们首先来看看电路图:
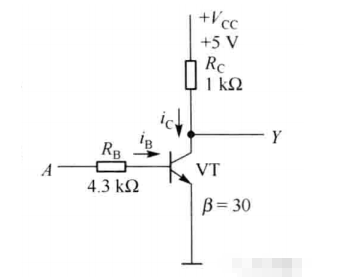
有了上一期,我们分析三极管的开关特性,这里我们理解由三极管构成的非门就容易不少。
我们假设输入端电压高电平为5V,低电平就是0V,那么UA=0V时,三极管就是截止的,所以Vcc-Rc-Y构成回路,Y端输出电压就是高电平5V。当我们在A端输入电压5V时,假设参数很理想,使得三极管处于饱和状态,此时输出端Y的电压就是UCES=0.3V,低电平。
今天的内容就到这里,我们下期再见。
-
二极管和三极管的区别2023-09-09 13147
-
三极管当二极管的使用方式2022-11-11 16224
-
谈谈二极管与门电路的原理是什么?2021-07-11 3347
-
如何使用三极管二极管和电阻实现逻辑门电路2020-12-09 1784
-
二极管和三极管的区别联系2020-03-09 52378
-
【实用】逻辑门器件,直接用二极管、三极管搭建!2019-07-09 12702
-
逻辑门器件,直接用二极管、三极管搭建!2019-07-08 3750
-
电阻、二极管、三极管搭出的各种逻辑电路2018-10-11 6616
-
二极管与门和三极管非门电路原理2018-03-01 27404
-
二极管与、或门,三极管非门电路原理2018-01-14 144546
-
经验分享:三极管和二极管组成的逻辑门电路2015-02-11 28313
-
光敏三极管工作原理/光敏二极管原理2009-12-01 4688
-
二极管和三极管的工作原理是什么2009-11-05 14136
-
半导体二极管和三极管2008-12-04 1433
全部0条评论

快来发表一下你的评论吧 !

