通过减法和非减法抖动减少量化失真

了解抖动如何抑制谐波和非谐波杂散以及两种不同类型的抖动系统：减法和非减法拓扑。

量化小幅度信号 可以在 量化误差 和输入，导致重要的谐波分量。高频 谐波 可以混叠回奈奎斯特间隔的频率，该频率可能是也可能不是输入的谐波。

在本文中，我们将看到抖动可以抑制谐波和非谐波杂散。我们还将介绍两种不同类型的抖动系统，即减法和非减法拓扑，并了解每种类型的重要功能。

量化小信号时的高频谐波

之前，我们讨论过即使是理想的 模数转换器 （ADC） 在数字化低振幅信号时产生谐波分量。例如，通过量化幅度为 0.75 LSB （最低有效位），我们在图1的时域中得到以下波形。

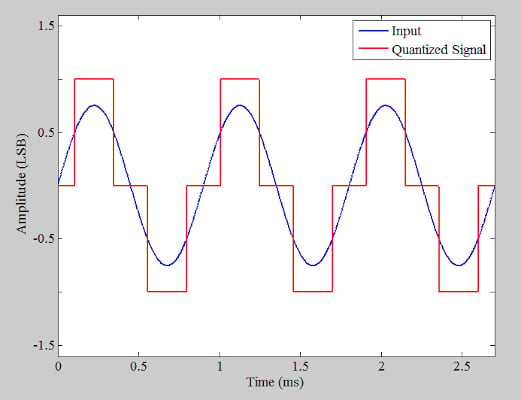
图1. 显示输入和量化信号的图。 

在4 MHz处对量化信号（上面的红色曲线）进行采样，并取其FFT（快速傅里叶变换），我们得到下面的频谱（图2仅显示DC至200 kHz范围）。

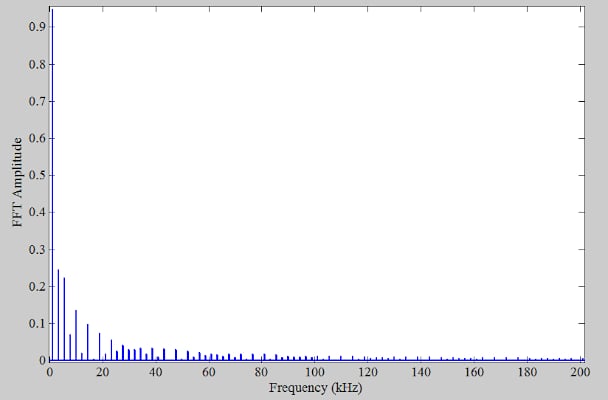
图2. f的输出频谱s = 4 兆赫。

如本文第一部分所述，输出频谱中的谐波是量化操作的伪影。通过目视检查，我们观察到这些谐波在高达180 kHz的频率下很容易辨别。为了产生上述曲线，我们故意使用远高于 奈奎斯特采样定理.这种高采样频率使我们能够获得信号的真实频谱，而不受有限采样频率的影响（就好像信号是未采样的模拟信号一样）。

量化低振幅信号引起的混叠效应

如果我们使用较低的采样率（例如40 kHz）来获取输出样本会怎样？根据奈奎斯特采样准则，40 kHz足以成功采样和重建1.11 kHz正弦波。然而，类似方波的信号具有高达40 kHz和超过40 kHz的显着谐波分量。例如，33次和35次谐波（36.63 kHz和38.85 kHz）略低于我们的新采样频率fs = 40 kHz（图 3）。

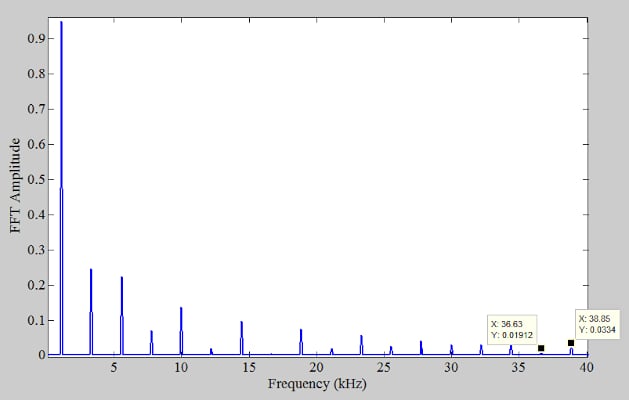
图3. f的放大光谱s = 4 兆赫。

考虑到上述频谱，40 kHz的采样频率实际上并不满足奈奎斯特的采样条件。因此，通过以40 kHz采样，所有高于20 kHz的谐波都将混叠回奈奎斯特间隔，其频率可能是也可能不是输入的谐波。图4显示了采样频率为40 kHz时的输出频谱。

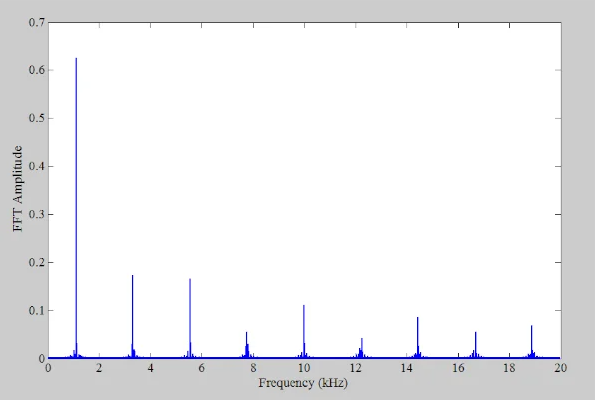
图4. f的输出频谱s = 40 kHz。

上述频谱中有谐波和非谐波分量。从图3可以看出，当使用40 kHz采样频率时，我们预计36.63 kHz和38.85 kHz的分量将分别混叠回3.37 kHz和1.15 kHz。这些混叠分量如图5所示，它提供了围绕目标频率的输出频谱的放大版本。

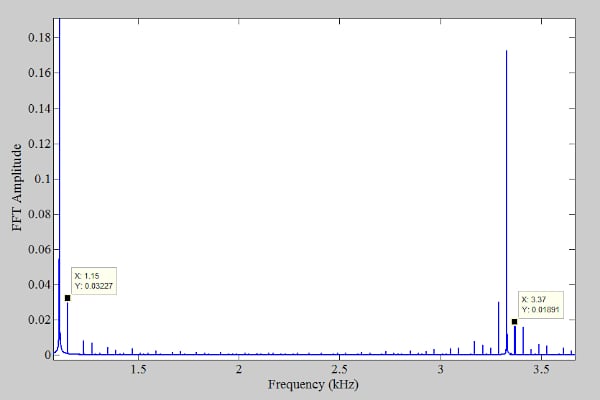
图5. 围绕感兴趣频率的输出频谱的放大版本。 

在信号中添加抖动噪声可以破坏量化误差和输入之间的相关性，从而消除量化失真。因此，当使用40 kHz采样频率和抖动时，我们预计谐波和非谐波分量将消失。为了验证这一点，我们添加了 噪声 在量化之前对输入进行三角形分布，然后以 40 kHz 进行采样。三角形抖动 PDF（概率密度函数）的宽度取为 2 LSB。在这种情况下，获得以下输出频谱（图6）。

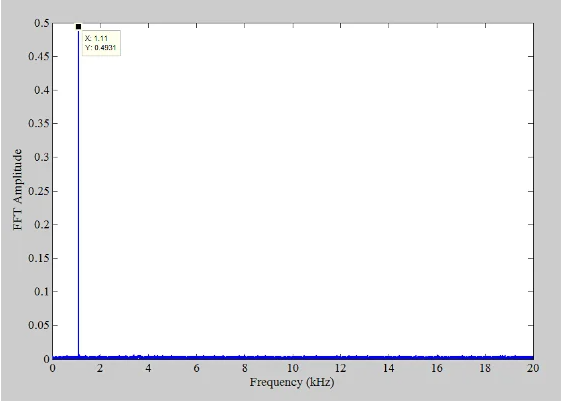
图6. f的抖动系统的谱s = 40 kHz。

施加抖动时，输入频率处只有一个显性分量。现在我们已经熟悉了抖动的功能，让我们来看看应用这种技术的不同方法。 

抖动方法：减法和非减法抖动

这两种抖动方法如图 7 所示。

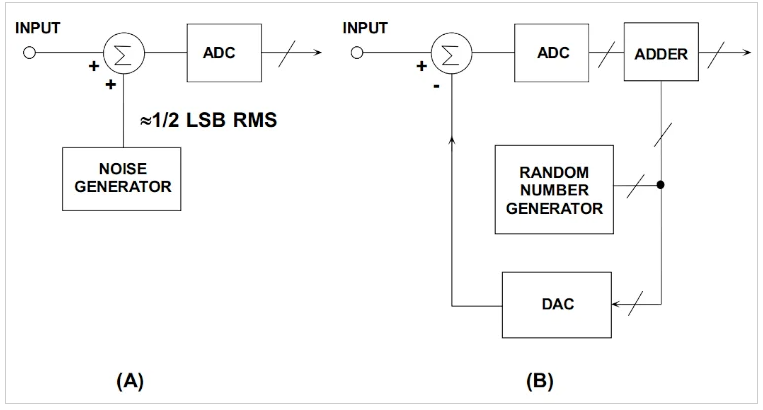
图7. （a） 非减法和 （b） 减法抖动拓扑的简单细分。图片由 ADI公司

在减法（图7（b））中，引入输入端的噪声以相反的极性添加到输出端，从而将系统输出端的净抖动噪声归零。通过图7（b）所示的特定实现，噪声发生器的输出被转换为模拟值并从输入中减去，而噪声的数字等效值则通过加法器添加到输出中。在非减法中，噪声被引入输入，而不从输出中减去。

正如我们稍后将讨论的那样，减法抖动可能比非减法版本更强大，尤其是在处理量化失真时。然而，在许多实际情况下，不可能仅仅因为抖动噪声在数字域中是未知的，就不可能从输出中减去抖动信号。

减法抖动 — 消除量化失真

抖动背后的理论相对复杂且需要数学密集型。在这里，在不通过数学细节的情况下，我们将看一下一些结果。如前所述，我们应该记住，减法抖动比非减法方法更强大。对于任意输入信号，可以证明具有适当抖动噪声的减法系统可以呈现白色的量化误差，在统计上与系统输入无关，并且在（-frac{LSB}{2}）到（+frac{LSB}{2}）范围内具有均匀分布。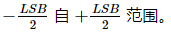

使量化噪声具有这些所需特征的一个抖动信号是白噪声，其均匀分布在（-frac{LSB}{2}）到（+frac{LSB}{2}）范围内。

非减法抖动 — 减少量化失真

对于任意输入，非减法拓扑不能使总误差均匀分布或在统计上独立于输入。然而，一个设计得当的非减法系统仍然可以大大改善量化系统。我们在本文第一部分中提供的仿真结果对应于非减法系统。这些模拟证实了非减材系统的有效性。

在正确选择抖动信号的情况下，非减法拓扑的总误差功率P错误，总计 可以通过公式1表示（有关更多详细信息，请参阅上一节中提到的书）。

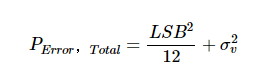
等式 1.

上述等式中的第一个项是众所周知的 理想量化器的噪声功率.第二项是抖动噪声的方差。公式1直观地有意义，因为它表明抖动噪声功率与量化噪声功率相加，从而决定了整个系统的本底噪声。如果我们使用方差较大的抖动噪声，则输出噪声水平会增加。换句话说，通过将抖动噪声添加到输入中，我们试图打破量化噪声和输入之间的相关性，但代价是略微提高了本底噪声。 

常见抖动信号

抖动信号的一个重要特征是其概率密度函数。具有高斯、矩形或三角形分布的抖动信号用于不同的应用。可用于减少非减法系统量化失真的矩形和三角形抖动信号如图9所示。

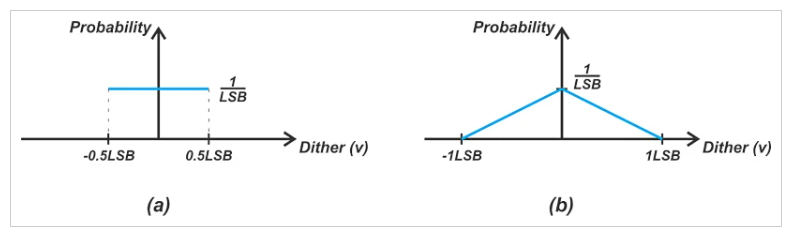
图9. （a）矩形和（b）三角形抖动信号的图，用于消除量化失真。

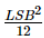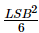上述矩形和三角形抖动信号的方差分别为（frac{LSB^{2}}{12}）和（frac{LSB^{2}}{6}）。 和分别。

对于高斯抖动，建议的方差为 （frac{LSB^{2}}{4}）。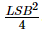

通过代入公式1中的这些值，我们可以计算出不同抖动类型的本底噪声增加。与无抖动系统相比，应用矩形、三角形和高斯抖动可以使非减法系统的本底噪声分别增加3 dB、4.8 dB和6 dB。