

MATLAB学习笔记之模糊算法2
电子说
描述
1.1.6 模糊推理的运用

1.2.7 模糊控制系统的组成

与一般的计算机控制系统不同的是,模糊控制系统的控制器是模糊控制器,模糊控制器是基于模糊条件语句描述的语言控制规则,又称为模糊语言控制器。
输入输出变量
(1)模糊控制的输入变量通常取E或E,EC或E,EC,ER,分别构成所谓的一维,二维,三维模糊控制器,一般选择控制量的增量作为模糊控制器的输出变量。
(2)描述模糊控制器的输入,输出变量状态:负大(NB),负中(NM),负小(NS),零(O),正小(PS),正中(PM),正大(PB)。
(3)描述误差变量的词集一般取为:负大(NB),负中(NM),负小(NS),负零(NO),正零(PO),正小(PS),正中(PM),正大(PB)。
模糊变量E的赋值表
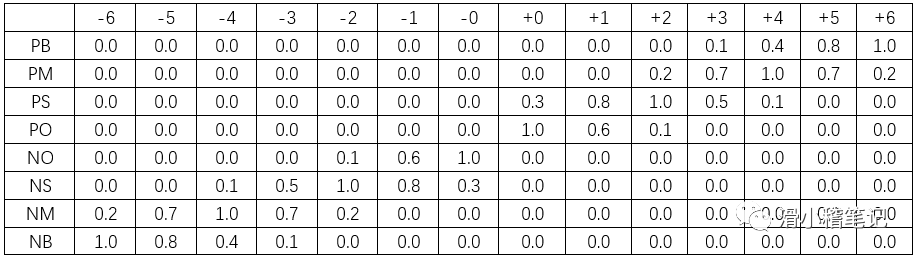
模糊控制规则
(1)条件语句的基本类型为:if A or B and C or D then E
例如水温控制规则之一为:若水温高或偏高,且温度上升快或较快,则加大冷水流量。
用条件语句表达为:if E=NB or NM and EC=NB or NM then U=PB
1.2.8 模糊控制算法的工程实现
在大型的模糊控制系统中常采用软件模糊推理法,模糊关系,模糊推理以及模糊判决的运算可以离线进行,最后得到模糊控制器输入量的量化等级E,EC与输出量即系统控制量的量化等级U之间的确定关系,这种关系通常称为控制表。
1.3 水位控制系统
1.3.1 控制目标
控制模型如下图所示,控制进水阀S1和出水阀S2,使水箱水位保持在目标水位O处。
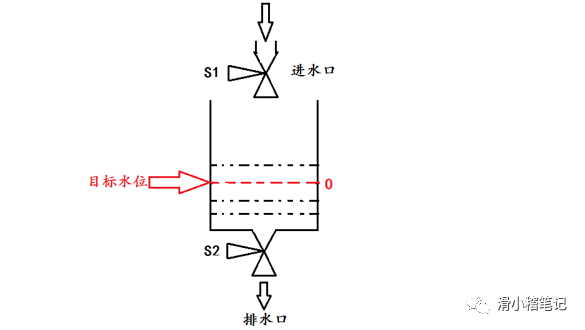
1.3.2 控制规则
(1)若当前水位高于目标水位,则向外排水,差值越大,排水越快
(2)若当前水位低于目标水位,则向内注水,差值越大,注水越快
(3)若当前水位和目标水位相差很小,则保持排水速度和注水速度相等
注:建立模糊控制规则的基本思想:当误差大或较大时,选择控制量应该以尽快消除误差为主,而当误差较小时,选择控制量要防止超调,以系统的稳定性为主要出发点。
1.3.3 控制步骤
(1)我们选择目标水位和当前水位的差值e作为观察量,选取阀门开度u为控制量。
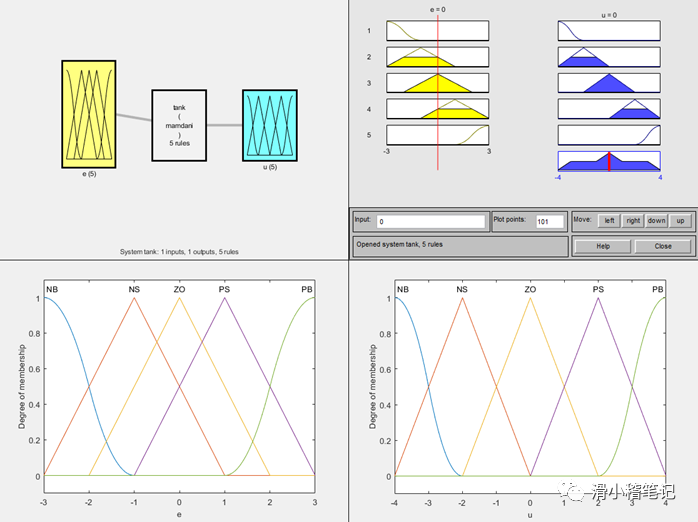
(2)将偏差e划分为5个模糊集,负大(NB)、负小(NS)、零(ZO)、正小(PS)、正大(PB),e为负表示当前水位低于目标水位,e为正表示当前水位高于目标水位。设定e的取值范围为[-3,3],隶属度函数如下图所示。
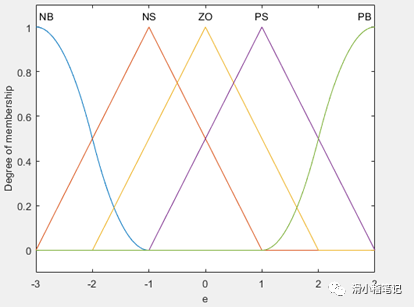
此时偏差e对应的模糊表如下表所示。
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|---|
| PB | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 |
| PS | 0 | 0 | 0 | 0.5 | 1 | 0.5 | 0 |
| ZO | 0 | 0 | 0.5 | 1 | 0.5 | 0 | 0 |
| NS | 0 | 0.5 | 1 | 0.5 | 0 | 0 | 0 |
| NB | 1 | 0.5 | 0 | 0 | 0 | 0 | 0 |
(3)将控制量u划分为5个模糊集,负大(NB)、负小(NS)、零(ZO)、正小(PS)、正大(PB),u为负表示增大进水阀门S1的开度(同时减小出水阀门S2的开度),u为正表示减小进水阀门S1的开度(同时增大出水阀门S2的开度)。设定u的取值范围为[-4,4],隶属度函数如下。
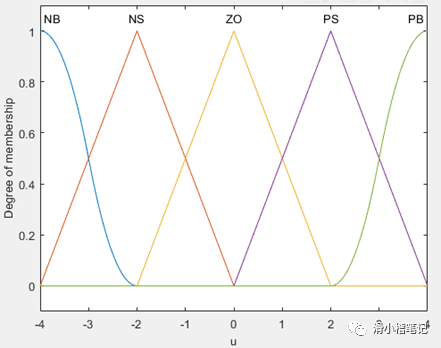
此时控制量u对应的模糊表如下表所示。
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|---|---|---|---|
| PB | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 |
| PS | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 | 0.5 | 0 |
| ZO | 0 | 0 | 0 | 0.5 | 1 | 0.5 | 0 | 0 | 0 |
| NS | 0 | 0.5 | 1 | 0.5 | 0 | 0 | 0 | 0 | 0 |
| NB | 1 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
(4)制定模糊规则:模糊规则的制定是模糊控制的核心内容,控制性能的好坏很大程度上由模糊规则决定,目前主要是根据经验来制定相应的规则
若e负大,则u负大
若e负小,则u负小
若e为零,则u为零
若e正小,则u正小
若e正大,则u正大
(6)进行模糊决策:最终需要的控制量u即为模糊控制的输出,u可由偏差矩阵e和模糊关系矩阵R合成得到
(7)控制量的反模糊化
我们模糊决策得到的控制量u是一个矩阵,并不能直接应用在工程上,因此需要将u解释为实际中的特定行为,即反模糊化操作。目前常用的反模糊化方法有以下几种:
最大隶属度法:应用于计算简单控制要求不高场合
重心法:可以使得输出更平滑
加权平均法:工业上应用最广泛
1.4 模糊控制算法实现
1.4.1 MATLAB代码
clc
clear
%创建模糊控制器
a = newfis('fuzzy tank');
%输入变量
a = addvar(a,'input','e',[-3,3]); %设置变量e为输入且定义域[-3,3]
a = addmf(a,'input',1,'NB','zmf',[-3,-1]); %Z型隶属度函数
a =addmf(a,'input',1,'NS','trimf',[-3,-1,1]); %三角形隶属度函数
a =addmf(a,'input',1,'ZO','trimf',[-2,0,2]); %三角形隶属度函数
a =addmf(a,'input',1,'PS','trimf',[-1,1,3]); %三角形隶属度函数
a = addmf(a,'input',1,'PB','smf',[1,3]); %S型隶属度函数
%输出变量
a = addvar(a,'output','u',[-4,4]); %设置变量u为输出且定义域[-4,4]
a = addmf(a,'output',1,'NB','zmf',[-4,-2]); %Z型隶属度函数
a =addmf(a,'output',1,'NS','trimf',[-4,-2,0]); %三角形隶属度函数
a =addmf(a,'output',1,'ZO','trimf',[-2,0,2]); %三角形隶属度函数
a =addmf(a,'output',1,'PS','trimf',[0,2,4]); %三角形隶属度函数
a = addmf(a,'output',1,'PB','smf',[2,4]); %S型隶属度函数
%建立模糊规则
rulelist=[1 1 1 1;
2 2 1 1;
3 3 1 1;
4 4 1 1;
5 5 1 1];
a = addrule(a,rulelist);
%设置反模糊化算法
a1 = setfis(a,'DefuzzMethod','mom'); %采用最大隶属度平均法进行反模糊化
writefis(a1,'tank'); %保存tank文件
a2 = readfis('tank'); %读取tank文件
%绘制图像
figure(1); plotfis(a2); %绘制模糊控制器结构
figure(2); plotmf(a,'input',1); %绘制输入隶属度函数图像
figure(3); plotmf(a,'output',1); %绘制输出隶属度函数图像
%打开模糊调试器
showrule(a);
ruleview('tank');
-
MATLAB学习笔记之模糊算法12023-02-27 3955
-
基于深度学习的图像去模糊算法及应用2022-10-28 4082
-
PID算法学习笔记分享2022-01-14 905
-
求大佬分享MatLab的学习笔记2021-11-19 1291
-
OpenStack之Cinder学习笔记2021-09-23 883
-
流形学习LLE算法的配套Matlab源码汇总2021-08-25 906
-
PID算法之模糊PID 精选资料推荐2021-07-19 2035
-
算法图解学习笔记分享2020-06-05 1521
-
FCM聚类算法以及改进模糊聚类算法用于医学图像分割的matlab源程序2018-05-11 3736
-
基于模糊高斯学习策略的粒子群进化融合算法2017-11-27 757
-
模糊推理的Mamdani算法及其Matlab实现2015-11-17 1510
-
模糊PID控制及其MATLAB仿真2015-11-12 1381
-
matlab之dsp学习2013-07-05 9458
全部0条评论

快来发表一下你的评论吧 !

