MATLAB学习笔记之模糊算法3

1.4.2 C语言代码

#include 
#include 
#include 
#define  N  7                      //定义量化论域模糊子集的个数
//模糊语言定义
#define  NB  -3
#define  NM  -2
#define  NS  -1
#define  ZO  0
#define  PS  1
#define  PM  2
#define  PB  3
struct
{
  //规则表
  int rule[ N ][ N ] ;                //模糊规则表
  //隶属度函数
  char *f_type_e ;                  //e的隶属度函数类型
  char *f_type_de ;                  //de的隶属度函数类型
  char *f_type_u ;                  //u的隶属度函数类型
  float paras_e[ 3*N ] ;                //e的隶属度函数的参数
  float paras_de[ 3*N ] ;              //de的隶属度函数的参数
  float paras_u[ 3*N ] ;                //u的隶属度函数的参数
  //模糊运算参数
  float Ke ;                    //Ke=n/emax,量化论域为[-3,-2,-1,0,1,2,3]
  float Kde ;                    //Ke=n/demax,量化论域为[-3,-2,-1,0,1,2,3]
  float Ku ;                    //Ke=umax/n,量¢化论域为[-3,-2,-1,0,1,2,3]
  float umax ;                    //输出的上限
  float emax ;                    //误差基本论域上限
  float demax ;                    //误差变化率基本论域的上限
  //控制目标参数
  float target ;                  //控制目标
  float actual ;                  //实际值
  float e ;                    //误差
  float e_pre ;                    //上一次的误差
  float de ;                    //误差的变化率
}_fuzzy_;
/*******************************************************
Name      :trimf
Function    :三角隶属度函数
Parameter  :
      x:自变量
      (a,b,c):定义域
Return    :结果
*******************************************************/
float trimf( float x, float a, float b, float c )
{
  float u ;
  if( ( x>=a )&&( x<=b ) )
    u = ( x-a )/( b-a ) ;
  else if( ( x>b )&&( x<=c ) )
    u = ( c-x )/( c-b ) ;
  else
    u = 0 ;
  return u ;
}
/*******************************************************
Name      :gaussmf
Function    :正态隶属度函数
Parameter  :
      x:自变量
      ave:均值
      sigma:方差
Return    :结果
*******************************************************/
float gaussmf( float x, float ave, float sigma )
{
  float u ;
  if( sigma<0 )
    printf("方差不允许小于0\\n");
  else
    u = exp( -pow( ( ( x-ave )/sigma ), 2 ) ) ;
  return u ;
}
/*******************************************************
Name      :trapmf
Function    :梯形隶属度函数
Parameter  :
      x:自变量
      (a,b,c,d):定义域
Return    :结果
*******************************************************/
float trapmf( float x, float a, float b, float c, float d )
{
  float u ;
  if( ( x>=a )&&( xelse if( ( x>=b )&&( x

**
最终代码运行结果如下图所示。

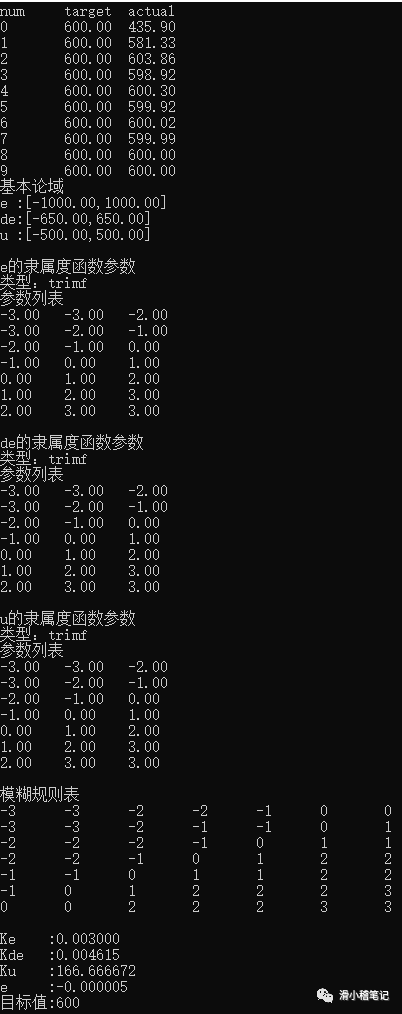
参考于CDSN

**