

代码实现密度聚类DBSCAN
描述
一提到密度聚类,脑海中立马就能呈现出一个聚类结果图,不自然的就感觉非常的简单,不就是基于密度的聚类嘛,原理不用看也懂了,但是真的实现起来,仿佛又不知道从哪里开始下手。这时候再仔细回想一下脑海中的密度聚类结果图,好像和K-means聚类的结果图是一样的,那真实的密度聚类是什么样子的呢?看了西瓜书的伪代码后还是没法实现?今天小编就带大家解决一下密度聚类的难点。
实现一个神经网络,一定一定要先明白这个网络的结构,**输入是什么?输出是什么?网络的层级结构是什么?权值是什么?每个节点代表的是什么?网络的工作流程是什么?**
对于密度聚类,有两个关键的要素,一个是密度的最小值,另一个是两个样本之间的最大距离。规定了密度最小值就规定了核心样本邻域包含数据的最小值,规定两个样本之间的最大距离就规定了两个样本相聚多远才算是一类。而且,这两个值都是需要不断测试之后才选取的,并不是一次就那么容易定下来的。另一个需要了解的就是,密度聚类中有 **核心对象、密度直达、密度可达、和密度相连** ,这几个概念。
核心对象就是指的一个类的核心,满足两个条密度聚类的关键要素,初始的核心对象有很多,但是经过不断迭代整合后,核心对象越来越少,到最后一个类形成后,核心对象就是一个抽象的概念,并不能明确的指出这个类的核心对象是哪一个,但一定是初始核心对象中的一个。初始的核心对象的邻域中,一定包含多个核心对象。
用下图来区分密度直达,密度可达和密度相连,假设X1为核心对象,那么X1和X2密度直达,X1和X3是密度可达,X3和X4是密度相连。密度相连就是两个相聚比较远的边缘节点了,密度直达和密度可达距离都比较近。
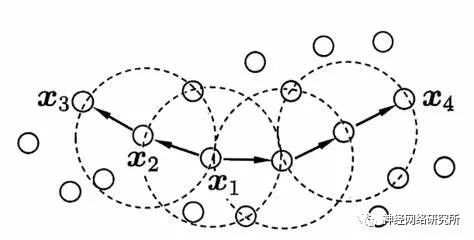
我们先理清一下密度聚类的过程:
- 首先要找到核心对象,即满足周围数据距离小于密度最小值的数据数量大于密度最小值,并且记录下核心对象的邻居节点。
- 随机选取一个核心对象,找到对应的邻居节点,即密度直达的节点,查看邻居节点中包含的核心对象,将这几个节点记录下来,并在核心对象列表中删除包含的核心对象,然后依次遍历这几个核心对象和它们的邻居,按照相同的方法,记录下的就是密度可达的节点。在遍历开始时,添加一个判断条件,判断这个节点是不是满足核心节点的条件,如果不满足,那么就不再查找它的邻域,这些节点就是密度相连节点,也就是这一个类的边缘节点。
下面就是整个密度聚类的代码:
#密度聚类
import numpy as np
import random
import time
import copy
np.set_printoptions(suppress=True)
def euclidean_distance(x, w): # 欧式距离公式√∑(xi﹣wi)²
return round(np.linalg.norm(np.subtract(x, w), axis=-1),8)
def find_neighbor(j, x, eps):
N = list()
for i in range(x.shape[0]):
temp = euclidean_distance(X[i],X[j]) # 计算欧式距离
print(str(j)+"到",str(i)+"的距离",'%.8f' % temp)
if temp <= eps:
N.append(i)
return set(N)
def DBSCAN(X, eps, min_Pts):
k = -1
neighbor_list = [] # 用来保存每个数据的邻域
omega_list = [] # 核心对象集合
gama = set([x for x in range(len(X))]) # 初始时将所有点标记为未访问
cluster = [-1 for _ in range(len(X))] # 聚类
for i in range(len(X)):
neighbor_list.append(find_neighbor(i, X, eps))
if len(neighbor_list[-1]) + int(count_matrix[i]) >= min_Pts: #如果权值对应位置的数据样本数量和相似权值的数量之和大于一定的数
omega_list.append(i) # 将样本加入核心对象集合
omega_list = set(omega_list) # 转化为集合便于操作
while len(omega_list) > 0:
gama_old = copy.deepcopy(gama) #上一状态未访问的节点
j = random.choice(list(omega_list)) # 随机选取一个核心对象
k = k + 1 #第几个类别
Q = list()
Q.append(j) #选出来的核心对象
gama.remove(j) #标记为访问过
while len(Q) > 0:#初始Q只有一个,但是后面会扩充
q = Q[0]
Q.remove(q) #把遍历完的节点删除
#正是下面这一个if决定了密度聚类的边缘,不满足if语句的就是密度相连,满足就是密度直达或者密度可达
if len(neighbor_list[q]) >= min_Pts:#验证是不是核心对象,找出密度直达
delta = neighbor_list[q] & gama #set的交集,邻域中包含的未访问过的数据
deltalist = list(delta)
for i in range(len(delta)):
Q.append(deltalist[i])#将没访问过的节点添加到队列
gama = gama - delta #节点标记为访问
Ck = gama_old - gama #记录这一类中的节点
Cklist = list(Ck)
for i in range(len(Ck)):
cluster[Cklist[i]] = k #标记这一类的数据
omega_list = omega_list - Ck #删除核心对象
return cluster
加载数据
X = np.load("文件位置")
X = X.reshape((-1,向量维度)) #修改维度
eps = 0.0000002 #两个样本之间的最大距离
min_Pts = 20 #样本的最小值
C = DBSCAN(X, eps, min_Pts)
C = np.array(C)
np.save("classify.npy",C)
print("C",C.reshape([X原来的维度]))
注意一点,密度聚类的输入数据,不管是多少维,用这个代码的话都要转换成一维数据再进行密度聚类。举个例子,二维数据row行,loc列,那么数据reshape成一维数据后,当前位置 i 对应的位置就是[(row*loc)+i]。如果有不懂或者有任何问题,欢迎留言讨论!
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
一种改进的基于密度聚类模糊支持向量机2009-03-20 575
-
基于DBSCAN的批量更新聚类算法2009-03-31 981
-
适用于公交站点聚类的DBSCAN改进算法2009-04-23 969
-
一种改进的基于密度聚类的入侵检测算法2009-08-24 508
-
基于网格的多密度聚类算法2009-08-27 1048
-
基于网格的快速搜寻密度峰值的聚类算法优化研究2017-11-21 1044
-
基于层次划分的密度优化聚类算法2017-12-17 891
-
基于密度差分的自动聚类算法2017-12-18 666
-
中点密度函数的模糊聚类算法2017-12-26 776
-
基于数据划分和融合策略的并行DBSCAN算法2018-02-08 1200
-
基于密度DBSCAN的聚类算法2018-04-26 22574
-
改进的DBSCAN聚类算法在Spark平台上的应用2021-04-26 1305
-
基于特征提取和密度聚类的钢轨识别算法2021-06-16 1551
-
10种聚类介绍和Python代码2022-07-30 7094
全部0条评论

快来发表一下你的评论吧 !

