

单目立体视觉:我用单目相机求了个体积!
电子说
描述
1、前言
最近弄了点小项目,关于单目立体视觉的,目的是对单目下的物体体积进行解算。对这件事我个人觉得这是一个很有意思的话题,查阅了一些相关的文章,做单目立体视觉的高校、公司都还很多。比如说2021年北方工业大学的一篇硕士论文中进行了与此相关的技术研究,如果没记错的话,清华大学做过辅助激光实现的立体圆柱体积测量,苏州大学也完成了类似的单目体积测量研究。当然目前也有很多的深度相机可能可以直接通过读数完成对目标的测量,但是对立体视觉的研究思考,空间的转换关系依然是一个重要的课题。
一般而言,单目是无法依靠自身来完成测量的,有企业选择让单目相机动起来,但是一旦动起来实际上也是双目,不再是单目。其实单目最大的问题是缺少了深度信息。近大远小是我们最常用的成像规律,近处物体在视场中占比大,远处物体在视场中占比小。因此,我们需要些方法来弥补缺失的深度信息。从硬件角度上可以辅佐以激光、结构光等等,这都是比较常用的辅助手段,三维成像上来说线结构光对扫描结构重构技术也已经相对比较完善了。因此在解决单目立体视觉问题下的辅助手段问题,我是打算将目标置于标准平台上,利用标准平台的数据来对相机进行标定,从而构建我需要的视场参数,进而求解。图1是我利用工业相机与镜头在一块标准平台的方块采集结果。在标准平台上,底面的洞洞空,空间距离为2.5 cm。

图1 实物图与采集现场
视觉测量中一般的步骤是图像采集、标定、目标提取、像素长度角度提取以及最后的实际长度解算过程。
有时候会觉得自己很耍赖,用工业相机加定焦镜头这种畸变很小的方式做图像测量实验很玩赖(还选了对图像处理最为有利的打光方式)~如果在要求精度不高的情况下,确实很容易得到无畸变下图像的具体尺寸,但是我又觉得逐步的提高精度,才是视觉测量该有的样子,相比于利用各种花式的测量方法,难道大家利用图像的原因不就是因为可以到1 um,2 um的测量精度与一整个平面的采集效果嘛~当然以上都是题外话的随笔,下面还要接着介绍一些标定求解的思路。

图2 目标背景点提取
2、部分理论分析
图2是目标背景点的提取情况,利用图像处理的手段将目标背景中的每一横行的纵向距离提取出来,从图像上也能看出来距离镜头近的地方两个横行之间距离长,距离镜头远的地方距离短,这是很符合近大远小的规律的。那么我到底要标定求解什么呢?
普适意义上的标定一般上都是遵循张氏标定法,将空间坐标系与图像坐标系之间的关系用矩阵的方式写出来,这其中主要是涉及到两个重要参数,一个是相机内参,一个是相机外参。内参数一般包括了相机的像元尺寸、相机的畸变情况;外参代表了相机与目标的空间位置。因此既然我能得到空间位置就一定可以得到成像平面的相关数据,那么体积的求解似乎就变得没那么难了。但是标定并不是一成不变的,不同位置的标定结果显然是不一样的,不同深度的标定结果也不一样,这其中就有人考虑,是不是可以把标定靶直接和目标粘连在一起?那么确实存在这样一种方案可以实现,这种方法叫合作目标标定测量。
而我想写下的是更基础一点的一些标定思路,我也是在没有用张氏标定法情况下用固定平面作为标定靶来做体积测量。
我分析了一些问题,首先,近大远小的根本原因是什么?在不考虑畸变的前提下,我觉得是因为在相机深度范围内,物距变大了,导致光学放大倍数变小了,或者说单个像元的尺寸当量变大了。远处尺寸当量大,那么相同像元个数下,视场变大,远处的目标在视场中占比就变小,近大远小,自此而来。那么第二个问题就来了,像元尺寸当量的变化规律是怎么样的呢?在张氏标定法中给出的旋转矩阵来看,好像是一次线性关系,那如何推导呢?第三个问题,实际上的像素尺寸乘以像素当量就是我要得结果了嘛?显然不是,还需要与我的镜头成像夹角有关系~
基于上一段的分析,我得出这样一些简单的思考结论:
(1)我默认了成像时没有畸变的,因此在求解上不考虑桶形畸变的补偿问题;
(2)我默认了相机在横向是没有变化的,或者说像素当量在横轴方向上是几乎不变的,也就是说,在图二中每一条横线上两个孔之间的距离基本是保持不变的,比如说距离镜头最近的一条红线上,每个孔之间的像素距离是近似不变的(事实上也确实基本不变);
(3)我需要求解在竖直方向上像素当量与距离的关系;
(4)我需要解算相机平面角度。
2.1 竖直像素当量与距离关系
竖直像素当量与距离的关系推演,应该从定焦镜头的焦距公式入手,式子中t代表像素当量。
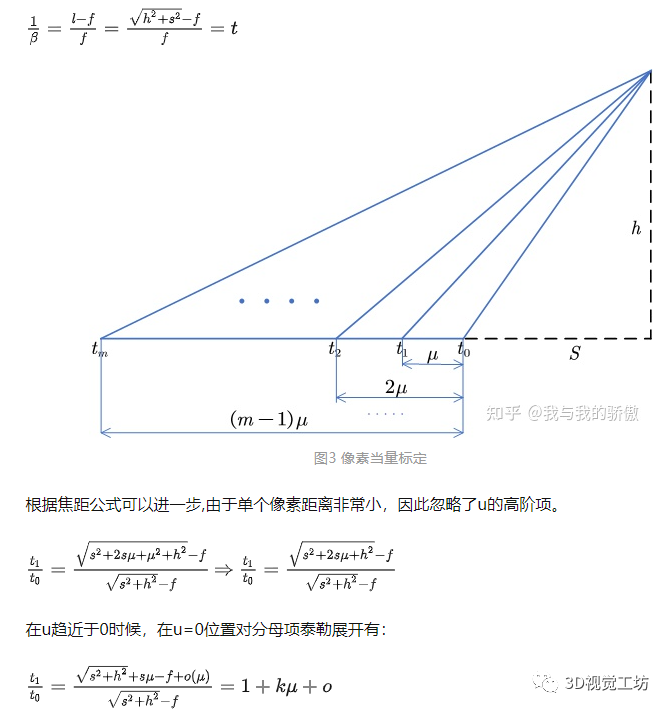
该式子表达了一个概念就是像素当量的比值是像素个数的线性递增关系。那么对于视场内任何一个位置的像素当量对最下测边缘像素当量的比值应该有:
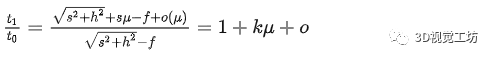
那么基于该公式就可以对底面坐标进行标定。图2中将每一横行的点连接在了一起,那么以最下测边缘为底边,前一条变距离最下测边缘距离为视场标定前lcm,并且,该lcm由有限个像素m组成,那么对这连续的像素分点进行建模,构建像元与实际尺寸之间的关系有:
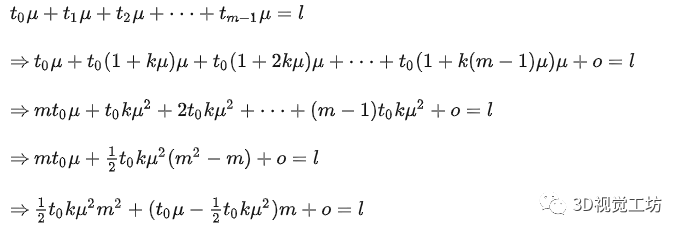
因此从上式可以反映出一个重要的推论,图像上任何一点到基准线(图2中最下测直线)的像素个数与实际距离间的关系为二次项关系。举一个例子,在上图2中一共有10条线,从上到下,第十条为基准线,第九条与第十条之间具有138个像素,此时真实距离为视角标定前的2.5cm;第八条与第十条之间具有138+125个像素,此时真实距离为视角标定前的5cm;第七条与第十条之间具有138+125+113个像素,此时真实距离为视角标定前的7.5cm。以此类推,就可以构建相关函数。
此处埋下一个伏笔,对于该部分的像素当量与距离之间的关系有两个需要注意的部分,一是我没有直接把像素个数与2.5,5,7.5这几个数直接拟合,因为这里面有一个视场角的问题,举个例子,一个东西长10cm,但是你用斜着的视场去看的时候,这个东西肯定没有10cm,这部分我会在下一部分中给出介绍;另一个伏笔,前面关系式子中m的二次项与一次项系数相加实际上就是基准线上的视场距离。
2.2 视场角解算
视场角解算是一个很有意思的问题。我不记得我在前一篇文章中是否解释过这个问题,但是这里面确实就是这样,一个物体在倾斜相机上的投影会导致距离发生改变,如图3所示。
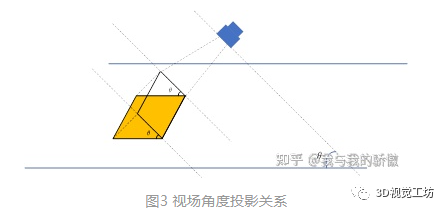
这也是我在2.1最后说的第一个伏笔,两条线之间的2.5cm在投影到相机成像平面后不会再是2.5cm了,应该是其乘以视场角的余弦值。这也是为什么我不直接在2.1中给出直接拟合的原因。那么如何求解这个视场倾角呢?这里面我思考了很多,甚至一度想直接给固定值算了,但是我又觉得这很不靠谱,一定有什么办法能够推出视场角。后来,我想到了这个图4。
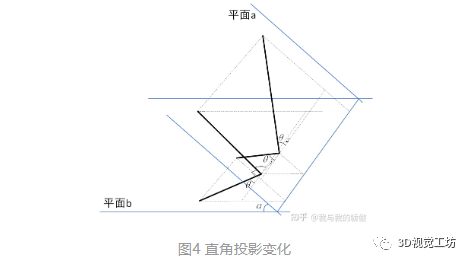
图4中直角三角形在斜面投影过程中,直角三角形变成了钝角三角形,究其原因是投影后平行于平面交线方向大小不变,垂直于交线方向变小,因此直角边合投影的角度变大,两条直角边的角度都变大,导致投影后角度大于90°。因此,依靠立方体的角度变化可以反演投影面夹角。经过分析发现一个问题, 如果直角的两条边分别垂直和平行于两个平面的交线,那么直角角度并不发生改变,因此在图4中有如下的关系:

因此在已知投影后与投影交线的夹角可以解算两个平面夹角有:

tanθ1tanθ2=cos2α 2.3 横向像素当量与数值距离关系
在理解横向像素当量问题前先回忆一下2.1中的纵向像素当量问题,纵向像素当量随着距离变化规律是一个二维函数规律,随着目标点到基准线距离的变化,一个像素代表的实际距离呈规律性变化。在忽略了横向畸变情况下,每一行的横向当量也存在规律性变化。在给出基线上单个像素当量,与基线不同的距离得到的一维比例关系也应该符合与2.1中相同的一维线性公式。
3、求解
在单目下的立方体被投影成一个六边形。六边形中三条边为主要测量边,其中两条边在标准平面上。

图6 边缘提取
标准平面上的两条边有以下两个目的:
(1)根据夹角计算镜头成像夹角。标准直角在镜头投影后变成钝角,利用2.2的视场解算方法可以得到镜头与平面夹角;
(2)将平面上两条边分别按照竖向与横向进行分解,横向与竖向上的分解结果根据像素数量分别代入2.1与2.2的系数公式计算真实长度。
图2中背景底线将用于获得二次项拟合系数矩阵。
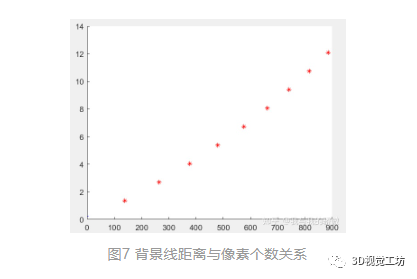
根据图7获取的系数矩阵有[6.63840796147980e-06,0.00750901860528093,0.215679358071086]。
利用系数矩阵代入可以获取的长度为4.65009与6.36081。
最后是利用高度特征边获取高度的计算,高度的计算是一个逆向过程,图3中从出发点到最远点,镜头到点的距离越来越远,当量越来越小;但是由于竖直高度原因,高度上的点,越向上反而离镜头越近,也就是此时的当量越来越大。与前文中的一次型相反,在高度的计算当量越来越大就可以实现高度的反演。
利用该方法获取的高度为2.88764。
利用千分尺获取的三条边长度分别为4.6、6.4与2.8cm。
4、总结
做一个简单的总结。
首次接触该项目是一个在22年年初,大概3月份就完成了整体方案方法的设计,本想着早一些把利用单目方法获取图像计算体积的一次尝试写在知乎文章里,但是拖延症一拖再拖到22年年底的圣诞节。
评价整体的方案方法来说,全文其实就提出了一个概念,就是利用泰勒展开消去高阶项得到的像素当量与标准距离之间的二次项关系。其实方法来说科学性并不是非常足,尤其是利用该特点反推待测物高度时候,应该说,这是单目需要重点解决的问题之一,但是我在文中涉及到的方法有一些草率。
单目视觉到底有没有应用价值呢?从需求来看,在给机场的箱体包裹计算、快递的包裹大小计算上其实还是有意义的,而且在方便人工测量分拣上还是有价值的。
单纯依靠单目视觉是无法处理深度问题的,虽然现在也设计推出了很多深度相机,但是深度相机的应用对象并不是对目标做三维反演。所以单目视觉需要搭配其他标准物来实现标定测量,而且这个标准物一定要出现在视场中,该文的光学平台就是系统的标定物,这或许可以为单目视觉测量提供一种思路。
当前的标定与反演方法来说,还是要依靠涨势标定法,张氏标定法具有非常高的普适性,但是在处理特殊问题上,确实可以用更多的方法实现标定的简化,这也是我在全文中写了这么多的目的。
最后,该项目来源于某校的本科毕业设计,根据毕业设计上的评语认为该方法在处理上具有特殊性,但是我采用同样的程序跑了几个差不多的立方体得到的数据结果还是蛮符合千分尺的测量结果,我个人会认为虽然方法草率了些,但是适用性,在光学平台上放置立方体的测量结果我还是很认可的。
最后的最后,如果有人能认真阅读,我真的会非常感谢各位的指正~!单目立体视觉完全是个人爱好,抽空拿出来做了一点算法的研究,如果有需要,相关利用Halcon完成的代码完全可以开源。再拜谢。
审核编辑 :李倩
-
中科慧眼三目立体视觉产品的功能优势2025-05-06 1233
-
中科慧眼三目立体视觉相机将亮相2025上海车展2025-04-19 1174
-
双目立体视觉是什么?单目视觉与双目立体视觉的区别?2023-08-17 6011
-
基于单目立体视觉的视觉测量步骤2022-12-27 2314
-
如何使用FPGA实现微型实时多目立体视觉机的设计2021-04-02 1057
-
如何使用FPGA实现三目立体视觉外极线校正的方法2021-04-01 1236
-
双相机立体视觉和结构光立体视觉原理及优势对比2019-05-14 8813
-
基于双目立体视觉的桥梁裂缝测量2018-01-16 1362
-
遗传算法的单目相机标定2018-01-05 856
-
三目立体视觉外极线校正及其FPGA实现方法2016-09-17 705
-
微型实时多目立体视觉机设计与实现2016-09-14 491
-
双目立体视觉原理大揭秘(一)2013-11-21 3206
全部0条评论

快来发表一下你的评论吧 !

