直流电路及波形讲解

电路理论中使用最多的交流波形是正弦波或正弦波。 电压源形式的周期性 AC 波形产生 EMF，其极性定期反转，完成一次完全反转所需的时间称为波形周期。

直流电或更常见的DC是一种电流或电压形式，仅在一个方向上围绕电路流动，使其成为“单向”电源。

通常，直流电流和电压均由电源、电池、发电机和太阳能电池等产生。 直流电压或电流具有固定的幅度（振幅）和与之相关的确定方向。 例如+12V代表正向12伏，-5V代表负向5伏。

我们还知道，直流电源不会随时间改变其值，它们是在连续稳态方向上流动的恒定值。 换句话说，DC 始终保持相同的值，并且恒定的单向 DC 电源永远不会改变或变为负值，除非其连接在物理上被反转。 下面显示了一个简单的 DC 或直流电路的示例。

直流电路及波形

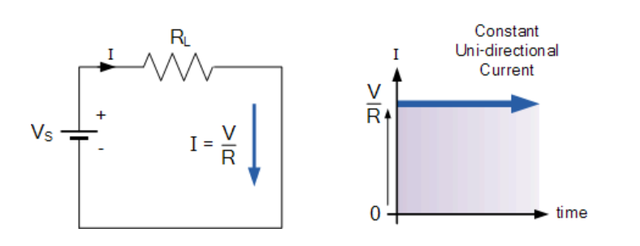
另一方面，交替函数或AC 波形被定义为在幅度和方向上以相对于时间或多或少均匀的方式变化的波形，使其成为“双向”波形。 交流函数可以表示电源或信号源，其交流波形的形状通常遵循数学正弦波的形状，定义为：A(t) = A max *sin(2πƒt)。

术语 AC 或对其交流电的完整描述，通常是指随时间变化的波形，其中最常见的被称为正弦波，更广为人知的是。 正弦波形通常被简称为。 正弦波是迄今为止电气工程中使用的最重要的交流波形类型之一。

通过绘制电压或电流的瞬时纵坐标值随时间变化而获得的形状称为交流波形。 交流波形每半个周期不断改变其极性，分别在时间上分别在正最大值和负最大值之间交替，一个常见的例子是我们在家中使用的家用电源电压。

这意味着交流波形是一种“时间相关信号”，最常见的时间相关信号类型是周期波形。 周期性或交流波形是旋转发电机的结果。 通常，任何周期波形的形状都可以使用基频生成，并将其与不同频率和幅度的谐波信号叠加，但那是另一个教程的内容。

交流电压和电流不能像直流电 (DC) 那样存储在电池或电池中，在需要时使用交流发电机或波形发生器生成这些量更容易和更便宜。 交流波形的类型和形状取决于产生它们的发生器或设备，但所有交流波形都包含一条零电压线，它将波形分成对称的两半。 的主要特征定义为：

交流波形特性

周期(T)是波形从开始到结束重复自身所用的时间长度（以秒为单位）。 这也可以称为正弦波波形的周期时间，或方波的脉冲宽度。

频率(ƒ)是波形在一秒内重复的次数。 频率是时间周期的倒数 ( ƒ = 1/T )，频率单位是赫兹(Hz)。

振幅(A)是以伏特或安培为单位测量的信号波形的幅值或强度。

在我们关于波形的教程中 ，我们查看了不同类型的波形并说“波形基本上是电压或电流变化的可视化表示，绘制为时间基准”。 通常，对于 AC 波形，这条水平基线表示电压或电流为零的情况。 位于水平零轴上方的 AC 型波形的任何部分都表示沿一个方向流动的电压或电流。

同样，位于水平零轴下方的波形的任何部分都表示沿与第一个方向相反的方向流动的电压或电流。 通常对于正弦交流波形，零轴上方的波形形状与其下方的形状相同。 然而，对于包括音频波形在内的大多数非电源交流信号，情况并非总是如此。

电气和电子工程中使用的最常见的周期信号波形是正弦波形。 然而，交流交流波形可能并不总是采用基于三角正弦或余弦函数的平滑形状。 交流波形也可以采用复波、方波或三角波的形状，如下所示。

周期波形的类型

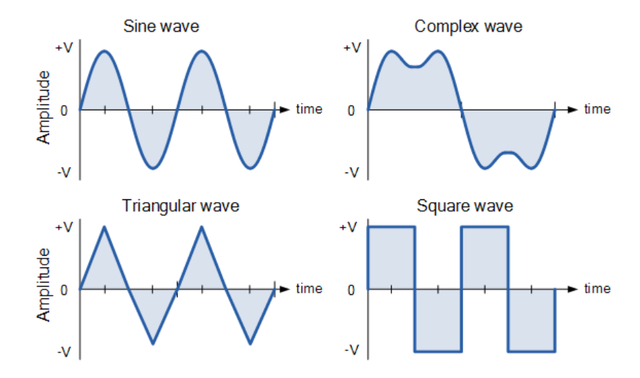
从其正半部分到负半部分并再次回到其零基线完成一个完整模式所花费的时间称为一个周期，一个完整的周期包含一个正半周期和一个负半周期。 波形完成一个完整周期所花费的时间称为波形的周期时间，并用符号“T”表示。

一秒内产生的完整周期数（周期/秒）称为频率 ，交变波形的符号ƒ。 频率的单位是赫兹，( Hz ) 是以德国物理学家海因里希·赫兹的名字命名的。

然后我们可以看到周期（振荡）、周期时间和频率（每秒周期数）之间存在关系，因此如果一秒内有ƒ个周期，则每个单独的周期必须花费1/ƒ秒才能完成。

频率与周期时间的关系

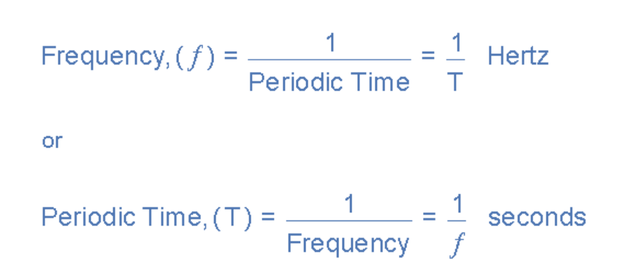
交流波形示例 No1

50Hz 波形的周期时间是多少？ 2. 周期时间为 10mS 的交流波形的频率是多少。

1).

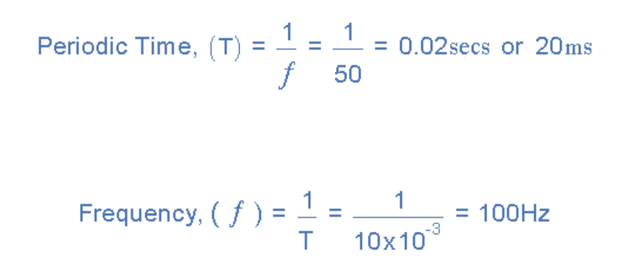
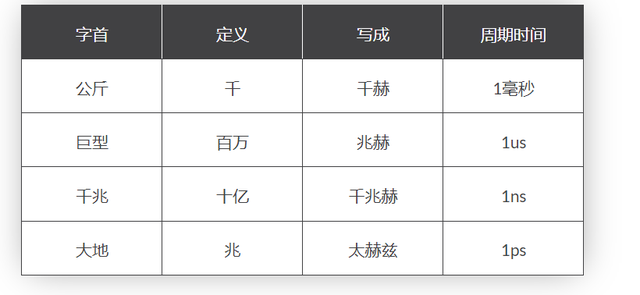
2).过去，频率以缩写为“cps”的“每秒周期数”表示，但现在更常用的单位是“赫兹”。 对于家用主电源，频率为 50Hz 或 60Hz，具体取决于国家/地区，并由发电机的转速决定。 但是一赫兹是一个非常小的单位，因此使用前缀表示波形在较高频率（例如kHz、MHz甚至GHz ）下的数量级。

频率前缀的定义

交流波形的幅度

除了了解交变量的周期时间或频率外，交流波形的另一个重要参数是振幅 ，更广为人知的是它的最大值或峰值，由项表示，V max表示电压，I max表示电流。

峰值是波形在从零基线开始测量的每个半周期内达到的电压或电流的最大值。 与可以使用欧姆定律测量或计算的具有稳定状态的直流电压或电流不同，交流量会随时间不断改变其值。

对于纯正弦波形，两个半周期 ( +Vm = -Vm )的峰值始终相同，但对于非正弦波形或复杂波形，每个半周期的最大峰值可能非常不同。 有时，交变波形被赋予一个峰峰值，V p-p值，这只是一个完整周期内最大峰值+V max和最小峰值-V max之间的距离或电压总和。

交流波形的平均值

由于直流电压恒定，因此连续直流电压的平均值或平均值将始终等于其最大峰值。 只有当直流电压的占空比发生变化时，该平均值才会发生变化。 在纯正弦波中，如果在整个周期内计算平均值，则平均值将等于零，因为正半部分和负半部分将相互抵消。 因此，仅在半个周期内计算或测量交流波形的平均值或平均值，如下所示。

非正弦波形的平均值

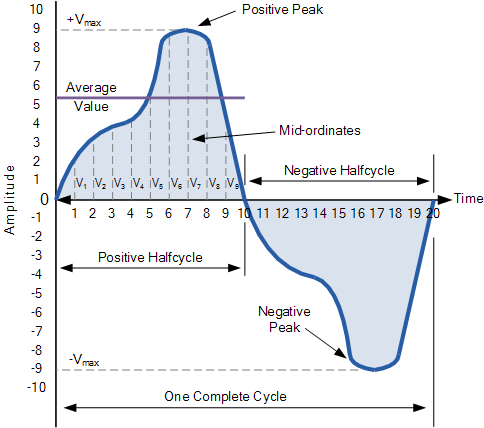
为了找到波形的平均值，我们需要使用数学中常见的中坐标规则、梯形规则或辛普森规则来计算波形下方的面积。 只需使用中坐标规则，就可以轻松找到任何不规则波形下的大致面积。

零轴基线被分成任意数量的相等部分，在我们上面的简单示例中，该值为九（V 1到 V 9 ）。 绘制的纵坐标线越多，最终平均值或平均值就越准确。 平均值将是所有瞬时值相加后除以总数。 这是给出的。

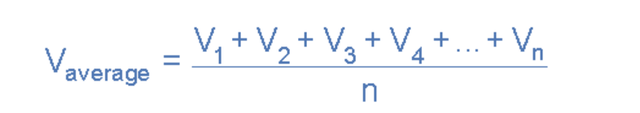
其中：n等于实际使用的中坐标数。

对于纯正弦波形，此平均值或均值将始终等于0.637*V max，并且此关系也适用于电流的平均值。

交流波形的有效值

我们上面计算的交流波形的平均值为：0.637*V max与我们用于直流电源的值不同。 这是因为与恒定且具有固定值的直流电源不同，交流波形会随时间不断变化并且没有固定值。 因此，为负载提供与直流等效电路相同的电功率的交流系统的等效值称为“有效值”。

正弦波的有效值在负载中产生相同的 I 2 *R 热效应，就像我们期望看到的相同负载是否由恒定直流电源供电一样。 正弦波的有效值通常称为均方根或简称为RMS值，因为它计算为电压或电流平方的均值（平均值）的平方根。

也就是说，V rms或 I rms是作为正弦波的所有平方中坐标值之和的平均值的平方根给出的。 任何 AC 波形的 RMS 值都可以从以下修改后的平均值公式中找到，如图所示。

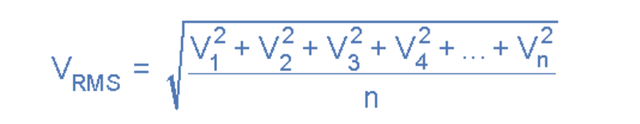
其中：n等于中坐标的数量。

对于纯正弦波形，此有效值或 RMS 值也始终相等：1/ √ 2 V max等于0.707V max，此关系适用于电流的 RMS 值。 除矩形波外，正弦波的 RMS 值始终大于平均值。 在这种情况下，热效应保持不变，因此平均值和 RMS 值将相同。

关于 RMS 值的最后评论。 除非另有说明，否则大多数万用表，无论是数字式还是模拟式，都只测量电压和电流的 RMS 值，而不是平均值。 因此，当在直流系统上使用万用表时，读数将等于I = V/R，对于交流系统，读数将等于Irms = Vrms/R。

另外，除平均功率计算外，在计算 RMS 或峰值电压时，仅使用 V RMS来计算 I RMS值，或使用峰值电压 Vp 来计算峰值电流 Ip 值。 不要将它们混合在一起，因为正弦波的平均值、RMS 或峰值是完全不同的，您的结果肯定是不正确的。

外形和波峰因数

尽管目前很少使用，但形状因数和波峰因数都可用于提供有关 AC 波形实际形状的信息。 形状因数是平均值与 RMS 值之间的比率，并给出为。

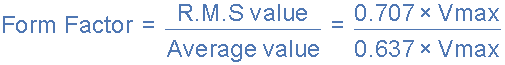
对于纯正弦波形，Form Factor 始终等于1.11。 波峰因数是 RMS 值与波形峰值之间的比率，给出为。

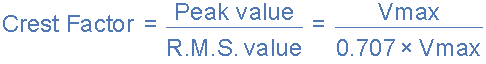
对于纯正弦波形，波峰因数始终等于1.414。

交流波形示例 No2

6 安培的正弦交流电流流过 40Ω 的电阻。 计算电源的平均电压和峰值电压。

RMS 电压值计算如下：

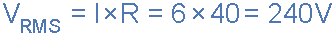
平均电压值计算如下：

峰值电压值计算如下：

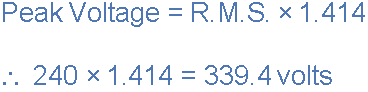
平均值、RMS、形状因数和波峰因数的使用和计算也可用于任何类型的周期波形，包括三角波、方波、锯齿波或任何其他不规则或复杂的电压/电流波形。 各种正弦波值之间的转换有时会令人困惑，因此下表提供了一种将一个正弦波值转换为另一个正弦波值的简便方法。

正弦波转换表

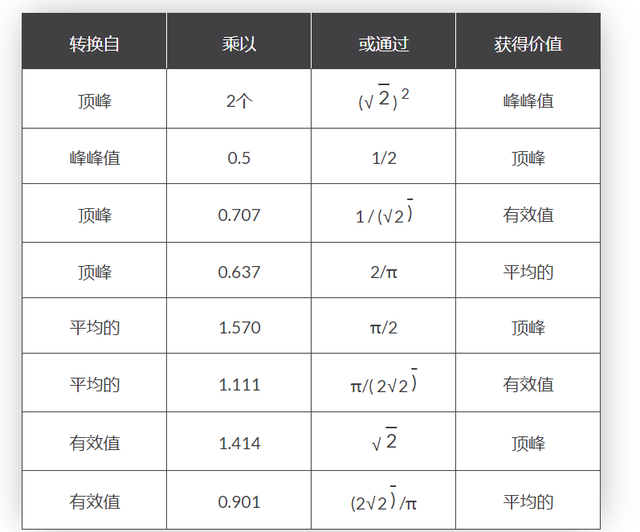
在下一个关于正弦波形的教程中，我们将了解生成正弦交流波形（正弦曲线）的原理及其角速度表示。