数字电路基础

1、数制的转换

由于计算机中无法识别十进制，所有的运算均是二进制运算，所以为了适应计算机的工作方式，就需要学会将十进制转换为二进制，这也是为了后续的程序设计打基础。

（1）十进制转二进制

十进制转二进制有两种方式，第一种便是常见的除2取余法，即将需要转换为二进制的数的整数部分进行除二，然后取其余数，即可得到整数部分的二进制数据，将小数部分采用乘2取整法获取小数部分的二进制数据，如下图所示。假定获取十进制数据102的二进制数据，步骤如下。

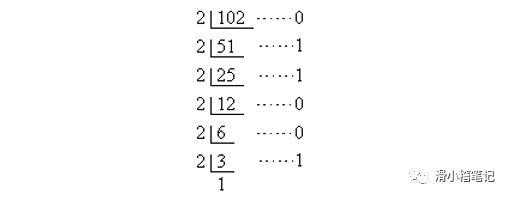
（2）二进制，八进制，十六进制互相转换

之前学习了十进制转换二进制的方法，二进制转换八进制与十六进制就已经非常简单了，将二进制三位一组，不足三位自动补零，将每一组二进制均换成十进制就是八进制数据；而二进制四位一组，不足四位自动补零，将每一组二进制均换成十六进制表示就是十六进制数据，其中十六进制的0~9和十进制一样，但是10~15在十六进制则是用ABCDEF表示，例将二进制1100010101转换为八进制和十六进制的步骤如下：

八进制：1100010101—>001100 010 101—>1425，即八进制数据为1425；

十六进制：1100010101—>00110001 0101—>315，即十六进制数据为315。

注：为了区分十进制，八进制，二进制与十六进制，通常在数据后面加上对应的符号，二进制用B表示，八进制用O表示，十六进制则用H表示，十进制一般默认不需要英文字母表示。上述例子中的八进制1425即可表示为1425 O，十六进制315则可表示为315 H，二进制1100010101则可以表示为1100010101 B。

（3）十进制与二进制，八进制，十六进制的转换步骤

若非十进制转二进制，八进制，十六进制可以直接分组转换，若十进制转换为其余几个进制，则一般现将十进制转换为二进制后再转其他进制。

2、几种常见的编码

（1）8421BCD码：8421BCD码是一种将十进制的每一位分别用四位二进制表示的一种数字编码。

（2）格雷码：又称为循环码格雷码最大的优点就是在按照编码顺序时，相邻两个代码之间只有一位发生变化，这样在代码转换的过程中就不会产生过渡“噪声”。

（3）ASCII码：即美国信息交换标准代码，采用7位二进制表示了常见的标点符号，数字，英文大小写和一些控制字符，一共128个。

上述的几种代码如下表所示

5、常用的门电路

6、逻辑代数基本公式

7、卡诺图化简

将n变量的全部最小项各用一个小方块表示，并使具有逻辑相邻性的最小项在几何位置上也相邻的排列起来，所得到的的图形称为n变量最小项的卡诺图。为了保证卡诺图中的几何位置相邻的最小项在逻辑上也具有相邻性，这些数码不能按自然二进制数从小到大的顺序排列，而必须按下图所示的方式排列，以确保相邻的两个最小项仅有一个变量使不同的

由于根据逻辑表达式生成的卡诺图可能会比较复杂，在实际的设计中可能会缺少某些门电路导致无法投入生产，所以需要根据卡诺图对函数表达式进行化简，已达到利用最少的元件完成功能的实现，这就是卡诺图化简的意义。例如化简如下图所示的卡诺图

8、逻辑函数的两种标准形式

9、补码，反码与原码