

电路分析基础-电路定理
描述
引言
本章节的知识是整个电路分析的基石,本章节所研究的节点电压法,回路电流法,网孔电流法,支路电流法覆盖了整个直流电路分析与交流电路分析,配合线性代数中的系数矩阵或增广矩阵的初等行变换,使电路的分析方法化为最简。
一、电路理论部分
1、支路电流法
(1)对于b条支路n个结点的电路,可以列写n-1个独立的电流方程,和b-n+1个独立的电压方程。
(2)例题分析
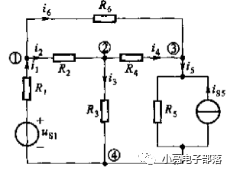
解析:图中共有结点4个,支路6条,故需要列写KCL方程3个,KVL方程3个。取结点①、②、③作为独立结点,取三个网孔作为回路,列写3个独立的KVL方程,故所列写的方程组为
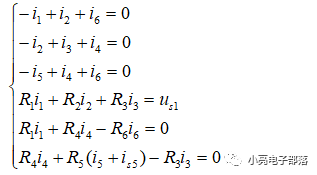
2、回路电流法
(1)取回路的电流作为研究对象,通过自阻与互阻的关系列写方程组。
(2)互阻:两个回路共有的电阻称为互阻,互阻电压的方向取决于两个回路中的电流的方向,若方向相反,则互阻取负值,若方向相同,则互阻取正值。
(3)自阻:回路中的电阻的和称为回路的自阻。
(4)电压的取值方向:按回路电流的绕行方向,箭头先碰到负极,则电压取正值,反之,电压取负值。
(5)例题分析
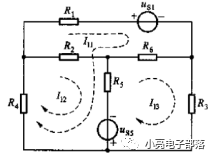
解析:根据回路电流的绕行方向可知,回路1的自阻为R1+R6+R5+R4,回路2的自阻为R2+R4+R5,回路3的自阻为R3+R5+R6,回路1和回路2的互阻为R4+R5,回路1和回路3的互阻为R5+R6,回路2与回路3的互阻为R5,且回路1与回路2的电流在流过互阻上的方向相同,回路1与回路3的电流在流过互阻上的方向相反,回路2与回路3的电流在流过互阻上的方向相反。故列写的回路电流方程为
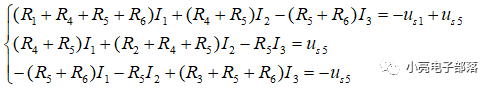
3、网孔电流法
网孔电流法是回路电路法的特例,将回路电流法中的取回路绕行方向改为取网孔绕行方向即可。
4、节点电压法
(1)以节点电压为研究对象,主要研究结点对于参考节点的电压,通过自导与互导的关系列写方程组。
(2)注意:若支路中有电流源与电阻的串联,则该支路可以直接去掉。
(3)自导:连接在某个节点上的所有电导的和。
(4)互导:位于两个节点上的电导的和,方程中一律取负值。
(5)例题分析
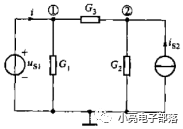
解析:根据结点的位置可知,结点1的电压为电压源Us1的电压,结点2的自导为G2+G3,结点1与结点2的互导为G3,流入结点2的电流为电流源Is2的电流,故列写的节点电压方程为
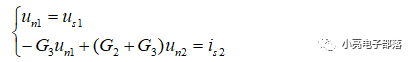
5、叠加定理
(1)叠加定理适用于线性电路的分析,对于多个电源的电路,输出的电压等于各自电源单独作用时的代数和。在分析时,先将一个电源单独作用,其余的电源变为0,即电压源短路,电流源开路。
(2)例题分析
求解图中的电流I2。
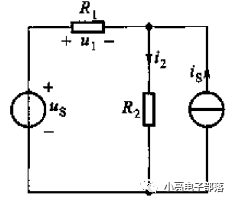
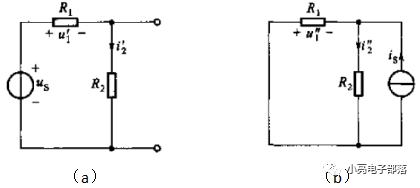
解析:首先令电压源单独作用,等效电路如图a所示,其次令电流源单独作用,等效电路如图b所示,故
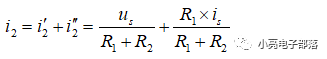
6、戴维南定理
(1)一个含独立电源,线性电阻和受控源的一端口,对外电路来说,可以用一个电压源和一个等效电阻的串联组合等效置换,此电压源的激励电压等于一端口的开路电压,电阻等于一端口内部全部独立源置零后的输入电阻。
(2)例题分析
已知图示电路中两个电压源均为40V,R1=4Ω,R2=R6=2Ω,R3=5Ω,R4=10Ω,R5=8Ω,求通过电阻R3的电流。
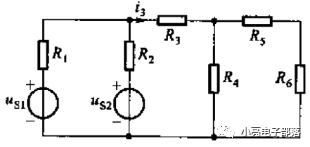
解析:将R3开路,求开路电压,而后将两个电压源置0,求开路时的等效电阻。
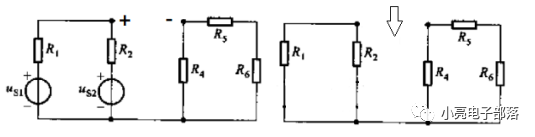
解得开路电压为40V,等效的电阻为1.33Ω,故所求的电流为3.53A。
7、诺顿定理
(1)一个含独立源,线性电阻和受控源的一端口,对外电路来说,可以用一个电流源和一个等效电阻的并联组合等效置换,此电流源的激励电流等于一端口的短路电流,电阻等于一端口内部全部独立源置零后的输入电阻。
(2)例题分析
已知图示电路中两个电压源均为40V,R1=4Ω,R2=R6=2Ω,R3=5Ω,R4=10Ω,R5=8Ω,求通过电阻R3的电流。

解析:将R3短路,求短路电流,而后将两个电压源置0,求开路时的等效电阻。
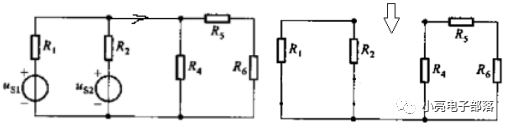
解得短路电流为6.32A,等效阻抗为6.33Ω,故所求的电流为3.53A。
二、数学应用部分
1、利用初等行变换求解线性方程组
此部分内容属于线性代数的章节,在这里阐述的目的在于如何利用简便方式计算多个未知数组成的方程。
(1)初等行变换:对线性方程组的系数矩阵或者增广矩阵做初等行变换就可以非常简便的求出线性方程组的解,计算的原理不需要读者进行研究,只需要记住结论应用即可。矩阵的初等变换主要分为倍乘与线性叠加两类。注意:对于方程组的求解仅允许使用初等行变换, 禁止使用列变换 (除非未知数转置)。
(2) 计算步骤 :写出系数矩阵(对于齐次线性方程组)或增广矩阵(对于非齐次方程组)→对矩阵进行初等行变换变为行阶梯型矩阵或最简行阶梯型矩阵→根据阶梯矩阵直接写出未知数的解即可。
2、例题分析
(1)求齐次线性方程组的解。
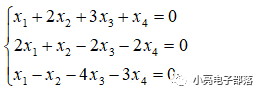
解:写出系数矩阵
第一步:第一行的-1倍加到第三行,第一行的-2倍加到第二行;
第二步:第二行的-1倍加到第三行;
第三步:第三行的8倍加到第二行,第三行的-3倍加到第一行;
第四步:第二行直接乘-1/3;
第五步:第二行的-2倍加到第一行。
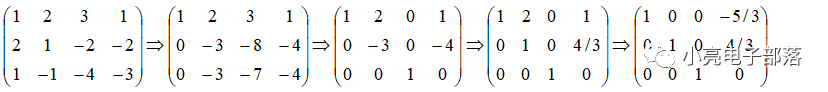

(2)求解下列非齐次线性方程组
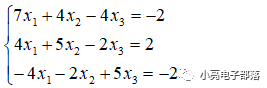
解:写出系数矩阵
第一步:第二行的1倍加到第三行,第二行的-1倍加到第一行;
第二步:第一行的-1倍加到第二行;
第三步:调换第一行与第二行的位置,第三行直接乘以1/3;
第四步:调换第三行与第二行的位置,并把第一行的-3倍加到第三行;
第五步:第二行的19倍加到第三行;
第六步:第二行的-6倍加到第一行,第三行直接乘以1/17;
第七步:第三行的-1倍加到第二行,第三行的6倍加到第一行。
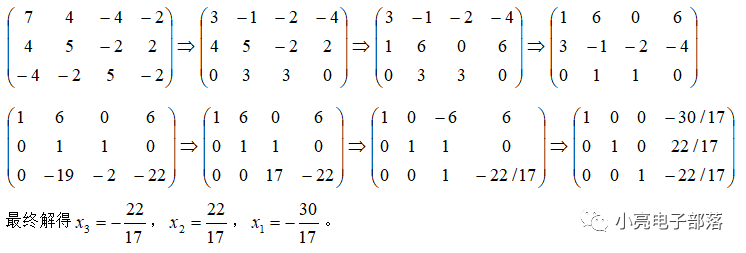
-
高效电路分析:叠加定理、支路分析法、网孔分析法、结点分析法、戴维南和诺顿定理2023-03-13 8973
-
线性电路的基本定理2023-03-09 9319
-
电路分析定理2022-06-26 574
-
电路分析的基本方法及定理PPT下载2021-08-26 885
-
在分析电路时常用的定理有哪些2021-03-11 1490
-
计算噪声对电路影响的定理分析2020-09-04 6615
-
诺顿定理的等效电路说明2019-06-23 46929
-
考研电路必备资料电路考研大串讲PDF电子书免费下载2019-04-19 10490
-
电路的基本概念和基本定理2017-07-03 2632
-
电路设计--电路定理2017-02-28 927
-
求电路定理分析习题2013-01-28 2503
-
电路定理教案(PPT讲稿)2009-07-08 368
-
电路定理2008-12-04 1211
全部0条评论

快来发表一下你的评论吧 !

