

拉普拉斯变换在电路中的应用
描述
1、拉普拉斯变换
(1)之前的一阶电路和二阶电路的分析,所应用的方法是根据电路定理和元件的电压,电流关系建立线性常微分方程,通过求解微分方程的解求得电路的时域响应,这种方法又称为经典法。但是对于多个动态元件的复杂电路(一般指同时存在R,L,C的电路),直接求解微分方程比较麻烦,例如对于一个n阶方程,直接求解时需要知道变量及其二阶导数在t=0时刻的初值,但是这些值求解起来非常麻烦。所以对于高阶系统,一般采用积分变换法,将时域函数变为频域函数,从而将时域微分方程转为频域代数方程求解,求出频域解后在还原为时域解。拉普拉斯变换是一种重要的积分变换。

2、拉普拉斯变换的性质


3、典型信号的拉普拉斯变换
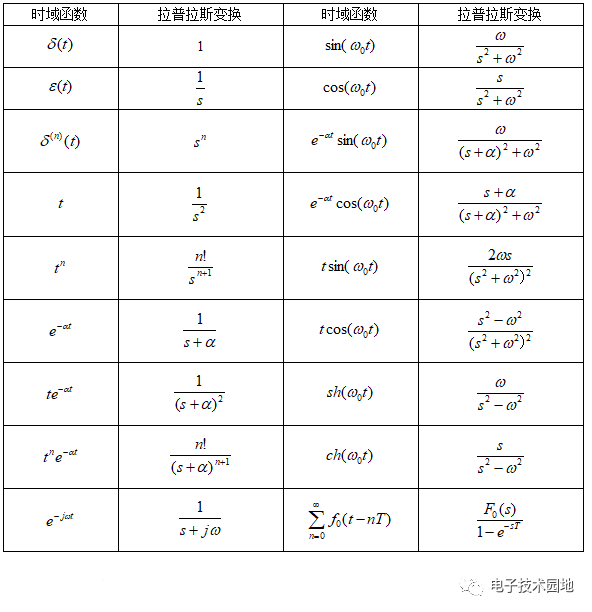
(1)拉普拉斯变换和傅里叶变换一样,都应尽量避免积分运算,利用性质和基本信号的公式来求解。
(2)关于周期信号的拉氏变换有

4、拉普拉斯变换在电路中的应用
(1)利用拉普拉斯变换来分析电路的参数过程如下:
第一步:将输入激励进行拉氏变换;
第二步:将电路中的R,L,C元件的拉氏变换形式写出来,列写所求的变量与激励之间的关系;
第三步:反解复频域形式的变量;
第四步:将复频域形式的变量做拉氏反变换。
(2)元件的时域与复频域形式的电压电流关系(电压电流均取关联参考方向)
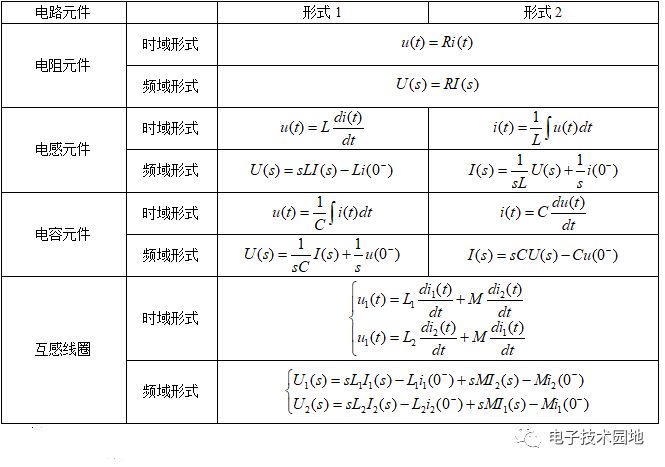
5、例题分析
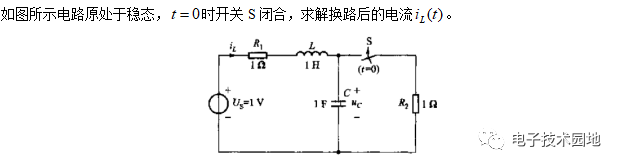

声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
拉普拉斯变换的意义2023-09-07 6524
-
拉普拉斯变换表下载2021-12-30 1007
-
拉普拉斯变换在现代控制领域有哪些应用?2021-04-29 2660
-
计算机Fortran编程实现偏微分方程拉普拉斯变换2020-08-14 3418
-
拉普拉斯变换及其逆变换表拉普拉斯变换及其逆变换表2017-12-05 266039
-
拉普拉斯变换及其应用_elecfans.com2015-10-28 1293
-
应用拉普拉斯变换分析RLC电路2010-04-12 4891
-
拉普拉斯变换2009-07-27 6124
-
拉普拉斯变换课件教案2009-07-09 681
-
什么是拉普拉斯变换2009-07-08 7456
全部0条评论

快来发表一下你的评论吧 !

