Z变换在电路中的应用

1、Z变换

（1）Z变换主要用于分析离散系统的输出响应。对于离散信号，通常采用计算机采样的方式将模拟信号进行采样来得到，17世纪发展起来的经典数值分析技术奠定了这方面的数学基础。对于连续系统，通常采用微分方程来描述系统的输入和输出。对于离散系统，通常采用差分方程来描述系统，但是计算差分方程与计算微分方程一样，对于差分方程的变量初值只能通过迭代计算来获取，所以采用Z变换的方式将差分方程变为Z域的代数方程进行计算。通过解得代数方程的解来获取Z域的响应形式。而后采用逆Z变换解得时域的系统输出响应。

（2）离散系统有三个环节：倍乘，延迟和累加。

（4）由级数的和的性质可知，级数必须收敛时，z变换才有意义，这个级数的收敛域称为z变换的收敛域，对于z变换来说，做z变换时，必须标上收敛域。

2、Z变换的性质

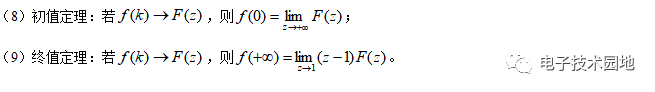
3、典型信号的Z变换

除上述表格所列出的Z变换之外，还有两个比较复杂的Z变换。

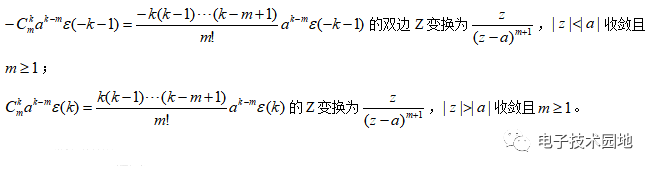
Z变换和之前两个变换一样，因为幂级数求和有时候比积分求和还要麻烦，所以应尽量避免求和运算，利用性质和基本信号的公式来求解。

4、Z变换在系统中的应用

第一步：根据系统框图列写差分方程；

第二步：将差分方程两端进行z变换；

第三步：反解z域形式的解；

第四步：将z域的解做逆z变换。

6、例题分析