二端口矩阵与系统函数

引言

这一部分的内容是之前12部分内容的综合，也是电路分析基础部分的最后一章内容。是利用之前所学的全部内容对系统和电路进行的深层理解。

1、二端口网络参数矩阵

（1）之前讨论的电路主要是在一个电路及其输入给定的情况下，如何去计算一条活着多条支路的电压和电流，若一个复杂的电路只有两个端子向外连接，且仅对外接电路中的情况感兴趣，则该电路可以视为一个一端口。在工程中遇到的问题经常涉及两对端子之间的关系，比如变压器，滤波器，放大器等等。如果两对端子满足端口条件，即对于所有时间t，从端子1流入方框的电流等于从端子1’流出的电流，同时，从端子2流入方框的电流等于从端子2’流出的电流，这种电路称为二端口网络（简称二端口）。

（2）二端口矩阵分为Z参数矩阵（阻抗矩阵），Y参数矩阵（导纳矩阵），T参数矩阵（A参数矩阵），H参数矩阵四种，下面给出推导步骤：

假定存在一个二端口结构如下图所示

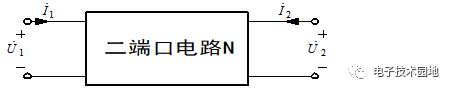
（4）二端口的连接：二端口的连接方式有三种，即级联方式，并联方式和串联方式，如下图所示：

2、系统框图

在系统设计的时候，需要首先进行框架设计，即先构思出系统的各个模块（即实现某个功能的部分），而后将模块组合，连续系统中，系统具有数乘器，加法器，乘法器，微分器和积分器。而离散系统中，系统具有加法器，数乘器和单位延迟器，系统框图如表所示。

3、信号流图

系统框图绘制比较麻烦，所以，为了简便的绘制系统框图通常采用信号流图的方式，在连续系统中，系统一般有数乘器，加法器，微分器和积分器。而离散系统中，系统则具有加法器，数乘器和单位延迟器，各部件的信号流图如下表所示。

5、系统稳定性判定

（1）通常称令系统函数的分母为0的点成为极点，分子为0的点称为零点。

（2）对于连续系统的稳定性，当系统函数的极点均位于s域左半平面的时候，系统才稳定，否则就不稳定，通常对于高阶多项式通常采用R-H准则判断系统的稳定性，但是如果可以求解出系统函数的极点，也可以不使用用这种方式。

（3）对于离散系统的稳定性，若系统为因果系统，当系统函数的极点均位于单位圆内时，系统稳定。当无法使用极点来判断的时候，通常采用朱里阵列来判断离散系统是否稳定。

注：由于朱里阵列和R-H准则太过复杂，所以请读者自行百度即可。

6、系统的输出方程的矩阵形式与状态方程的矩阵形式

通过列写状态变量与输入和输出之间的关系来确定状态方程，其实就是利用输入与输出来描述状态变量，用状态变量来描述系统的输出。采用例题的方式进行解释。

7、例题分析

（1）例题1：求图示电路的Z参数，Y参数和T参数矩阵。

（2）例题2：求解信号流图所表示的系统函数（未标出的之路增益为1），写出图2的状态方程与输出方程的矩阵形式，并判断图2所示系统的稳定性。