

数学工具在电路分析中的应用
描述
1、线性方程组的求解
(1)矩阵的初等行变换:矩阵的初等行变换有三种变换,即交换两行,以数k乘某行所有元素,将某一行的k倍加到另一行。例如将如下矩阵进行行变换有:
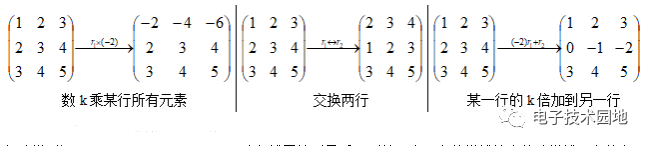
(2)行阶梯型矩阵与行最简形矩阵
行阶梯型矩阵是:从第一行某元素左方的竖线开始到最后一列某元素下方的横线结束的阶梯线,它的左下方的元素全为0;每段竖线的高度为一行,竖线的右方的第一个元素非零,如图所示:
行最简形矩阵是:若行阶梯型矩阵非零行的首个非零元素为1,且非零元素所在的列其他元素均为0,如图所示:
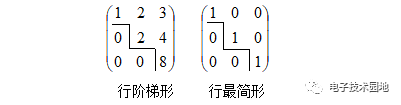
(3)求解齐次线性方程组的步骤是:将方程组的系数写成矩阵形式,然后采用初等行变换将矩阵化为行阶梯型矩阵或行最简形矩阵。
(4)方程组的解具有三种可能:有唯一解,有无穷多解和无解。
齐次线性方程组不可能无解,最次也有0解,故齐次线性方程组只有两种情况:若系数矩阵存在全0行,则方程组有无穷多解,若不存在全0行,则方程组有唯一解。
非齐次线性方程组由于增加了一列方程中等号后面的元素,所以有三种情况,若系数矩阵存在全0行,则方程组有无穷多解,若系数全为0且等号后面的数也为0,则方程组有唯一解,若系数全为0但等号后面的数不为0,则方程组无解。
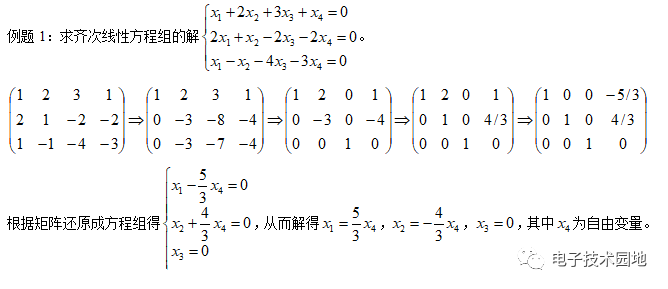

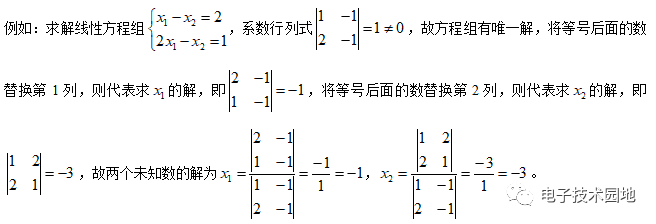
(5)克拉默法则:建议克拉默法则最好只用在有2个未知数的方程组。
写出系数行列式,若系数行列式不为0,则方程组有唯一解,反之,放弃克拉默法则。
2、多项式合并为乘积的形式
(1)二次多项式的合并:对于二次多项式,一般可以凑完全平方公式或者采用因式分解的方式变为乘积的形式,如
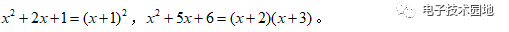
(2)三阶以上多项式的合并
方法1:采用杨辉三角可以根据系数看出乘积的形式,杨辉三角的排列如下图所示:
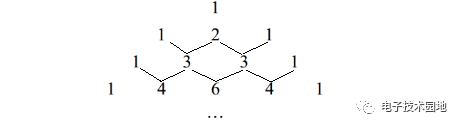
方法2:多项式除法,无论是阶次多高的方程,只要能看出一个使等式为0的解,即可采用多项式除法。

方法3:利用恒等的原则,将奇次项与偶此项划分在等式两边进行合并同类项。
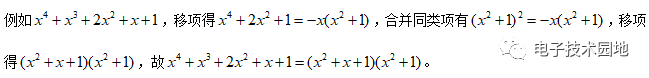
3、 乘积形式化为代数和形式 (有理函数拆分)
对于有理函数的拆分,首先将分母写为乘积的形式,而后采用如下两种方法之一即可。分母写为乘积形式有两种情况需要注意:

4、此外,函数的求导,积分,级数求和在电路分析中也经常用到,这三部分内容请参照高等数学学习即可。
-
数学分析原理rudin著下载2008-09-26 8989
-
Matlab符号数学工具箱应用说明2009-09-22 4365
-
matlab数学建模工具箱2011-07-10 24278
-
数学分析2017-01-10 4945
-
漫谈电路、信号处理中的“虚部”2017-10-25 2945
-
什么是射频/微波设计用电磁和数学软件?2019-07-30 1136
-
如何使用工具链中自带的数学函数呢2022-09-26 3199
-
数学建模与数学实验-回归分析2008-12-03 755
-
小学数学命题分析2009-01-09 1105
-
《高等数学》知识在物理学中的应用举例2010-05-15 1358
-
一种用于形状精确描述的数学工具2017-12-25 859
-
2023版《90天模拟电路分析方法与数学基础》线上特训营,限时优惠!2023-03-11 2100
-
氧气传感器在化学工业中的应用2023-06-16 1083
-
傅里叶变换的数学意义2023-09-07 1838
-
神经网络在数学建模中的应用2024-07-02 2302
全部0条评论

快来发表一下你的评论吧 !

