什么是编译器算法之寄存器分配
描述
0.前言
寄存器是CPU中的稀有资源，如何高效的分配这一资源是一个至关重要的问题。本文介绍了基于图着色的寄存器分配算法。
寄存器分配看似离我们很遥远，实际上在我们的生活中就有类似的问题，例如为每个班级分配上课的教室就与寄存器分配有着相似性。
其中班级相当于程序中的变量，教室相当于寄存器。在同一个时间段上课的两个班级不能分配到一个教室，对应于寄存器分配就是两个同时活跃的变量不能分配同一个寄存器。
可见寄存器分配是一个非常有趣且值得研究的问题。
1. 为何进行寄存器分配
Fig 1.1 内存层次图
从上面的Fig 1.1的图中可以看到，计算机系统的内存共分为四个层次：寄存器、 缓存、内存、硬盘。
实际上数据在这四种形式的内存中的移动由三个对象负责管理，这三个对象分别是应用程序、硬件、编译器。
- 应用程序只负责管理数据在内存和硬盘之间的移动，其它形式的内存对应用程序而言是透明的。
- 硬件负责管理数据在内存和缓存之间的移动。
- 编译器负责管理数据在寄存器和内存之间的移动。
而CPU的运算速度远高于内存的存取速度，其中寄存器与CPU的通信速度最快，所以合理的利用寄存器，能够提高程序的效率。这也是为啥寄存器分配在编译器中属于非常重要的一部分。
2 算法总架构
整个算法分为多个步骤，每个步骤相对来说较为复杂，对于每一步会单独分一个小节介绍。在单独介绍每一步之前，先来看一下寄存器分配的总流程图
Fig 2.1 寄存器分配流程图
- Make_Webs()函数
多个相交的du链形成一个网，Make_Webs函数用来发现du链中所有的网。
- Build_AdjMtx()函数
冲突图需要用一个二维的邻接矩阵表示，该邻接矩阵的下三角表示两个寄存器是否冲突。AdjMtx[i,j] = true表示符号寄存器(或真实寄存器)i与j相互冲突。
- Coalesce_Regs()函数
使用邻接矩阵合并寄存器。会搜索赋值指令例如 Si = Sj这样的指令，而且要满足Si与Sj不相互冲突（AdjMtx[i,j]的值为false）。如果找到这样的指令，就会将对Sj的定义改为对Si的定义，并删除改赋值指令。如果执行了寄存器合并，则跳转到1继续执行，如果没有则进行下一步
- Build_AdjLsts()函数
构建一个邻接表，其中的每一个元素表示一个符号寄存器，记录了与符号寄存器相关的信息。邻接表用一个数组AdjLsts[1..nwebs]表示，数组中的每一个元素是一个listrecd记录。
- Compute_Spill_Cost函数
计算每个符号寄存器溢出到内存和从内存恢复到寄存器的开销。
- Prune_Graph()
使用degree
- Assign_Regs()
根据邻接表的信息给每个节点着色，不相邻的两个节点可以有相同的颜色。如果成功则执行Modify_Code()将符号寄存器换为真实寄存器。如果着色失败，则执行下一步
- Gen_Spill_Code
将符号寄存器溢出到内存，产生相应的store/load指令。如果重建该值的开销小于溢出，也可重新计算该值，而不是溢出到内存。然后返回到步骤1
- Modify_Code
如果步骤7成功，则执行Modify_Code,将分配的颜色替换为实际的寄存器。
算法的伪代码如下：
do
do
Make_Webs();
Build_AdjLsts();
C = Coalesce_Regs();
while !C
Build_AdjLsts();
Compute_Spill_Costs();
Prune_Graph();
Succ = Assign_Regs();
if Succ
Modify_Code();
else
Gen_Spill_Code();
while Succ
接下来的每一小节是对每个步骤的具体介绍。
3.构建web
网是寄存器分配的对象。使用网而不是变量做为寄存器分配的对象是因为同样的变量名可能在程序重复使用，但这些同名变量却毫不相关。
例如一个程序中会多次使用i做为多个for循环中的循环变量，但这些for循环其实是不相关的。
网的定义：多条相交的du链属于同一个网，即多个du链有一个共同的use。
具体的web例子如下：
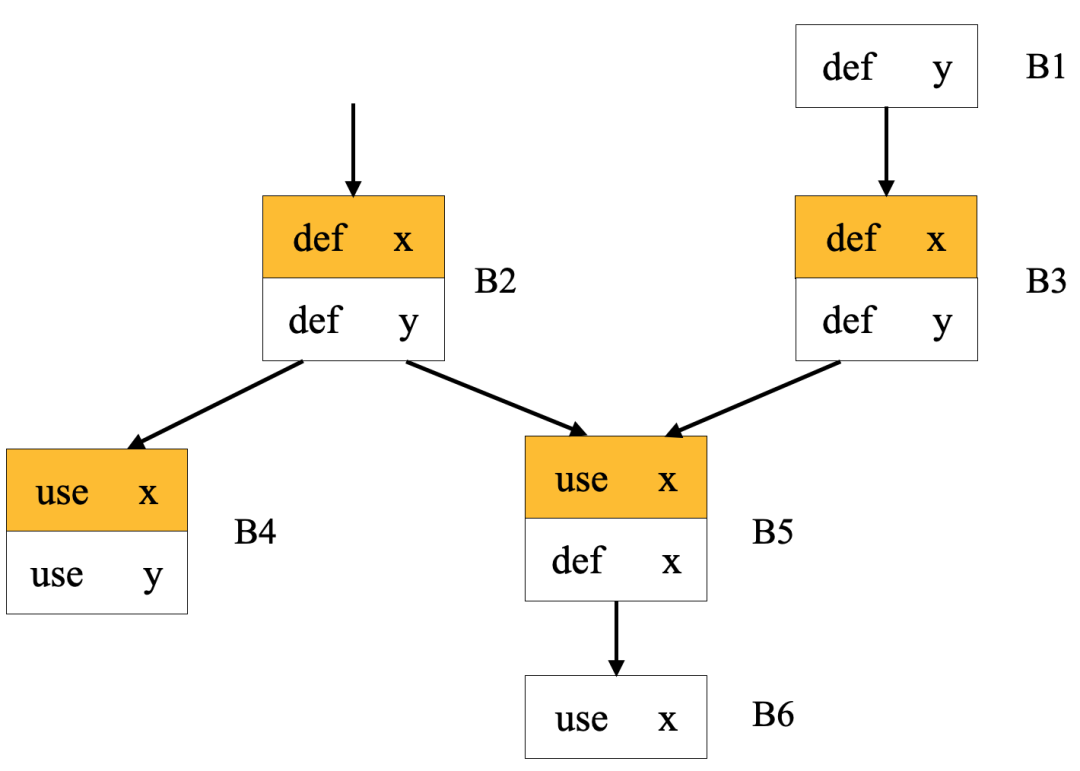
Fig 3.1 多个web构成的一个webs
图中的黄色部分是最复杂的一个网（下表中的W1)，即两条du链有共同的use，因此这两条du链构成一个网。
图中共有四个网，具体如下表
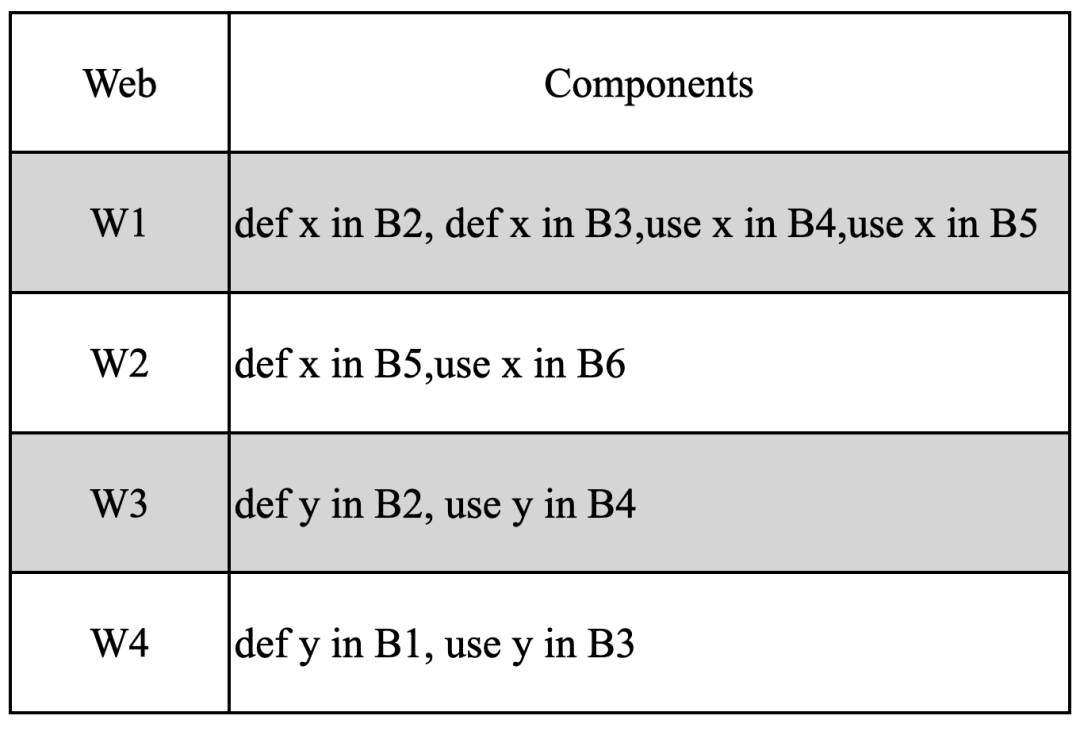
Fig 3.2 来自Fig 3.1的网
du链在算法中的类型为UdDuChain，由一个三元组组成，s表示一个符号，p表示s所表示的符号的def所在的位置，Q表示该符号use的集合。
可以通过下面的例子来熟悉du链在算法中的表示
黄色部分第一条du链用如下符号表示：
<<x,
即x在B2中的第一条指令处定义，在B4和B5中的第一条指令处都有使用。
黄色部分第二条du链
<<x,
两条du链在中有共同的use，因此两条链最终构成一个网：
{
<<x,
如果用sdu表示类型为UdDuChain的一条du链，则sdu@1表示符号s，sdu@2表示def所在的位置p，sdu@3表示use集合Q
<<x,
对于上图的du链，sdu@1表示x，sdu@2表示def 。
sdu@3表示use集合{,}即x在和处都有使用。
弄清楚了每个符号的含义，看懂下面的算法实现就容易了。
首先是webs的初始化，将每个du链视为一个web。
//用du链初始化web
for each sdu in DuChains{
nwebs += 1;
webs U= {
需要注意的是，U= 表示求并集，代码中symb:sdu@1表示将sdu@1赋值给symb。
然后是将有共同use的du链合并到一起形成web。
do{
oldnwebs = nwebs;
TmpWebs1 = Webs;
while(TmpWebs1 != null){
// #号表示从TmpWebs1中取出一个web
web1 = #TmpWebs1;
TmpWebs1 -= {web1};
TmpWebs2 = TmpWebs1;
while(TmpWebs2 != null){
web2 = #TmpWebs2;
TmpWebs2 -= {web2};
if( web1.symb = web2.symb &&
( web1.uses - web2.uses) != null)
{
web1.defs U= web2.defs;
web1.uses U= web2.uses;
webs -= {web2};
nwebs -= 1;
}
}
}
}while(oldnwebs!=nwebs)
一句话概括算法主要思想：在TmpWebs1中取其中一个网记作web1，除去web1后剩下的网组成TmpWebs2，并在TmpWebs2中取一个网记作web2，如果web1与web2有共同的use，则合并web1与web2，直到TmpWeb1s为空为止。
最后是将webs中的每一个web和真实寄存器放到同一个数据结构SymReg[i]中
// 1到nregs为真实寄存器
for( i = 1 to nregs){
Symreg[i] = {
4. 构建冲突图
冲突图在算法中用邻接矩阵和邻接表这两种数据结构来表示。
邻接矩阵用来表示两个节点之间是否相互冲突，而邻接表用来表示每个节点的一些其他信息。
以如下代码为例构建冲突图：
s1 = 2;//row 1
s2 = 4;//row 2
s3 = s1 + s2;//row 3
s4 = s1 + 1;//row 4
s5 = s1*s2;//row 5
s6 = s4*2//row 6
假定有三个寄存器r1，r2，r3可用，且s4不能存储在r1中。
上述程序的冲突图如下：
Fig 4.1 冲突图
图中的边表示两个符号寄存器存在冲突，即两个符号寄存器不能分配到同一个真实寄存器中。s4与r1的边表示s4不能分配到r1。
本节中邻接表和邻接矩阵的建立都是以上面的这个冲突图为例。
4.1 建立邻接矩阵
Fig 4.2 邻接矩阵表示冲突图
图Fig 4.2是用矩阵表示图Fig 4.1中的冲突图。true表示两个节点相互冲突，false表示两个节点没有冲突。
邻接矩阵在算法中用一个二维数组AdjMtx[i,j]表示。AdjMtx的初始化代码如下：
//注意i从2开始取是因为Fig 4.2中的行是从r2开始
for i =2 to nwebs{
for j = 1 to i-1{
//下三角全部初始化为false
AdjMtx[i,j] = false;
}
}
//任何两个真实寄存器之间相互冲突
for i = 2 to nregs{
for j = 1 to i-1{
AdjMtx[i,j] = true;
}
}
初始化后对于两个冲突的节点i与j对应的AdjMtx[i,j]需要置为true。具体算法如下。
函数Interfere用来判断符号寄存器与真实寄存器是否存在冲突。函数Live_At用来判断两个符号寄存器之间是否冲突。
for i = nregs to nwebs{
for j = 1 to nregs{
if Interfere(Symreg[i],j){
AdjMtx[i,j] = true;
}
}
for j = nregs+1 to i-1{
for each def in Symreg[i].defs{
if Live_At(Symreg[j],Symreg[i].symb,def){
AdjMtx[i,j] = true;
}
}
}
}
4.2 建立邻接表
除了邻接矩阵之外还需要用邻接表记录邻接矩阵中每个元素的一些相关信息。邻接表中的每个元素也代表了每个寄存器的信息，包括真实寄存器和符号寄存器。
邻接表用一个数组表示，数组的每个元素是一个结构体，共六个字段，分别是color, disp, spcost,nints, adjnds, rmvadj。
- color表示该节点的颜色
- disp表示该符号寄存器溢出到内存的地址
- nints表示与该节点相互冲突节点的个数
- adjnds是一个链表，保存了与当前节点相互冲突的所有节点
- rmadj也是一个链表，保存了移除的部分节点，这些移除的节点也是与当前节点相冲突的
下图是用来表示Fig 4.1中冲突图的一个邻接表。
Fig 4.3 表示Fig 4.1的初始化邻接矩阵
邻接表的初始化代码如下：
for i = 1 to nregs{
AdjLsts[i].nists = 0;
AdjLsts[i].color = -Max;
AdjLsts[i].disp = -Max;//-Max表示负无穷
AdjLsts[i].spcost = Max;//Max表示正无穷
AdjLsts[i].adjnds = null;
AdjLsts[i].rmvadj = null;
}
for i = nregs + 1 to nwebs{
AdjLsts[i].nists = 0;
AdjLsts[i].color = -Max;
AdjLsts[i].disp = -Max;
AdjLsts[i].spcost = 0.0;
AdjLsts[i].adjnds = null;
AdjLsts[i].rmvadj = null;
}
for i = 2 to nwebs{
for j = 1 to i-1{
if AdjMtx[i,j]{
AdjLsts[i].nists += 1;
AdjLsts[i].adjnds += [j]
AdjLsts[j].nists += 1;
AdjLsts[j].adjnds += [i]
}
}
}
5.寄存器合并
对于赋值指令来说，实际上应该把两个寄存器当做一个来处理，这实际上也是复写传播的一个变种。
Sj = Si//类似于这种只有两个寄存器的赋值指令
当两个寄存器出现在赋值指令的两端而且两个寄存器不存在相互冲突，并且两个寄存器在赋值指令到程序结束没有被赋值，可以将这两个寄存器在相互合并(合并邻接表和邻接矩阵)。
具体操作分四步：
- 查找Sj = Si 这样的赋值指令，满足Si与Sj互不冲突，且Si与Sj到程序结束没有赋值，如果找到则进行下面步骤
- 寻找向Si赋值的指令，将Si改为Sj
- 移除赋值指令Sj = Si
- 调整邻接矩阵表示的冲突图，以及合并Si与Sj所在的网。
for i = 1 to nblocks{
for j =1 to ninsts[i]{
if LBlock[i][j].kind = regval
//获取Si = Sj 指令的左边的寄存器号Si
k = Reg_to_Int(LBlock[i][j].left);
//获取Si = Sj 指令的右边的寄存器号Sj
l = Reg_to_Int(LBloclk[i][j].opd.val);
//步骤1
if !AdjMtx[max(k,l),min(k,l)] && Non_Store(LBlock,k,l,i,j)
{
for p = 1 to nblocks{
for 1 =1 to ninsts[p]{
if LIR_Has_Left(LBlock[p][q])&&
LBlock[p][q] == LBlock[i][j]
{
//步骤2
LBlock[p][q].left = LBlock[i][j].left
}
}
}
//步骤3
delete_inst(i,j,ninsts,LBlock,Succ,Pred);
//步骤4
Symreg[k].defs U= Symreg[l].defs;
Symreg[k].uses U= Symreg[l].uses;
//调整邻接矩阵,直接将最后面的节点覆盖掉合并后不需要的l节点。
Symreg[l] = Symreg[nwebs];
for p = 1 to nwebs{
if AdjMtx[max(p,l),min(p,l)]
AdjMtx[max(p,k),min(p,k)] = true;
else
AdjMtx[max(p,l),min(p,l)] = AdjMtx[nwebs,p]
}
nweb -= 1;//合并后web的数量减1
}
}
}
需要注意的是代码中AdjMtx[max(k,l),min(k,l)]中的 max(k,l)出现在矩阵的下标是因为我们是用下三角来表示冲突图的，而且行号要比列号大，具体参照Fig 4.2表示的邻接矩阵就明白了。
6. 计算溢出开销
将符号寄存器的值溢出到内存的目的是为了让所有的变量都有地方保存，当寄存器的数量不够时，就需要将符号寄存器的值溢出到内存。
将符号寄存器的值溢出到内存，可以减少冲突图中某个节点与其它节点冲突的数量，从而使整个冲突图可以R着色。
溢出的开销通常用一个公式来计算，这个公式也是启发式的，通常使用如下公式。
其中def、use、copy分别是网w中的各个定值、使用和寄存器复制，defwt、usewt、copywt是对应的权重。
具体代码如下：
//Compute_Spill_Costs函数的具体实现
for i = 1 to nblocks
{
for j = 1 to ninsts[i]
{
inst = LBlock[i][j]
switch(LIR_Exp_Kind(inst.kind))
{
//二元表达式
case binexp:
//操作数1的类型是寄存器编号
if inst.opd1.kind == regno
//depth(i)表示循环的层数
AdjLsts[inst.opd1.val].spcost] += UseWt*10^depth(i);
if inst.opd2.kind == regno
AdjLsts[inst.opd1.val].spcost] += UseWt*10^depth(i);
break;
//一元表达式
case unexp:
if inst.opd.kind == regno
if inst.kind == regval
AdjLsts[inst.opd.val].spcost -= CopyWt*10^depth(i);
else
AdjLsts[inst.opd.val].spcost += UseWt*10^depth(i);
break;
case noexp:
break;
}
//指令有左值且指令的类型为复写指令
if LIR_Has_Left(inst.kind) && inst.kind != regval
AdjLsts[inst.left].spcost += DefWt*10^depth(i);
}
for i = nregs + 1
{
//r表示重新计算该值的开销
r = Rematerialize(i,nblocks,ninsts,LBlock)
if r < AdjLsts[i].spcost
AdjLsts[i].spcost = r;
}
}
7. 修剪冲突图
度
假设没有这个度小于R的节点时该冲突图是R着色的，因为这个节点的度小于R，故至少有一种颜色没有被与它相邻的颜色使用，因此这个颜色可以分配给这个度小于R的节点。
因此我们的做法就是：重复的寻找图中那些相邻的节点数小于R的节点，每当找到一个这样的节点，便将它从图中删除，并放到栈中，以便按照逆序对节着色。
在这个处理过程中每一个删除节点会记录到与之相邻节点的rmvadj域值。
如果最后能够删除此图中的所有节点，就能够确定该图是可以R着色的。然后从栈中弹出这些节点，并给每一个节点赋予一个颜色。
但是图中可能会存在度大于R的节点，在这种情况下，我们应该保持一种乐观的启发式，即选择一个度大于R且具有最小溢出代价的节点，并乐观的将该节点压入栈中，我们这样做的是期望将来它的邻接点不会用完所有的颜色，因此将应在修剪冲突图时做出的决定推迟到实际给节点指派颜色时。
//Prune_Graph函数
do
{
//根据度
8.着色
//Assign_Regs函数
do
{
r = stack.pop();
//返回没有给r的冲突节点着色的最小颜色
c = Min_Color(r);
if c > 0
{
if r <= nregs
{
Real_Reg(c) = r;
}
}
else
{
//如果无节点可用，标记该节点溢出
AdjLsts[r].spill = true;
success = false;
}
}while Stack == []
如果上面的寄存器分配成功则直接修改指令，将符号寄存器修改为真实寄存器。否则要产生溢出符号寄存器相关的指令。
9. 溢出符号寄存器
如果寄存器分配不成功，需要将寄存器溢出到内存中，然后进行寄存器分配。具体的代码如下：
//Gen_Spill_Code
for i = 1 to nblocks
{
for j = 1 to ninsts[i]
{
inst = LBlock[i][j];
switch( LIR_Exp_Kind(inst.kind) )
{
case binexp:
//如果二元表达式的opreand1需要spill
if AdjLsts[inst.opd1.val].spill
{
//获取inst.opd1.val溢出到内存地址
Comp_Disp(inst.opd1.val);
//在当前使用opd1的指令之前插入load inst.opd1.val的指令
insert_before(i,j,ninsts,LBlock,
10. 后记
算法主要来自于鲸书（Advanced Compiler Design Implementation）。本文是鲸书的一个笔记，对里面的代码进行了微小的调整，也加入了详细的注释，方便大家理解。
-
线性汇编-寄存器分配疑问 请问为什么不同的变量分配了相同的寄存器？2018-08-07 0
-
编译器优化那些事儿（5）：寄存器分配2022-08-24 0
-
编译器优化的静态调度介绍2023-03-17 0
-
寄存器应用举例2009-05-17 1593
-
寄存器,寄存器是什么意思2010-03-08 21838
-
数据寄存器,数据寄存器是什么意思2010-03-08 12477
-
移位寄存器,移位寄存器是什么意思2010-03-08 17415
-
多寄存器组网络处理器上的寄存器分配技术2011-06-28 759
-
寄存器与移位寄存器2016-05-20 1134
-
MIPS寄存器详解2018-04-27 6046
-
高效的C编程之寄存器分配2017-10-17 1075
-
静态变量、自动变量与寄存器变量的存储2019-06-03 3096
-
不同思路的寄存器分配算法2022-08-24 1441
-
怎么给D寄存器输入数值 三菱plc寄存器D怎么读取2023-04-12 16436
-
寄存器分为基本寄存器和什么两种2024-07-12 1104
全部0条评论
快来发表一下你的评论吧 !
