什么是针对GPU单指令多数据流的编译优化算法

1.单指令多数据流

首先来看一段简单的if-else语句：

if(A)
{
    B = 1;//Instruction S1
    C = 2;//Instruction S2
}
else
{
    B = 3;//Instruction S3
    C = 4;//Instruction S4
}

假设代码中每条语句转换成指令后分别是S1、S2、S3、S4.

如果在CPU的单指令单数据流中，A=true时会取指令S1和S2执行，A=false时会取指令S3和S4执行，不存在A=true和A=false同时存在的这种情况。

但是在GPU的单指令多数据流（SIMD）中却存在A=true和A=false同时存在的情况。

如下图所示是GPU单指令多数据流的执行情况：

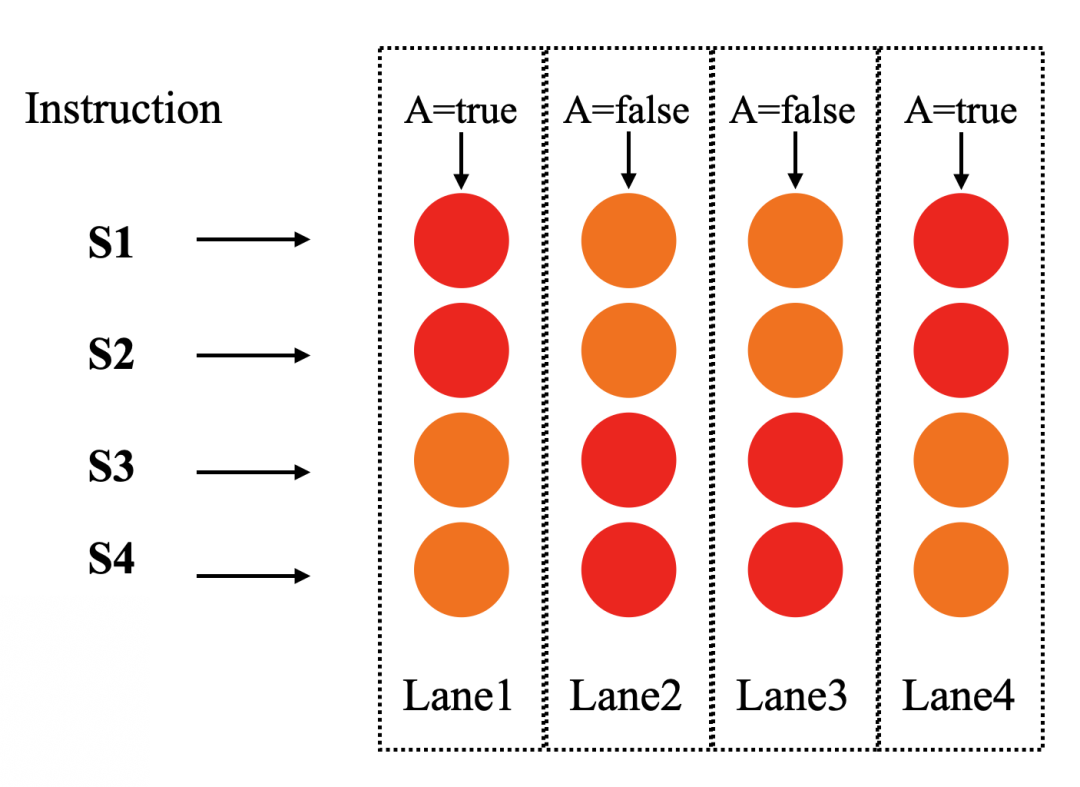
GPU单指令多数据流

从图中可以看到，GPU共有4个通道lane1、lane2、lane3、lane4，分别对应4笔不同的数据。这四个通道共享同一组指令S1、S2、S3、S4（如图中左边所示）。但是在4个不同的lane中，A的值在不同的lane中有时是true，有时是false。红色表示执行该指令，橙色表示不执行该指令。

如果按照CPU单指令单数据流的方式去编译，生成的汇编指令是大概这样的：

goto     !A , Labe1;//如果A为false，跳转
mov      B , 1;//指令S1
mov      C , 2;//指令S2
Lable1:
mov      B , 3;//指令S3
mov      C , 4;//指令S4

可以看到goto指令会根据A的值进行跳转，GPU中A的值在不同的lane中取值不同，不同的lane根据自己的A值进行跳转是行不通的。因为所有的lane共享同一组指令，不可能有的lane在执行S1、S2语句，有的lane在执行S3、S4语句。

所以GPU的指令应该转换成顺序执行，类似于下面这种。

(p0) mov      B , 1;//指令S1
(p0) mov      C , 2;//指令S2
(p1) mov      B , 3;//指令S3
(p1) mov      C , 4;//指令S4

此时不同的lane都会按照顺序取值S1，S2，S3，S4，但是具体的lane中会根据前面的p寄存器的取值确定是否执行该指令。例如对于同一条指令S1，根据A的输入，有的lane是执行的（红色），有的lane是不执行的（橙色）。

一句话总结就是：GPU是单指令多数据流（SIMD）架构，当多笔数据过来时，不一定同时跳转，本文介绍的if-conversion算法能够消除所有的跳转指令，可以将控制依赖转换为数据依赖。

2.if-conversion算法

总共分四步：

1. 计算直接后继支配节点
2. 计算控制依赖CD
3. 计算R&K函数
4. Augment K

首先要计算直接后继支配节点，因为在控制依赖CD的计算中需要用到。

什么是控制依赖CD，一个简单的例子就是if语句中的block y是受if语句所在的block x所控制的。此时CD(y) = x, 称为y控制依赖于x。

R&K分别对应寄存器p的use与def，即寄存器p的使用与定义。

R(x):表示分配给block x的谓词寄存器。block x的执行与否受R(x)中的寄存器控制。也可以说是p的use，即寄存器p用于block x。

K(p):表示谓词寄存器p需要在K(p)中的block中定义。也就是寄存器的def，即寄存器p在那个block定义。

2.1 直接后继支配节点

首先要弄清楚两个概念：后继支配节点、直接后继支配节点。

后继支配节点：如果从节点y到出口节点的每一条路径都经过节点x，则x为y的后继支配节点。

记作：x pdom y

直接后继支配节点：x pdom y，不存在节点z，使得x pdom z 且 z pdom y。则x为y的直接后继支配节点。

记作：x ipdom y

计算后继支配节点的迭代算法：

change = true;
//init pdom set
pdom(exit_block) = {exit_block}
pdom(0:eeit_block-1) = {all blocks}
//iterate flow graph
while(change)
{
  change = false;
  for( each block n) with post order
  {
    tmp = {all blocks}; 
    //求节点n所有直接后继节点的共同后继支配节点
    for(each n's successor block p)
    {
      tmp = tmp & pdom(p);//求交集
    }
    //n的后继支配节点包括他本身
    tmp = tmp | {n};
    if(tmp!=pdom(n))
    {
      pdom(n) = tmp;
      change = true;
    }
  }
}

求后继支配节点的算法一句话概括：节点n的后继支配节点包括他本身，以及他所有直接后继节点的共同后继支配节点。

计算直接后继支配节点的算法：

//remove itself from it's pdom set
for each node n
{
  pdom(n)-={n};
}

for each node n with post order
{
  for each s in pdom(n){
  //移除直接后继支配节点的后继支配节点 
    for each t in set( pdom(n)-s ){
      if( t is in pdom(s) )
        pdom(n)-={t}
    }
  }
}

后继支配节点 = 直接后继支配节点 + （直接后继支配节点）的后继支配节点

前面已经求出了后继支配节点，因此在后继支配节点中移除（直接后继支配节点）的后继支配节点，即可得到直接后继支配节点。

下图是一个计算直接后继支配节点的例子：

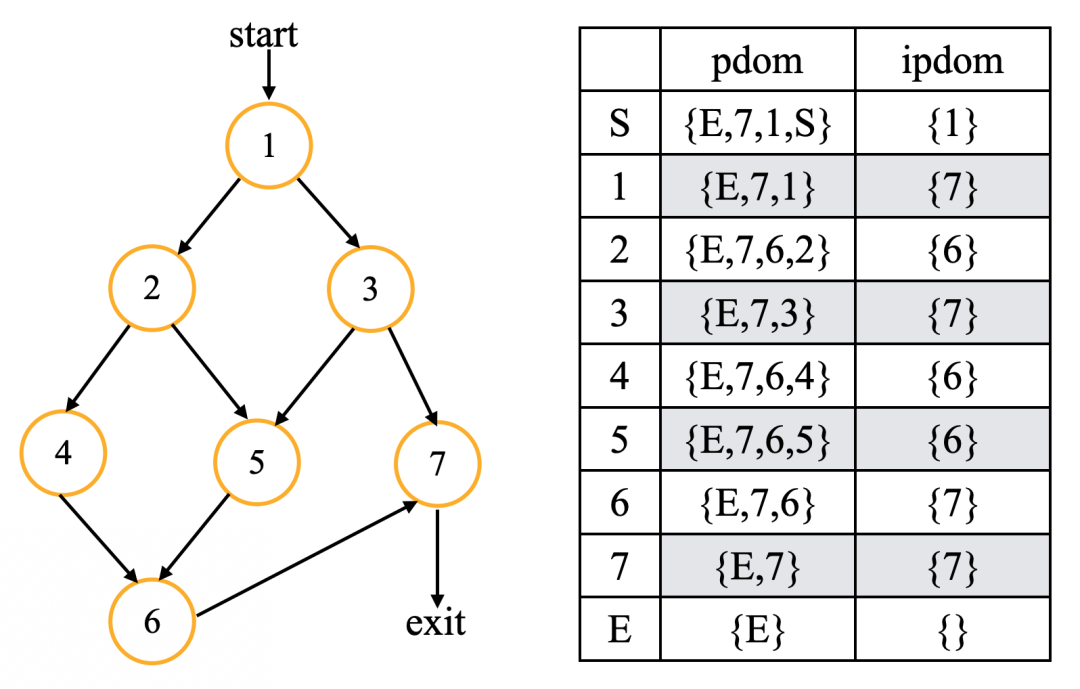
直接后继支配节点

2.2. CD

CD是Control Dependent的缩写。直接上英文定义可能更准确一些，详细证明可参考文章末尾给出的论文，公众号后台回复SIMD关键字即可下载。

Y is control dependent on X iff

(1) there exists a directed path P from X to Y with any Z in P (excluding X and Y) post-dominated by Y

(2) X is not post-dominated by Y.

计算CD的算法：

pdom(x) = {y in N: y pdom x}
ipdom(x) = {y in N: y ipdom x}

for [x,y,label] in E such that y not in pdom(x)
{
    Lub = ipdom(x);
    if !label 
      x = -x
    t = y;
    while(t!=Lub)
    {
      CD(t) = CD(t) U {x}//U表示求并集
      t = ipdom(t);
    }
}

上述伪代码中的！label表示由block x到block y的执行条件为false。

计算CD的算法用一句话概括：对于[x,y,label],在支配节点树中，从ipdom(x)到y的路径上的所有节点都控制依赖于x，不包括ipdom(x)。

以[1,2,true]为例，ipdom(x) = 7,从下面的后继支配节点树可知，7到2经过的节点有6,2（不包括7）,因此节点6和2都控制依赖于节点1.

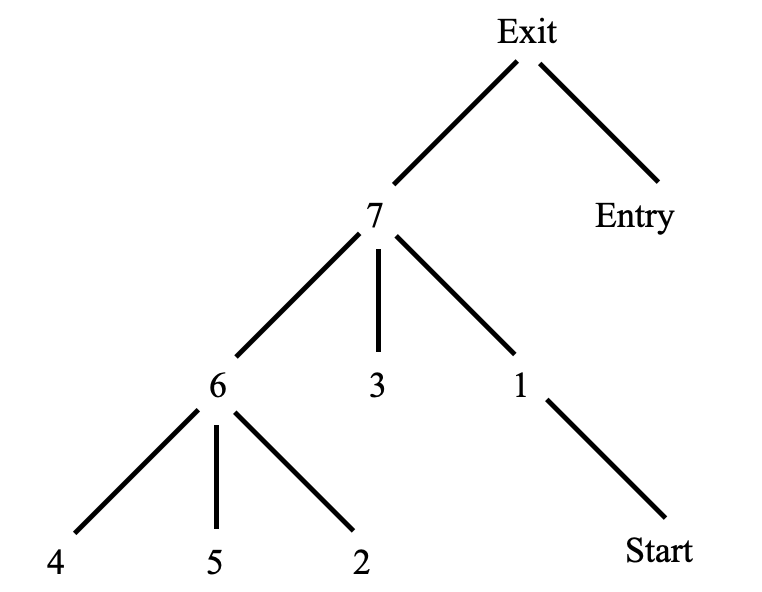
后继支配节点树

下图是CD计算的结果：整篇文章都使用同一个控制流图作为实例

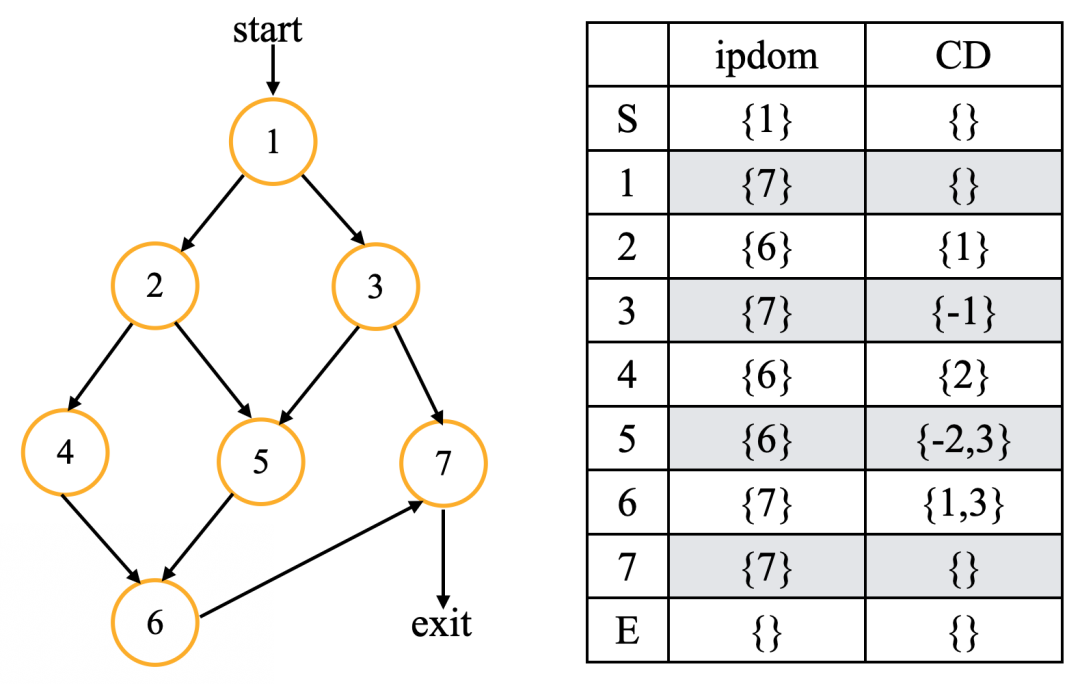
CD计算结果

2.3. 计算R&K

p = 1;
for x in N
    t = CD(x);
    if t in K
    {
        //性质2
        R(x) = q such that K(q) = t;
    }
    else
    {
        K(p) = t;
        R(x) = p++;
    }

性质1：每一个block x有且仅有一个对应的p = R(x)

性质2：对于两个不同的block，如果它们的控制依赖都为k(p),则这两个block对应的寄存器都为p（对应上述算法中的if语句）

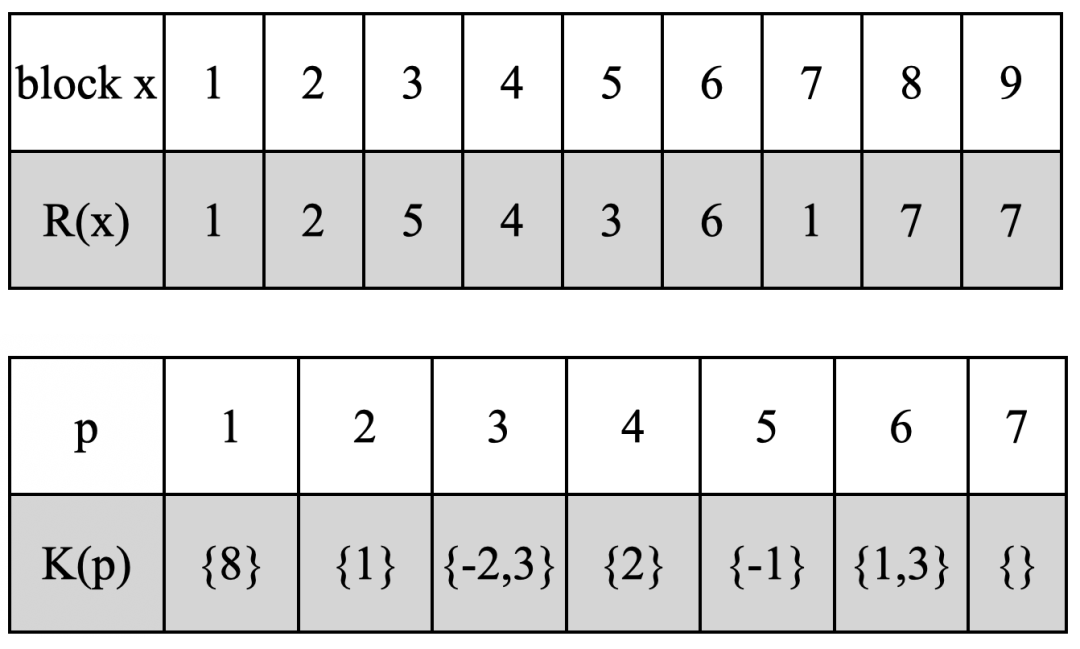
R与K的计算结果

2.4. Augment K

k(p)表明p需要在哪些block初始化，但是存在一条路径，刚好没有经过k(p),这个时候p没有被初始化。因此需要在start节点对p进行初始化。

主要是针对类似的if语句嵌套：

//原始的控制流
if(condition1)
{
    block1
    if(codition2)
    {
        block2
    }
    else
    {
        block3
    }   
}

上面的控制流最终会转化成如下的顺序执行，只是每个block会有一个p寄存器去guard。

最终会转化为这样:

//转换后的顺序执行，是否执行受p寄存器控制
（p1) block1;//p2与p3都会在block1中初始化
 (p2) block2;
 (p3) block3;

原始的控制流中p2与p3都会在block1中初始化，如果block1没有执行，那么p2与p3就没有被初始化。因此需要在开始节点处将p2与p3初始化为false。

为什么初始化为false而不是true？因为block1没有执行，说明block2与block3也不应该执行，所以初始化为false。

上述过程是为什么要做Augment K，实际上Augment K要做的只有一件事：找到未初始化的寄存器p，在start节点处将p初始化为false。

在程序中找到为初始化的变量很简单，从后向前做活跃变量分析，如果变量在入口处还是活跃的，则该变量没有被初始化。

因为从后向前做活跃变量分析的时候，变量的每次定义都会被Kill掉（公式1），如果在程序的入口处都没有被Kill掉说明该变量是没有被初始化过的。

（公式1）

（公式2）

本算法中只需要对p寄存器进行活跃变量分析，use和def分别对应已经求出的R与K。

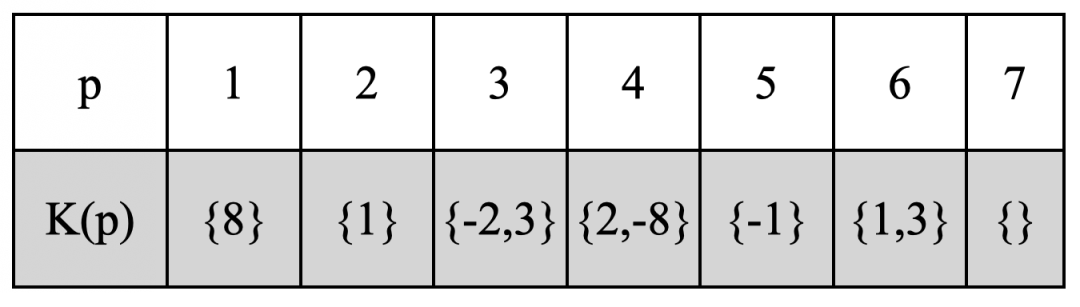
Augment K结果

四个步骤做完后最终的结果如下：

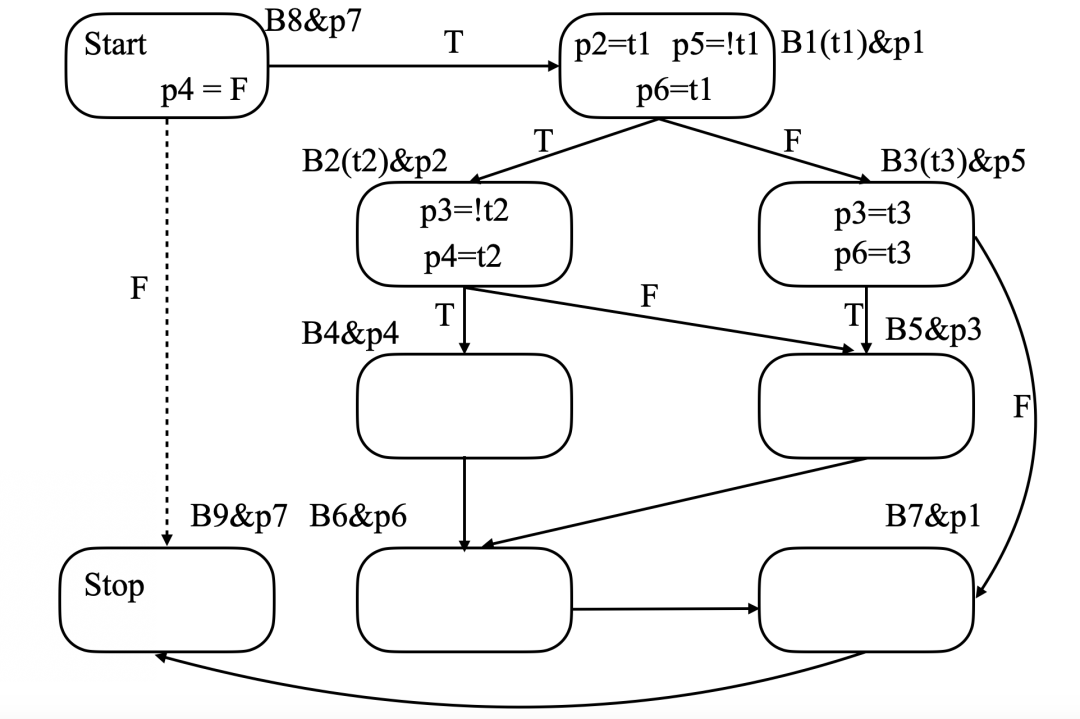
p寄存器分配的最后结果

图中B2(t2)p2表示寄存器p2控制B2，条件t2与B2相关联。

3.后记

刚接触if-conversion算法的时候觉得挺复杂的，在写文章的过程中对整个算法的理解又有了更深刻的理解，有一种无法言喻的喜悦。