光学系统的坐标系统、结构参数和光学特性参数

 

为了计算光学系统的像质评价指标，必须先明确光学系统的坐标系统、结构参数和光学特性参数的表示方法。

一．  坐标系统及常用量的符号及符合规则

坐标系与应用光学中所采用的坐标系一样。

线段从左向右为正，由下向上为正，反之为负；角度一律以锐角度量，顺时针为正，逆时针为负。

对于角度和物、像距，用大写字母代表实际量，用小写字母代表近轴量。

光学系统中常用量的符号及符号法则，如下表所示：

名称	符号	符号规则
物距	L	由球面顶点算起到光线与光轴的交点。
像距	L`	由球面顶点算起到光线与光轴的交点。
曲率半径	r	由球面顶点算起到球心。
间隔或厚度	d	由前一面顶点算起到下一面顶点。
入射角	I	由光线起转到法线。
出射角	I`	由光线起转到法线。
物方孔径角	U	由光轴起转到法线。
像方孔径角	U`	由光轴起转到法线。
物高	y	由光轴起到轴外物点
像高	y`	由光轴起到轴外像点
光线投射高	h	由光轴起到光线在球面的投射点。
像方焦距	f`	由像方主点到像方焦点。
物方焦距	f	由物方主点到物方焦点。
像方焦截距	l`f	由系统最后一面顶点到像方焦点
物方焦截距	lf	由系统第一面顶点到物方焦点。

 

二．  共轴光学系统的结构参数

共轴光学系统的最大特点是系统具有一条对称轴----光轴，系统中每个曲面都是轴对称旋转曲面，它们的对称轴均与光轴重合，如下图所示。

 

 

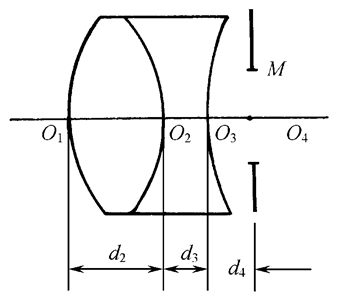
在上图中，各曲面之间的相对位置，依次用它们的顶点之间的距离d表示。

 

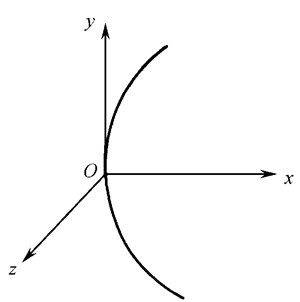
如上图，在计算机里建模时，以曲面和光轴的交点O建立一个局部执教坐标系xyz，我们认为光轴是x轴，xOy平面是子午面，yOz平面是弧矢面，我们就可以在xyz这个局部坐标系里准确用一个数学方程来描述这个表面的面型。

系统中每个曲面的形状可以用以下方程来表示：

 

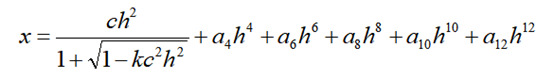
上式中，c为曲面顶点的曲率，K为二次曲面系数，a₄,a₆,a₈,a₁₀,a₁₂为高次非曲面系数。

上式可以普遍地表示球面、二次曲面和高次非曲面。公式右边第一项代表基准二次曲面，后面各项代表曲面的高此项。

基准二次曲面系数K值不同所代表的二次曲面如下表所示：

K值	K<0	K=0	0	K=1	K>1
面形	双曲面	抛物面	椭球面	球面	扁球面

不同的面形，对应不同的面形系数。

球    面：K＝1，a₄=a₆=a₈=a₁₀=a₁₂=0

二次曲面：K≠1，a₄=a₆=a₈=a₁₀=a₁₂=0

实际光学系统中，绝大多数表面面形均为球面，在计算机程序中为了简便直观，对球面只给出曲面半径r（r=1/c）一个参数。

对于平面，相当于半径无限大的球面。

对于非球面，除给出曲率半径r外，还要给出面形系数K，a₄,a₆,a₈,a₁₀,a₁₂的值。

系统中各曲面之间介质的光学性质，用它们对指定波长光线的折射率n表示。

为了全面评价系统的成像质量，一般选出3-5个波长，分别给出系统中各介质对这些波长光线的折射率，然后计算每个波长的像质指标，综合判定系统的成像质量。

对单色光成像的光学系统，只需要计算1个波长即可；

对于人眼观察的目视光学系统，一般采用C(656.28nm)，D(589.30nm)，F(486.13nm) 3种波长；

用感光底片接收的照相机镜头，则采用C，D，g(435.83nm)这3种波长。

至此，有了系统的结构参数（各个曲面的面型参数、各面顶点间距d、每种介质对指定波长的折射率n），再给出入射光线的位置和方向，系统的焦距和主面位置就相应确定了。

三．  光学特性参数

（1）物距L

同一个系统对不同位置的物平面成像时，它的成像质量是不一样的。

一个光学系统只能用于对某一指定的物平面成像。离开这个位置的物平面，成像质量会下降。

因此，在设计一个光学系统时，必须明确该系统是用来对哪个位置的物平面成像的。

表示物平面位置的参数是物距L，它代表从系统第一面顶点O₁到物平面A的距离，符号是从左向右为正，反之为负。

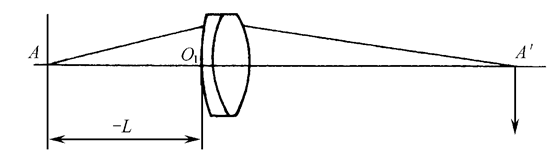
当物平面位在无限远时，在软件中用infinite表示。

如果物平面与第一面顶点重合，则用一个很小的数值代替，如10^-5mm。

（2）物高y或视场角ω

实际光学系统不可能使整个物平面都清晰成像，只能使光轴周围一定范围内成像清晰。

在设计光学系统时，必须指定出它的成像范围。

表示成像范围有两种方式

a）    当物平面位在有限距离时，成像范围用物半高y表示。

b）    当物平面位于无限远时，成像范围用半视场角ω表示。

 

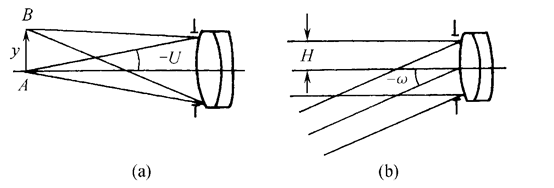
（3）物方孔径角正弦（sinU）或光束孔径高（h）

实际光学系统口径是一定的，只能对指定的物平面上光轴周围一定范围内的物点成像清晰，而且对每个物点进入系统成像的光束孔径大小也有限制。

在设计光学系统时，必须给出符合要求的光束孔径。

a）当物平面位在有限距离时，光束孔径用轴上点边缘光先和光轴夹角U的正弦（sinU）表示。

b）当物平面位在无限远时则用轴向平行光束的边缘光线孔径高（h）表示。

 

（4）孔径光阑或入曈位置

对于轴外物点，限制光束的孔径光阑的位置不同，轴外物点进入系统成像的光束也不同了，成像质量当然也就不同了。

所以，在评价轴外物点的成像质量时，必须给定入瞳或孔径光阑的位置。

入瞳位置用从第一面顶点到入瞳面的距离lz表示，符号规则是向右为正，向左为负。

如果给出孔径光阑，则把光阑作为系统中的一个面处理，并指出哪个面是系统的孔径光阑。

 

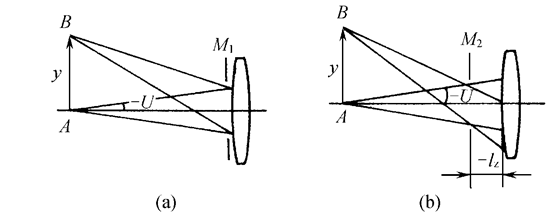
（5）渐晕系数或系统中每个面的通光半径

实际光学系统视场边缘的像面照度一般允许比轴上点适当降低，也就是轴外子午光束的宽度比轴上点光束的宽度小，这种现象叫作“渐晕”。

允许系统存在渐晕有两个方面的原因：

A）    为了保证轴外点的成像质量，把轴外子午光束的宽度要适量减小。

B）    从系统外形尺寸上考虑，为了减小某些光学零件的直径，也需要把轴外子午光束的宽度减小。

表示系统渐晕状况有两种方式：

A）    渐晕系数法。

渐晕系数法是给出指定视场轴外点成像光束的上下光的渐晕系数。

 

 

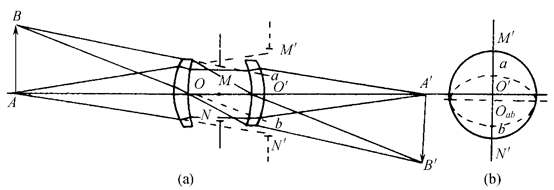
如上图，孔径光阑在物空间的共轭像为入瞳，轴上点A的光束充满了入瞳，轴外点B的成像光束由于孔径光阑前后两个透镜同光直径的限制，使子午面内的上光和下光不能充满入瞳，因此存在渐晕。

从侧视图可以看到实际通光情况，直径为M`N`的圆为轴上点的光束截面，子午面内上光的宽度为O`a，下光的宽度为O`b，对应上、下光的渐晕系数为

 

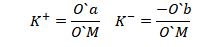
这时实际子午光束的中心为O_ab，一般我们把有渐晕的成像光束截面近似用一个椭圆代表，如上图中的虚线所示。

椭圆的中心为a，b的中点O_ab，它的短轴为

 

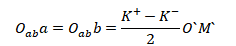
椭圆的长轴为弧矢光束的宽度，一般近似等于O`M`。

用这样的椭圆近似代表轴外点的实际通光面积来进行系统的像质评价。

B）    给出系统中每个通光孔的实际通光半径

这就是给出系统中每个曲面的通光半径h，计算机通过计算大量光线确定出能够通过系统成像的实际光束截面。

这种方式主要是用于最终设计结果的精确评价。

 

总结：有了系统结构参数和光学特性参数，利用近轴光线和实际光线的公式，用光路计算的方法即可计算出系统的焦距、主面、像面和像高等近轴参数，也能对系统在指定工作条件下进行成像质量评价。

 

审核编辑 ：李倩