浅析永磁电机的功率因数

本文先讨论永磁电机的功率因数，然后说一说电源类型不同导致电机分析方法的不同，最后再聊聊内置式永磁电机的一些特点。没有明确的主题，想到哪就写到哪。

如何提高永磁电机的功率因数？时间不够的朋友记住下句话即可。为了提高接工频电源的电机（如异步起动永磁电机）的功率因数，可以在设计阶段调整电机数据；如果电机已经做好，可以调节电源电压。而对于变频器驱动和控制的永磁电机，功率因数与控制方法有关，一般我们不用care它。

一、工频电源供电时

以隐极电机（表贴式）为例讨论。在设计阶段，已知电机的电磁功率Pe和相电压Un；为了使电机的功率因数等于1，即希望电流I与电压U同相位，且可以计算出电流的数值In。这时忽略定子电阻时，电枢反应电动势Ea与电压U垂直并指向U。根据电压方程

Un=E0+Ea=E0+j*Xs*In

电动机运行，Un超前空载反电势E0的角度（即功角）为δ，画出此时的相量图

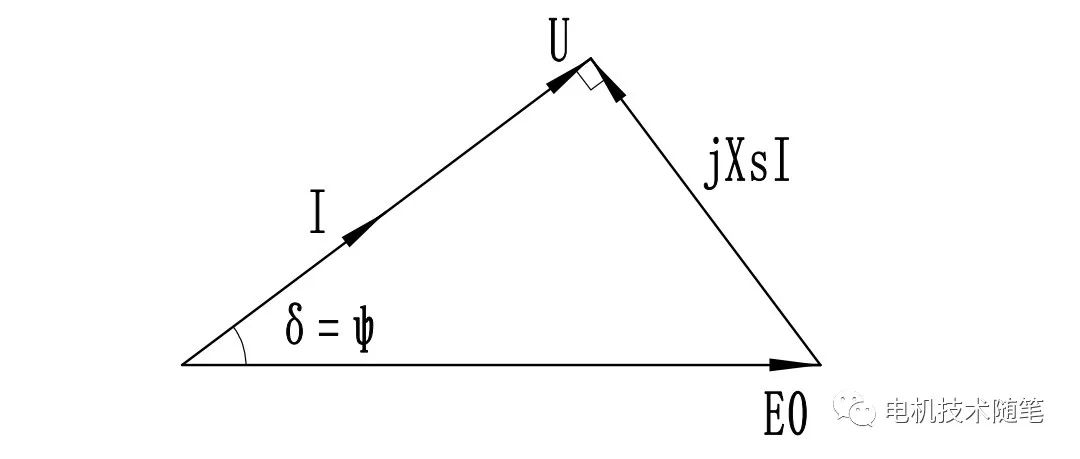
由此可见，若电机的同步反应电抗Xs确定，功率因数等于1时的激磁电动势

E0=√[U^2+(Xs*In)^2]

所以电机的空载反电势要大于电源电压。对于凸极电机（内置式），因为凸极率、功角不确定，很难定量分析，不过可以按上图做定性讨论。假设电流与E0的夹角不变仍为δ（其实是内功率因数角，用ψ表示，习惯上δ特指功角），因为凸极电机Lq>Ld，与隐极电机Lq=Ld相比，交轴电枢电势LqIsinψ会大一些，而直轴电枢电势LdIcosψ会小一些；所以总体而言可以得出两个判断：1、电压可能会超前电流一些，也可能会滞后电流一些，但是不会偏差太大，适当的调整参数可以实现功率因数等于1；2、凸极电机的电压要大一些，一定情况下，可能会大于空载反电势。

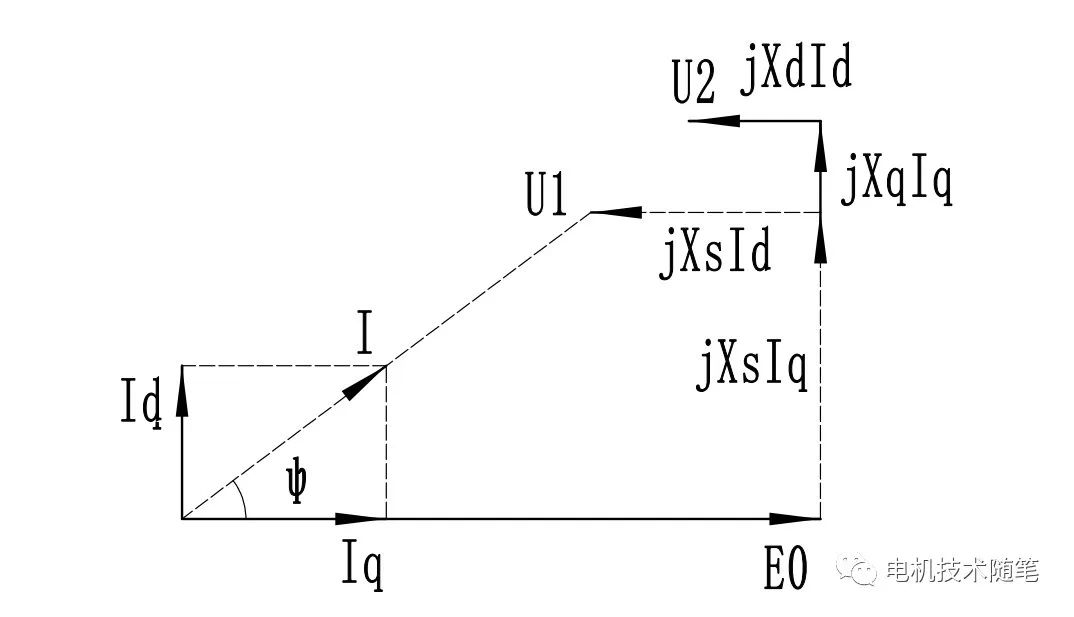
电机做好后，本身的数据已无法更改，只能调节电压使其功率因数等于1。以功角δ为参变量，根据第一个相量图，可以看出

Un=E0*cosδ；In=E0*sinδ/Xs

由Pe=3UnIn可得

Pe=3E0cosδE0sinδ/Xs=1.5*E0^2*sin2δ/Xs

根据此式可以求出δ，然后就可以得到电机需要的相电压Un。

二、变频器供电时

变频器的控制方法非常丰富，同时输出的电压、电流大小受变频器的容量限制。暂且认为变频器的容量足够，通常采用最大转矩电流比（MTPA）的控制策略。即当转矩要求一定时，希望用最小的电流满足，因为电流最小意味着定子铜耗最小；而电流一定时，希望能输出最大的转矩，以尽可能的满足工况需要。仍以模型较简单的隐极电机为例，它的转矩T与电流I之间满足

T=3pψfIsinθ

上式就是表贴式永磁电机的矩角特性公式。式中p为电机的极对数，ψf表示永磁体磁链，θ是电流与转子磁链之间的夹角，称为矩角。

上式表明，要想使电流I产生最大的转矩，令转矩角等于90度即可。用凸极电机双反应理论的说法，电流要全部作用在交轴上，即Iq=I，这就是传说中的Id=0控制。画出相量图，

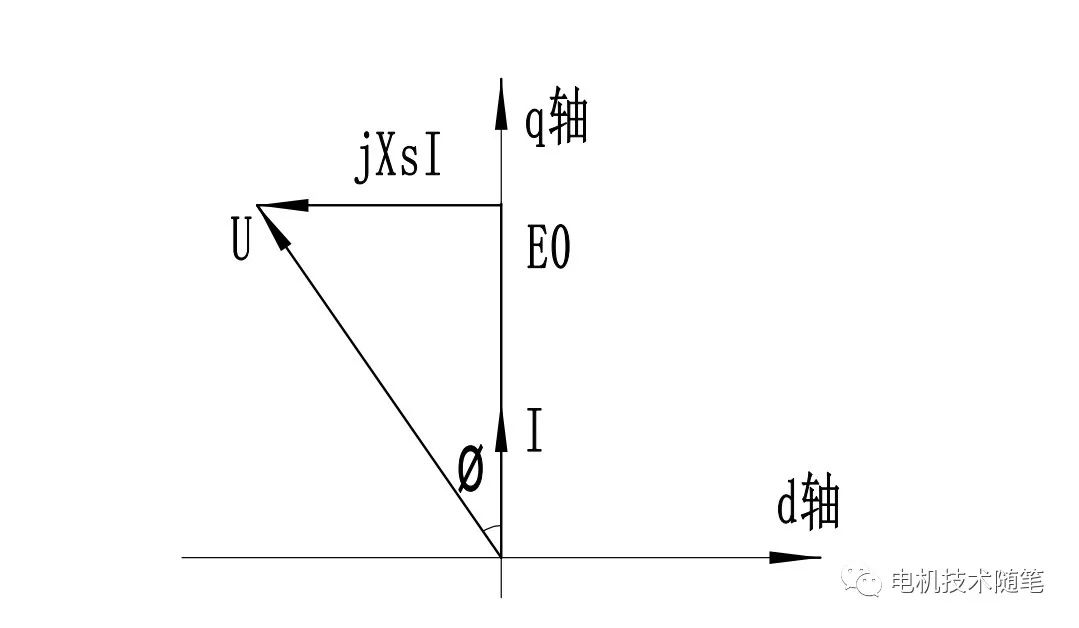
可以看出，电机的功率因数角φ取决于电流磁链与永磁磁链之比，即

tgφ=Ls*I/ψf

所以电流越大，功率因数越小，直到电流I或电压ω*√[ψf^2+(Ls*I)^2]超出变频器的容量为止。

三、电源条件不同时分析方法的区别

可以看出尽管电机参数均已确定，但供电方式不同，分析电机的角度也有区别。对于工频电源，因为电压是已知的，所以我们关心功角随负载转矩的变化规律，用电机的功角特性来研究较为方便。而变频器控制的电机，输入的是经换算后的电流矢量，所以我们关心矩角随负载转矩的变化规律，用电机的矩角特性来研究比较方便。两者的区别在于着眼点是电压还是电流。《电机学》教材大部分篇幅是从电压的角度考虑的；即使到目前，仿真软件在做磁路计算时给的定额也是电压。所以设计变频永磁电机时需要特别注意的是，计算单上的运行状态往往与实际不符，我们也没有必要保证电机在额定运行时功率因数到1。当然有的软件做电磁场有限元分析时可以选择控制方式，施加电流源，这样的仿真结果是更可信的。

四、内置式变频调速永磁电机的最佳工作点

考虑到直交轴电感不相等产生的磁阻转矩，内置式永磁电机的矩角特性为

T=3 p [ψfIsinθ+0.5*(Ld-Lq)I^2sin2θ]

在电机参数p,ψf,Ld,Lq都确定时(Ld

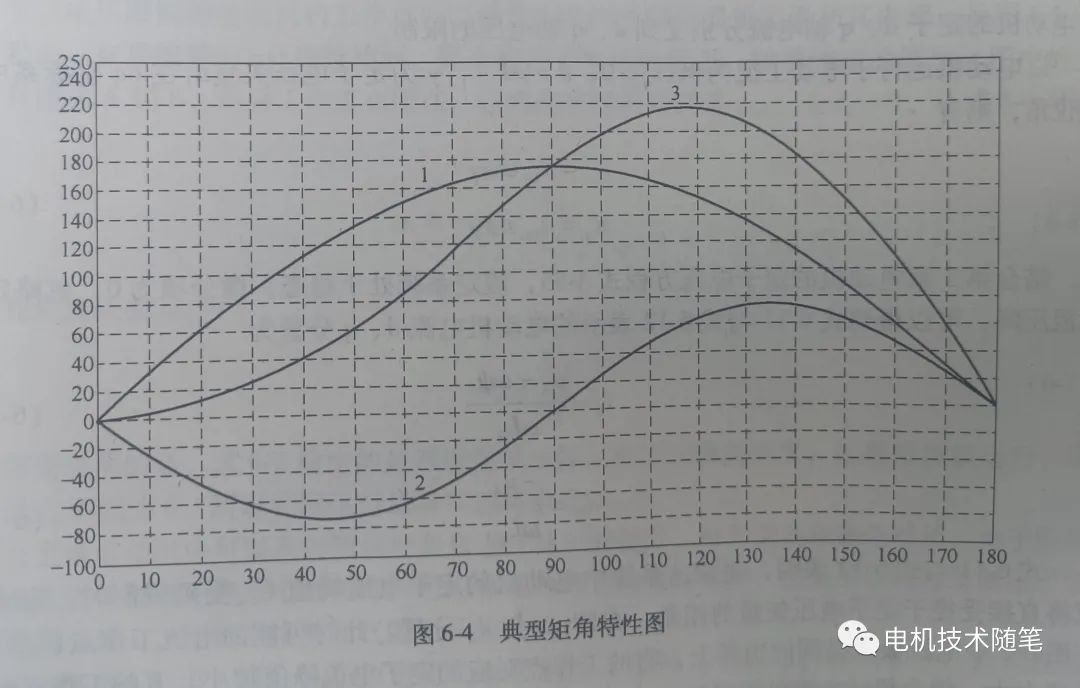
图中曲线1为永磁转矩，曲线2为磁阻转矩，曲线3为曲线1和2的合成。

为了求最大转矩时的θ值，我们按上式令T对θ求导，并使dT/dθ=0,得

cosθ-(Lq-Ld)Icos2θ/ψf=0

因为cos2θ=2*(cosθ)^2-1，并令K=(Lq-Ld)*I/ψf，有

2 K (cosθ)^2-cosθ-K=0

解这个二元一次方程，并根据上图θ角在90~180度之间，即cosθ应为负值，得

cosθ=[1-√(1+8K^2)]/(4K)

好吧，我承认算不下去了-_-||

不过可以换个思路考虑，有不一样的收获。把Id=I*cosθ，Iq=I*sinθ代入转矩公式，得

T=3 p [ψf*Iq+(Ld-Lq)IdIq]

为考察T一定时，Id和Iq的对应关系，有

Iq=1/(3*p)*T/[ψf+(Ld-Lq)*Id]

当Id=0时，Iq=1/(3*p)*T/ψf；当Id=ψf/(Lq-Ld)时，Iq为无穷大。所以把Id作为横轴，Iq作为纵轴，这是一组双曲线，我们只关心上半轴，因为此处Iq>0，转矩为正。画出曲线如图所示

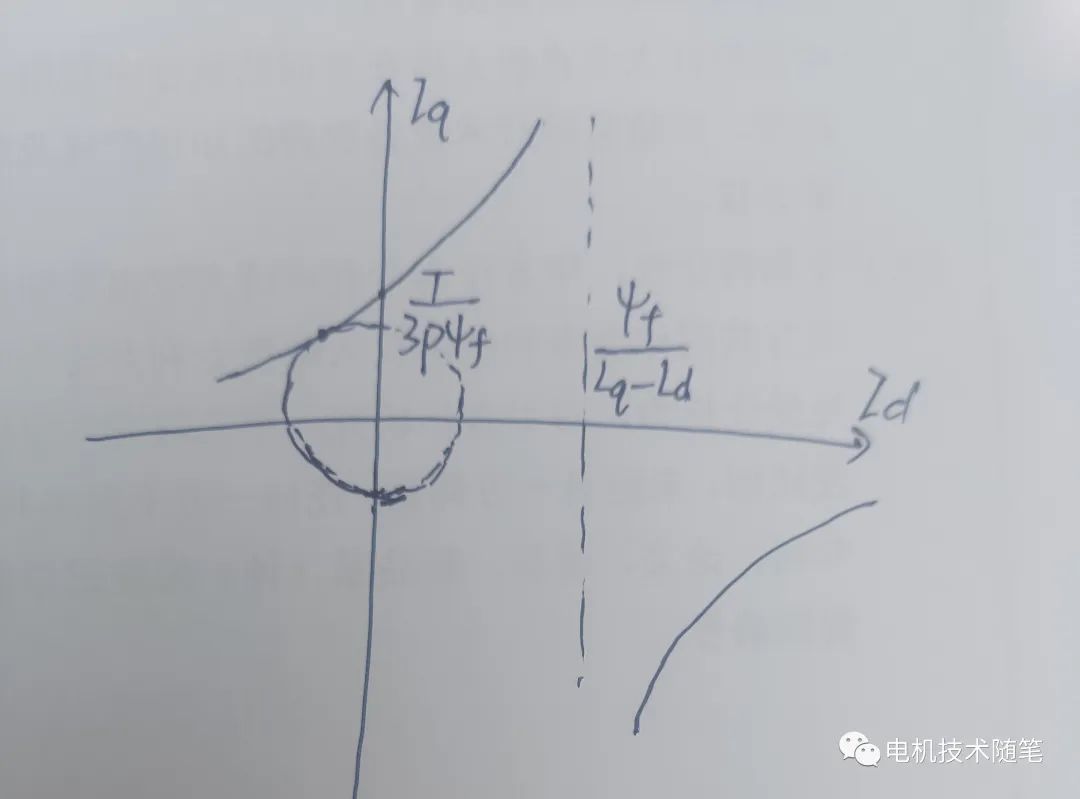
显然，这条曲线有一点距离原点最近，即该点的电流I=√(Id^2+Iq^2)最小，是MTPA控制算法求得的工作点。该点矢量与横轴的夹角也是上述二元一次方程cosθ的解。

把Is从零到最大值每个电流下的最大转矩点连起来，得到的就是MTPA曲线。如下图所示。可以看出，随着转矩的增加，直轴电流占总电流的比例随之增大。