

互感电感的串并联计算方法
应用电子电路
描述
我们讨论了电感元件的串并联的计算,今天我们进行深入学习探讨互感电感的串并联计算问题,那互感电感串联和电感并联时总电感量怎么算呢?在了解互感电感串并联之前,先必须知道电感的互感、互感系数等知识。
互感
1、互感电感的互感现象:如图1所示,设两个线圈L1和L2,当L1线圈通入交变电流时,在本线圈产生交变磁通Φ1,并引起自感电压e1;同时,磁通穿过另一个线圈,产生相应互感电压e2,这种现象称为互感现象。
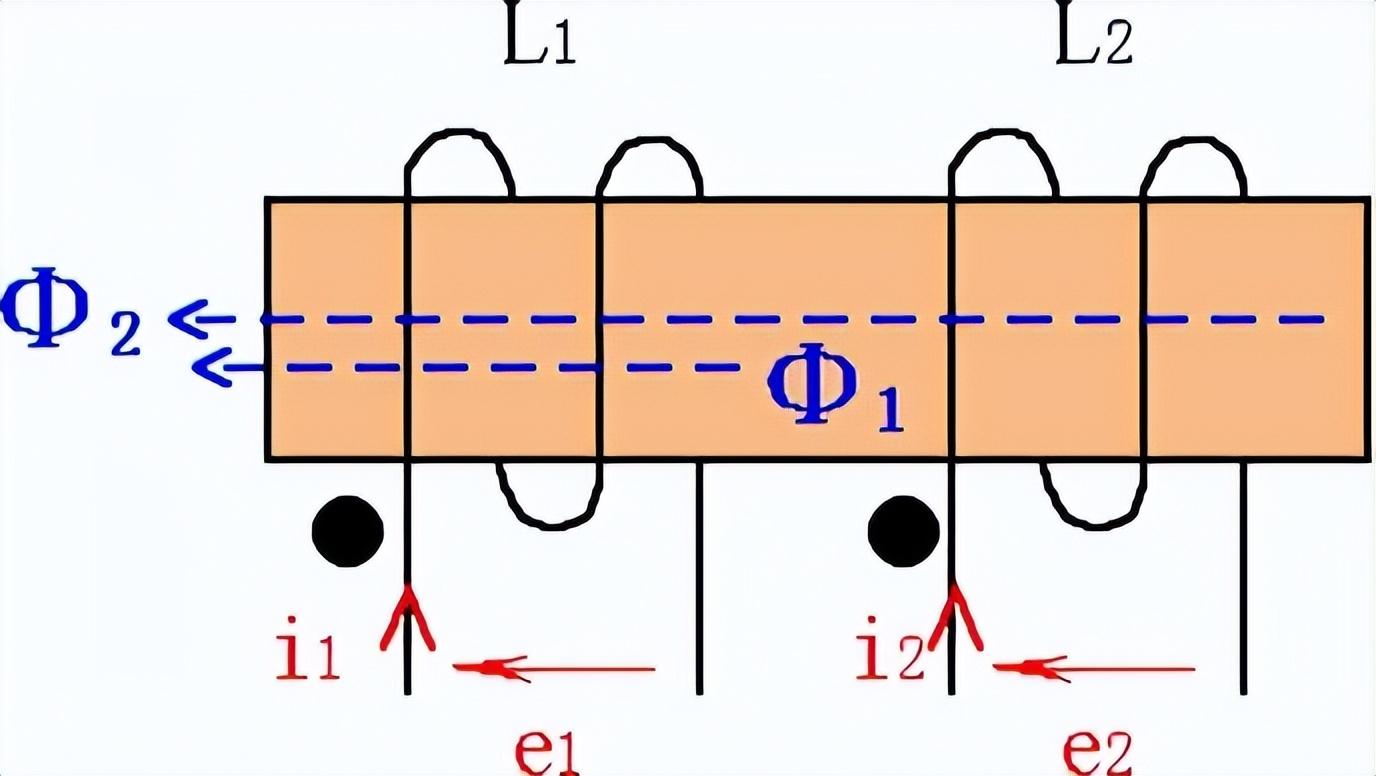
图1 互感电感互感现象
2、互感系数M:互感电感中的“M”称为互感系数,单位和自感系数L相同。
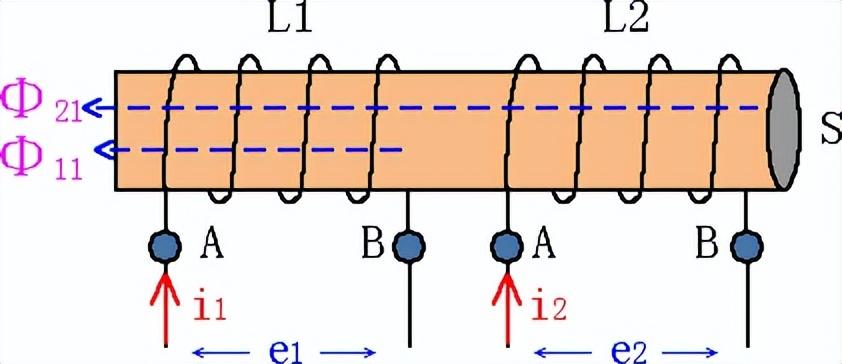
图3 互感系数M
线圈L1中的电流i1变化,引起线圈L2的磁通变化,线圈L2中产生感应电动势e2。穿过线圈2的磁通量ψ21正比于线圈L1中电流i1。
我们定义:
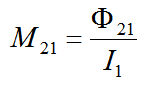
M21是线圈1对线圈2的互感系数,单位亨(H)
那么对于L2、i2一样,则有
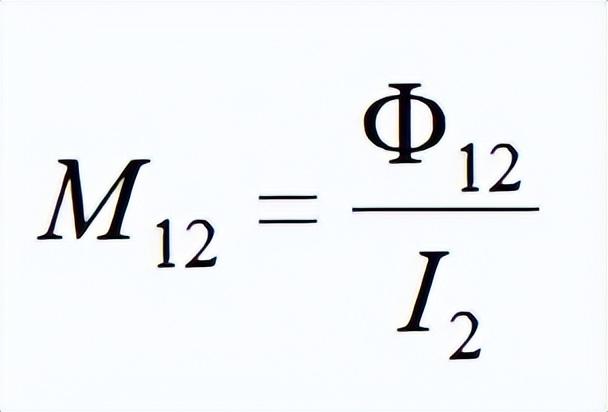
M12表示线圈2对线圈1的互感
若两回路相对位置不变,周围无铁磁性物质,则互感系数M=M21=M12,则
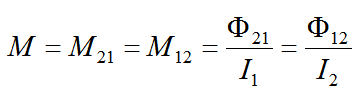
注意:中Φ21为通过线圈2的磁通量,I1为通过线圈1的电流:中Φ12为通过线圈1的磁通量,I2为通过线圈2的电流
在工程上为了定量地描述两个耦合线圈的耦合紧密程度,常用常数k表示耦合系数:
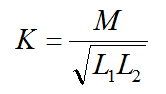
k表示耦合系数,M为互感系数,L1为线圈1电感量,L2为线圈2电感量
通常情况下:
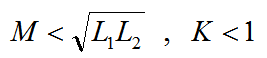
当一个线圈产生的磁通全部穿过另一个线圈,这种情况称为全耦合即理想状态K=1。
3、同名端与异名端:如图4所示,绕在同一铁心柱上,相对绕向相同的端子。各绕组的同名端,电流同时流入或者同时流出。用一对符号“•”予以标注。如下图中1、3互为同名端,2、4互为同名端;1、4互为异名端,2、3互为异名端。互感电压取“+”,反之取“-”。
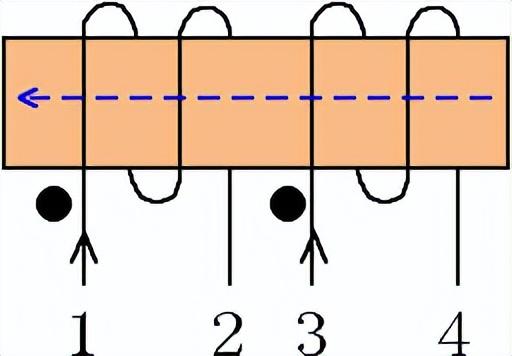
图4 同名端与异名端
互感电感的串联
由于同名端的存在,具有互感的两个线圈串联的电路,就有两种接法: 即一种是同向串联,如图5所示,另一种是反向串联,如图6所示。
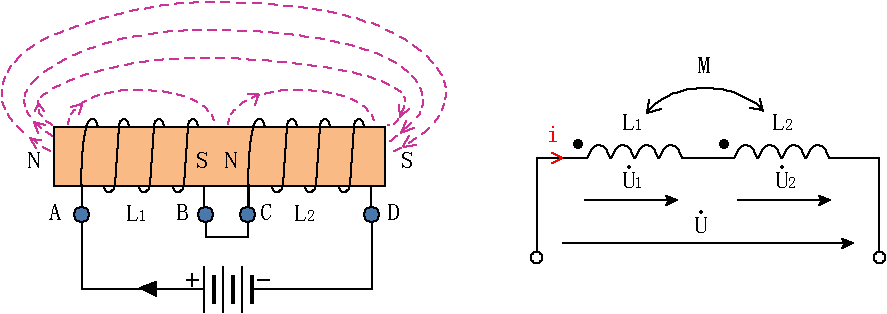
图5 同向串联
(1)同向串联:如图5所示。把两线圈的异名端相连,电流从同名端流入、异名端流出,这种连接方式称为同向串联。
依据图5中所示参考方向可列出两线圈的伏安关系:
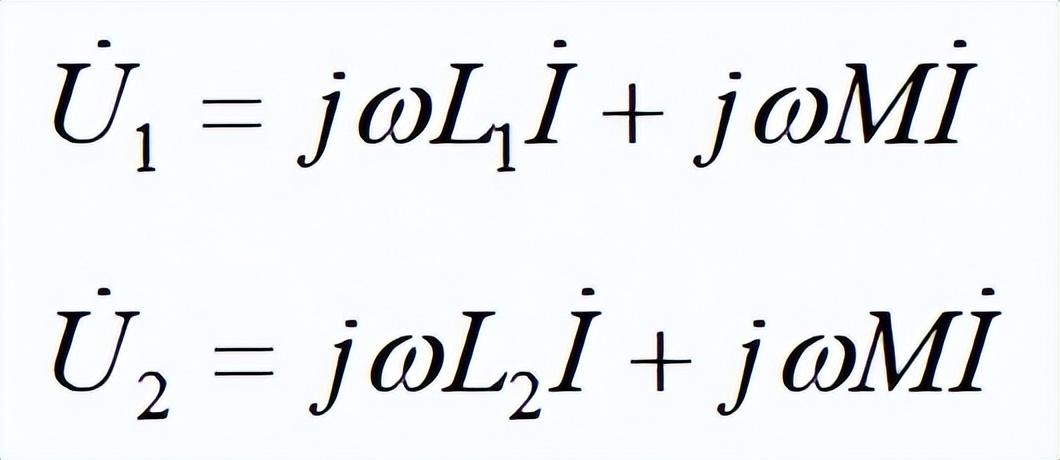
串联后电路两端总电压为:
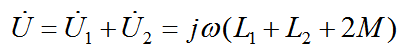
所以,当它们同相串联的时候,对应的电感量为:

(2)反向串联:如图6所示。把两线圈的同名端相连,电流从同名端流入、异名端流出,这种连接方式称为反向串联。
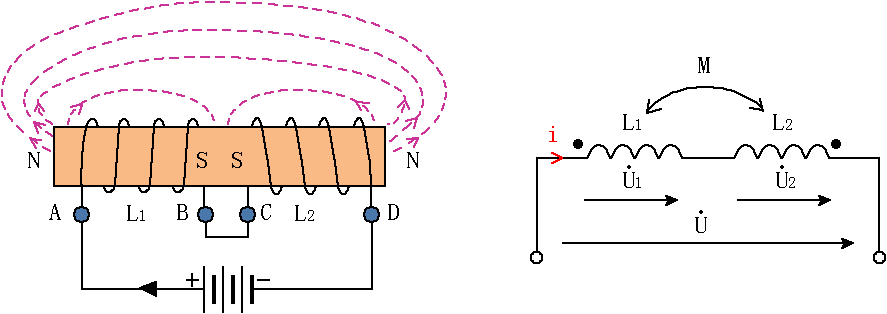
图6 反向串联
如果是反向串联的时候,按照相同的方式,可以证明对应的等效电感量为:
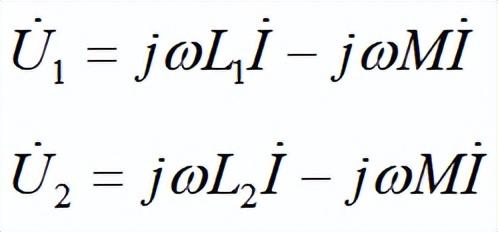
串联后电路两端总电压为:
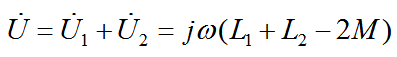
所以,当它们反向串联的时候,对应的电感量为:
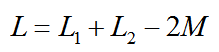
互感电感的并联
两个互感线圈并联时,也有两种情况,一种是两个线圈同名端相连,称同向并联,如图7(a)所示;另一种为两个线圈的异名端相连,称反向并联,如图7(b)所示。
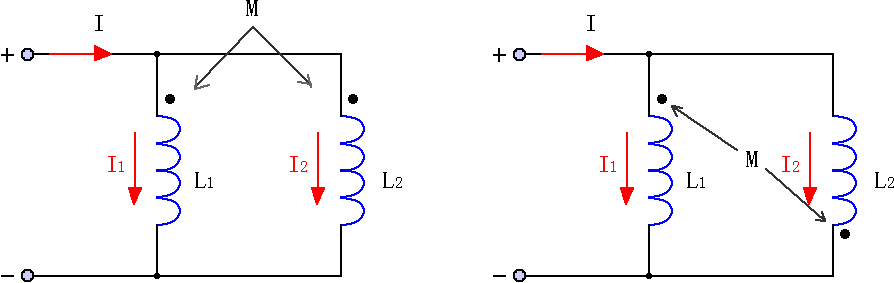
图7(a) 图7(b)
(1)同向并联:当选择电流为图示参考方向时,则在正弦电路中有:
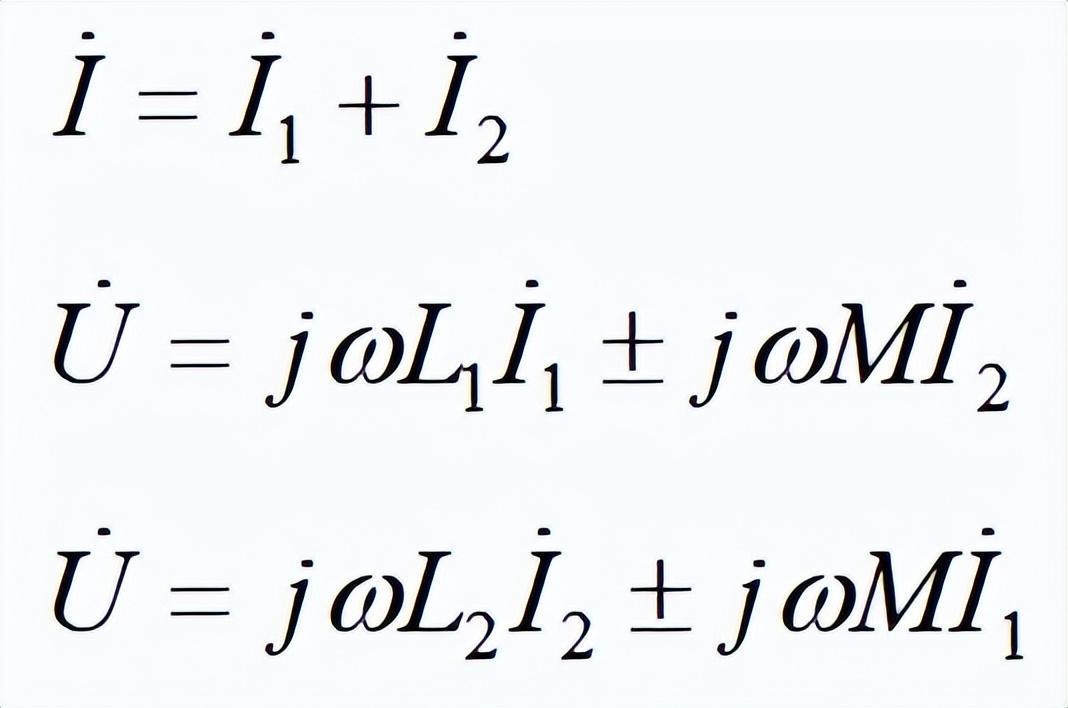
式中互感电压前的正号对应于顺并,负号对应于反并。求解可得并联电路的等效复阻抗Z为:
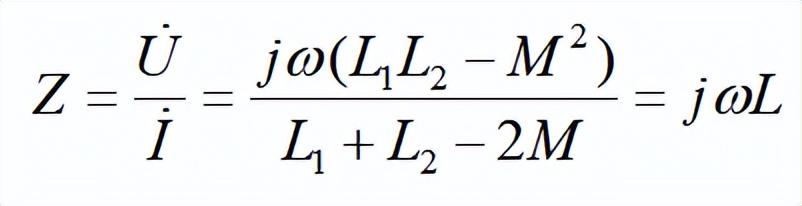
同向并联的等效复阻抗Z
L为两个线圈同相并联后的等效电感,即
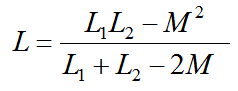
同向并联等效电感
(2)反向并联:如7(b)所示,式中互感电压前的正号对应于顺并,负号对应于反并。求解可得反向并联电路的等效复阻抗Z为:
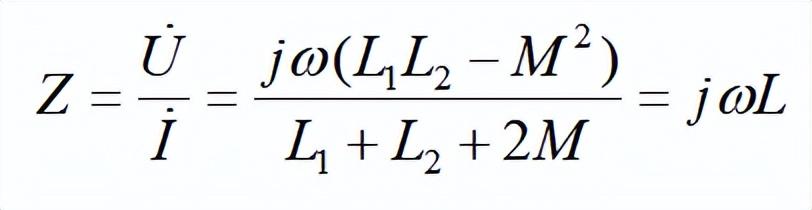
反向并联电路等效复阻抗Z
L为两个线圈反相并联后的等效电感,即
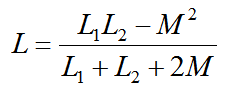
反相并联等效电感
例题1:如图8所示,两个线圈电感L分别为0.1H、0.2H,互感系数为0.2H,求总电感。
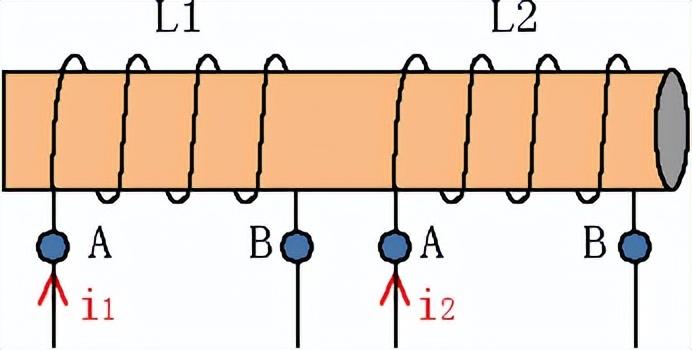
图8
解:两个串联电感是同向串联,则等效互感电感L为:
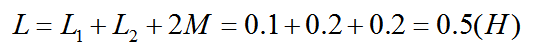
例题2:如图9所示为理想互感电感,两个线圈为电感L分别为0.2H、0.8H,求互感系数和总电感。
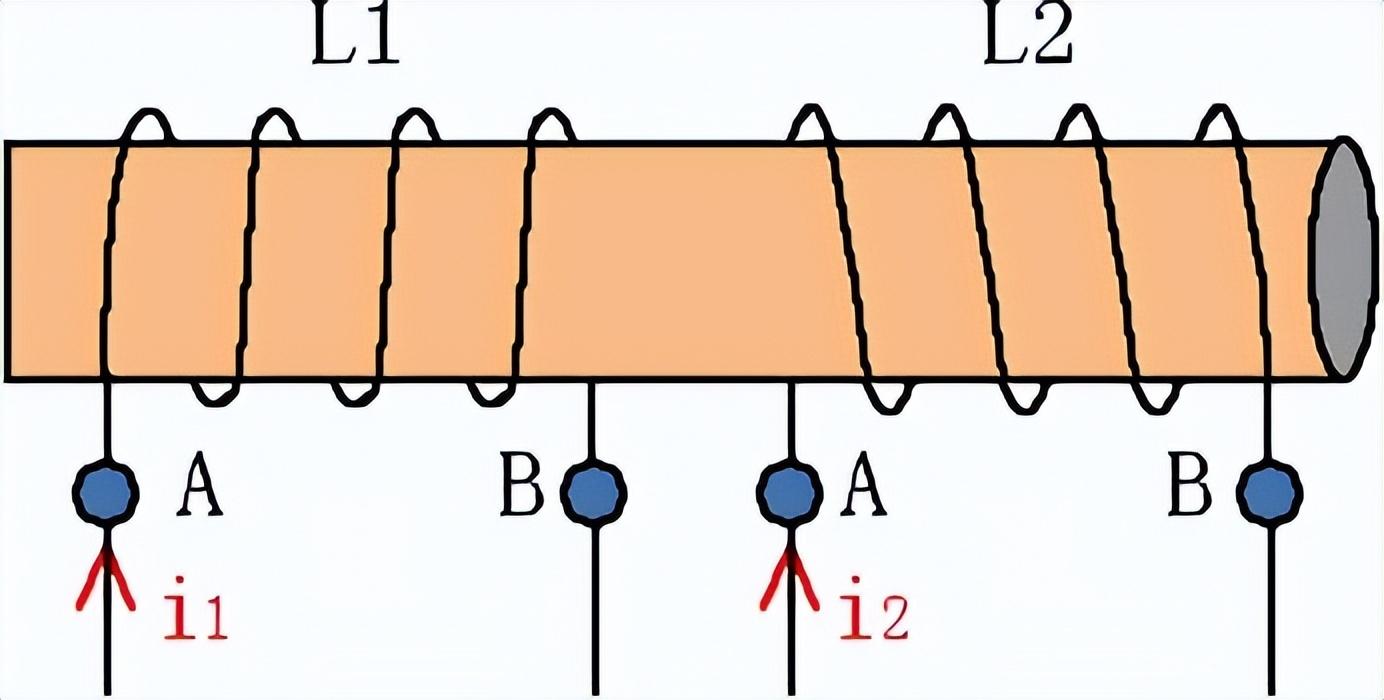
图9
解:由于是理想互感电感,则耦合系数K=1,则互感系数为:
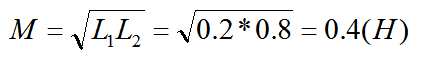
由于两个串联电感是反向串联,则等效互感电感L为:
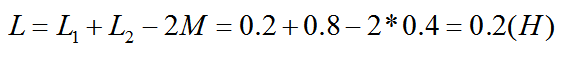
例图分析:如图10所示,线圈电感L1分别为0.2H,互感系数为0.4H,总电感为0.6H,求电感L2大小。答案在评论区见!
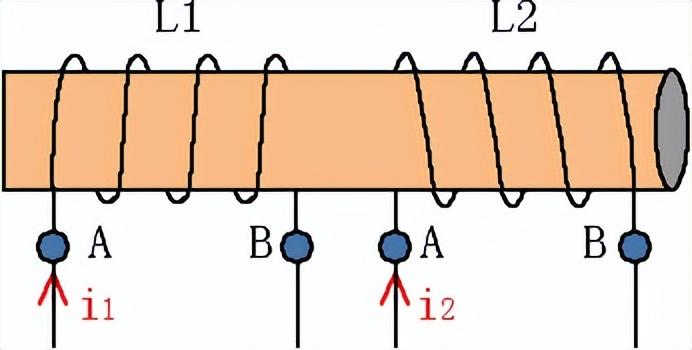
图10
-
 jf_09072817
2024-05-31
0 回复 举报byd内置浏览器,我怎么打开才能算在APP内打开? 收起回复
jf_09072817
2024-05-31
0 回复 举报byd内置浏览器,我怎么打开才能算在APP内打开? 收起回复
-
并联谐振串联谐振计算方法介绍2020-06-19 5417
-
怎样去计算有互感电感串并联的等效电感2021-08-31 10461
-
互感电路测量2008-09-24 15390
-
电容的串并联计算方法2008-12-13 122753
-
电压为12伏的led串并联用限流电阻计算公式2011-07-01 18242
-
电感资料--电感的计算方法2016-10-10 1013
-
任意空间位置线圈的互感计算方法_谢岳2017-01-08 606
-
串并联电路的特点与识别串并联电路的四种方法2017-05-02 68817
-
串并联电路中的等效电阻计算公式2018-01-16 7009
-
电阻串联和并联的计算方法_电阻串联和并联的作用2018-01-21 219101
-
BUCK电路中电感的计算方法2023-03-16 17586
-
零序互感器的变比计算方法2023-06-03 10766
-
变压器电感计算方法 变压器感抗如何计算2023-08-23 8862
-
耦合电感的互感电压怎么判断好坏2024-03-09 2056
-
电容电感并联阻抗的计算方法2024-07-17 13738
全部0条评论

快来发表一下你的评论吧 !

