

电感在LC滤波电路的工作原理
应用电子电路
描述
前几天我们学习了电感滤波作用,今天我们继续深入探讨电感在实际电路工作中电感的滤波电路的应用问题,下面我们来看一看LC滤波电路的工作原理。
在手机应用电路中,需要通过天线接收的无线电信号进行滤波,再送到后期低噪音放大器电路进行放大处理,除了手机外还有收音机、电视机、对讲机等无线接收发射设备,LC滤波器具有结构简单、设备投资少、运行可靠性较高、运行费用较低等优点,应用很广泛。常见滤波器有高通滤波器、低通滤波器、带通滤波器、带阻滤波器等这几种,下面我们一起来看看!
1、CL滤波电路:
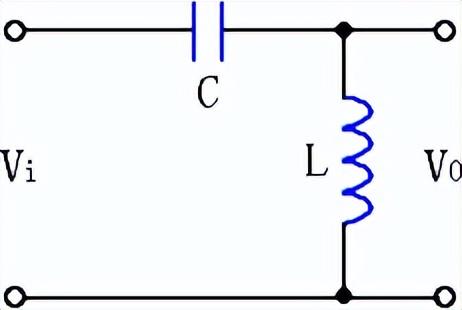
图1 基本LC高通滤波器
如图1所示是一种典型的基本CL滤波电路,设输入信号电压为Vi,角频率为ω,输出信号电压为V0,由于电感感抗、电容容抗分别为:
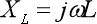
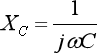
由于电感L与电容C串联,则有:
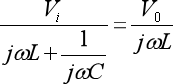
化简后:
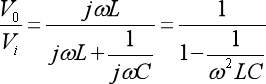
我们把V0/Vi设为输出比输入的电压比称为放大倍数dB,dB最大值为1或者-1(-1表示输出与输入反向关系),最小值为0。当dB=±1表明输出响应最好,V0≈±Vi;反之,当dB=0表明输出响应最差,几乎没有输出,V0≈0。图2为CL滤波电路频率响应关系图。
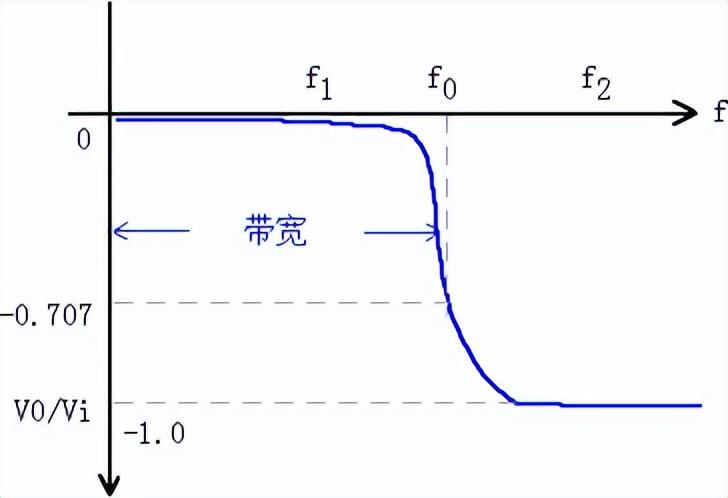
图2 CL滤波电路频率响应关系图
由于电感感抗较小,电容容抗较大,再通过上式和CL滤波电路频率响应关系图表明:
(1)当角频率为ω较小即输入信号频率较小时,ω2LC也较小,V0/Vi的值越来往0靠近,即输出信号V0也越来越小,几乎接近与0,此时表现为低频信号不容易通过。
(2)当角频率为ω较大即输入信号频率较大时,ω2LC也较大,V0/Vi的值越来越大往-1靠近,即输出信号V0接近与Vi,此时表现为高频信号很容易通过。
即当ω2LC>1,ω>1/√LC时,该电路表现为低阻态,频率越高,阻抗越小;反之当ω2LC<1,ω<1/√LC时,该电路表现为高阻态,频率越低,阻抗越大。
故此该电路截止角频率ω为1/√LC,截止频率f0=1/2π√LC,此时V0/Vi值=-0.707,高于该截止频率f0的信号容易通过,而低于该频率的信号就不容易通过,所以该电路属于高通滤波器。
2、LC滤波电路:
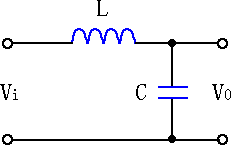
图3 基本LC滤波电路
如图3所示是一种典型的基本LC滤波电路,同样设输入信号电压为Vi,角频率为ω,输出信号电压为V0,由于电感感抗、电容容抗分别为:
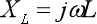
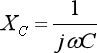
由于电感L与电容C串联,则有:
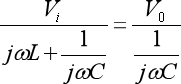
化简后:
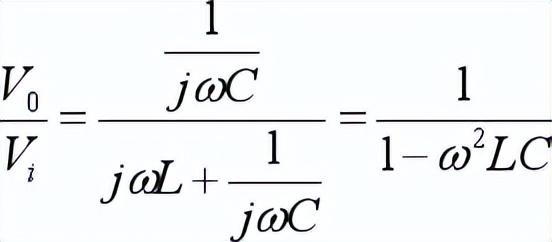
图4为LC滤波电路频率响应关系图。
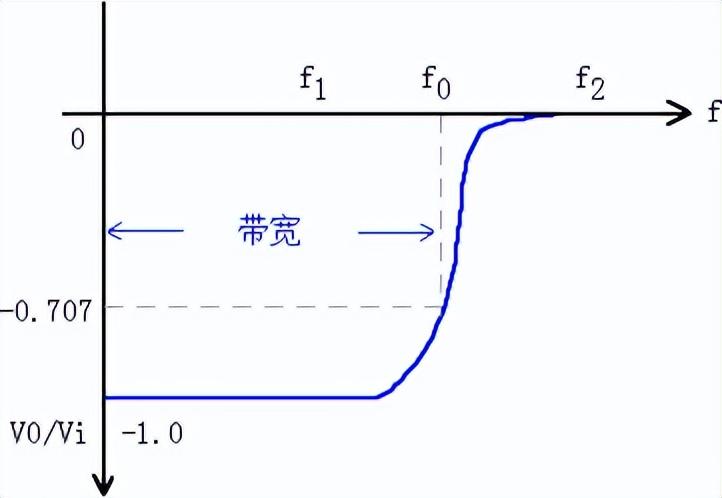
图4 LC滤波电路频率响应关系图
由于电感感抗较小,电容容抗较大,再通过上式和LC滤波电路频率响应关系图表明:
(1)当角频率为ω较小即输入信号频率较小时,ω2LC也较小,V0/Vi的值越来往-1靠近,即输出信号V0也越来越强,几乎接近与Vi,此时表现为低频信号很容易通过。
(2)当角频率为ω较大即输入信号频率较大时,ω2LC也较大,V0/Vi的值越来越大往0靠近,即输出信号V0接近0,此时表现为高频信号很难通过。
即当ω2LC>1,ω>1/√LC时,该电路表现为高阻态,频率越高,阻抗越大;反之当ω2LC<1,ω<1/√LC时,该电路表现为低阻态,频率越低,阻抗越小。
故此该电路截止角频率ω为1/√LC,截止频率f0=1/2π√LC,V0/Vi值=-0.707,高于该截止频率f0的信号不容易通过,而低于该频率的信号就容易通过,所以该电路属于低通滤波器。
3、带通滤波电路:
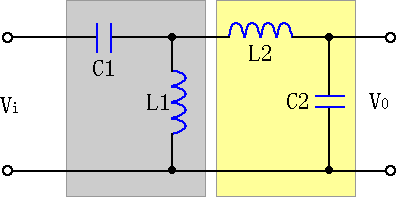
图5 带通滤波器电路
带通滤波器是允许某一频段的信号通过的一种滤波器。如图5所示就可以组成带通滤波器,全半部分是CL高通滤波电路,后半部分是LC低通滤波电路,只要满足全半部分CL高通滤波电路截止频率f01>f02,即:
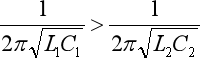
也就是L1C1>L2C2即可,图6为LC带通滤波电路频率响应关系图。
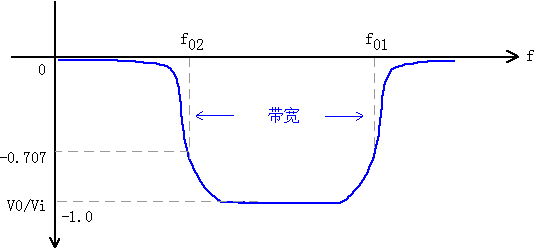
图6 LC带通滤波电路频率响应关系图
4、带阻滤波器:
在图5带通滤波电路设计电路图中如果L1C1
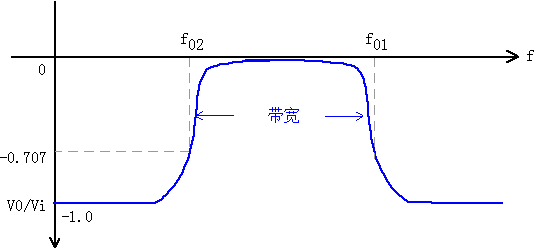
图7 LC带阻滤波器电路频率响应关系图
当然除了上面这些滤波器电路外,还有很多电路,都可以组成高通滤波器、低通滤波器、带通滤波器,比如图8为常见的滤波器。

图8 常见的滤波器
-
LC滤波器与电感、电容的区别:技术分析与应用2025-05-12 1201
-
lc振荡电路电流变化规律 lc振荡电路的工作原理2024-02-18 11650
-
色环电感在电路中的作用 色环电感的工作原理2023-11-29 4118
-
模拟电源处的滤波经常是用LC电路,但是为什么有时LC比RC滤波效果差?2023-11-24 3946
-
LC滤波电路和RC滤波电路的主要区别是什么?2023-11-20 11145
-
lc滤波电路原理,lc滤波器电路图2023-07-19 22193
-
滤波电感的功能和工作原理2023-07-09 7444
-
滤波电路工作原理2019-07-22 3115
-
电阻滤波电路和电感滤波电路工作原理2018-01-15 22322
-
共模电感工作原理2013-01-05 7028
-
电感滤波电路工作原理是什么2011-11-10 9158
-
L 型LC 电源滤波电路模型及工作原理2010-10-22 16180
-
说说LC滤波电路2009-12-02 1442
-
LC滤波电路及原理2008-10-20 38352
全部0条评论

快来发表一下你的评论吧 !

