深度学习和强化学习的重要概念和公式

神经网络(Neural Networks)

神经网络是一类用层构建的模型。常用的神经网络类型包括卷积神经网络和递归神经网络。

结构

关于神经网络架构的描述如下图所示：

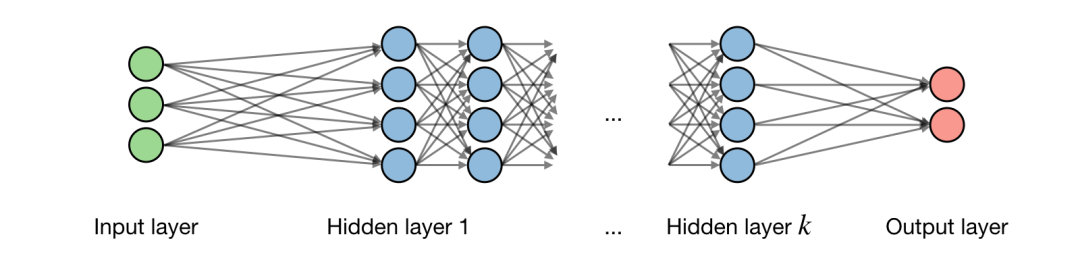
记 为网络的第 层， 为一层中隐藏的第 个 单元，得到：

式中 分别表示权重，偏移和输出。

激活函数

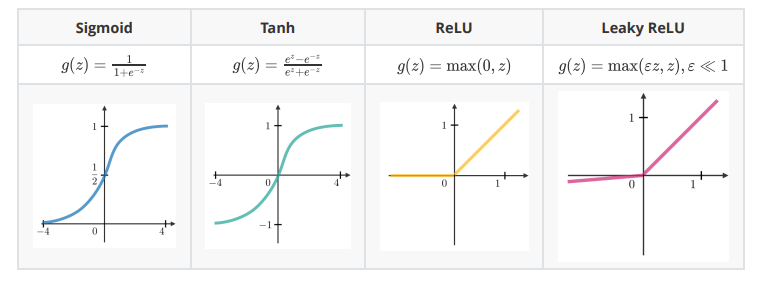
在隐含单元的末端使用激活函数向模型引入非线性复杂性。以下是最常见的几种:

交叉熵损失(Cross-entropy loss)

在神经网络中，交叉熵损失 是常用的，定义如下:

学习率(Learning rate)

学习率通常记作 ，表示在哪一步权重得到了更新。这个可以是固定的，也可以是自适应变化的。目前最流行的方法是 Adam，这是一种自适应学习率的方法。

反向传播(Backpropagation)

反向传播是一种通过考虑实际输出和期望输出更新神经网络权重的方法。权重 的导数用链式法则计算(chain rule)，它的形式如下：

因此权重更新如下：

更新权重

在神经网络中，权重的更新方式如下：

第一步：对训练数据取一批(batch)；第二步：进行正向传播以获得相应的损失；第三步：反向传播损失，得到梯度；第四步：使用梯度更新网络的权重。

丢弃(Dropout)

它是一种通过在神经网络中删除单元来防止过度拟合训练数据的技术。实际应用中，单元被删除的概率是 ，或被保留的概率是 。

卷积神经网络(Convolutional Neural Networks)

卷积层需求

记 为输入量大小， 为卷积层神经元大小， 为 zero padding 数量，那么匹配给定体积输入的神经元数量 为：

批量正则化(Batch normalization)

这一步是超参数(hyperparameter) 正则化批量  。记 分别为批量值的平均值和方差，正则化表示如下：

它通常用于完全连接或卷积层之后，且在非线性层之前。目的是允许更高的学习率，减少初始化的强依赖。

递归神经网络(Recurrent Neural Networks)

门类型(Types of gates)

以下是在我们碰到的典型递归神经网络中存在的不同类型的门：

输入门(Input gate)	忘记门(Forget gate)	输出门(Output gate)	门(Gate)
是否写入神经元？	是否擦出神经元？	是否显示神经元？	写入多少

长短期记忆网络(LSTM, Long Short-Term Memory)

长短期记忆网络是RNN模型的一种，它通过添加“忘记”门来避免梯度消失问题。

强化学习与控制(Reinforcement Learning and Control)

强化学习的目标是让代理(agent)学会如何在环境中进化。

马尔科夫决策过程(Markov decision processes)

马尔科夫决策过程(MDP)是一个5元组 ，其中：

是一组状态。

是一组行为。

是 和 的状态转换概率。

是discount系数。

或者 是算法要最大化的奖励函数。

策略(Policy)

策略 是一个映射状态到行为的函数 。

备注：我们说，如果给定一个状态 ，我们执行一个给定的策略 ，得到的行为是 。

价值函数(Value function)

对于给定的策略 和状态 ，我们定义价值函数如下 ：

贝尔曼方程(Bellman equation)

最优贝尔曼方程描述了最优策略 的价值函数 ：

备注：对于给定的状态 ，我们记最优策略 为：

价值迭代算法(Value iteration algorithm)

算法包含2步：

第一步，初始化价值：

第二步，基于之前的价值进行迭代：

最大似然估计(Maximum likelihood estimate)

状态转移概率的最大似然估计如下:

的行为次数

Q-learning

Q-learning是 一种无模型，公式如下：

　　审核编辑：汤梓红