R-sq越高代表模型拟合越好？

在统计建模中，究竟R-sq应该取多大? 我们经常听到这个疑问。以前，我们分享过如何解释R-Sq，我们还纠正了一个统计上的误区，即较低的R-sq不一定差，较高的R-sq不一定好。显然，“R-sq应该多高”的答案就是：视情况而定。

盲目追求高R-sq的模型很容易掉入过度拟合的陷阱，这一点在大数据建模中经常发现。

什么是好的模型？

我们在建模的时候最不愿意看到两种情况：过度拟合和欠拟合。使用与拟合模型相同的数据来评估模型，经常会导致过度拟合，如下图：

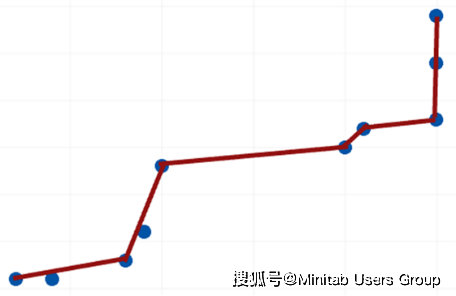
而这种过度拟合的模型如果用来预测的话，效果往往不好。

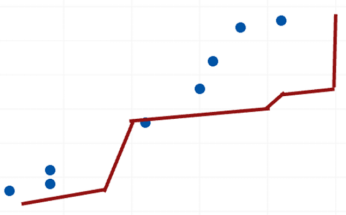
那么什么才算一个好的模型呢？一个好的模型需要在高方差（过度拟合）和高偏差（欠拟合）之间找到一种权衡。

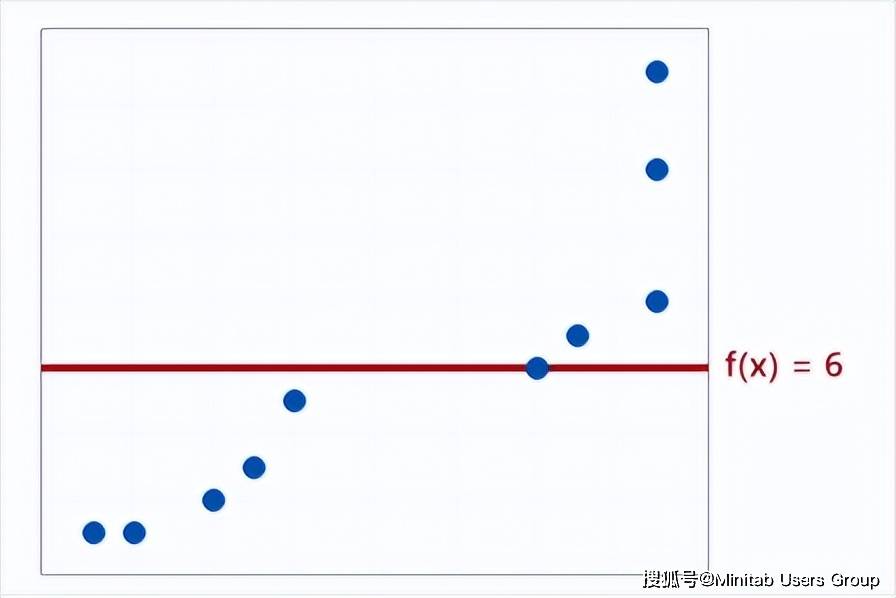
上图就是由于模型太简单导致存在高的偏差。

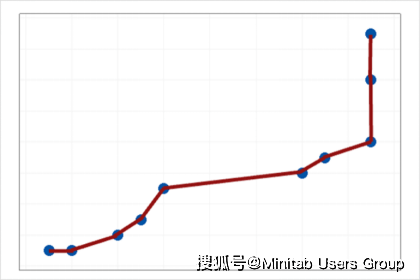
上图就是由于模型过度拟合导致存在高的方差。

过度拟合与欠拟合之间的权衡

那么如何去找到“高偏差”与“高方差”之间的权衡呢？这就需要用到“验证”法了。

大数据建模把数据分为两大类：训练集和测试集。训练集用来创建模型，而测试集来评估模型的性能，这样我们就可以来权衡过度拟合和欠拟合的模型。

举个例子，对于同一组数据我们可以下面三个不同的模型，看起来立方模型是最好的。

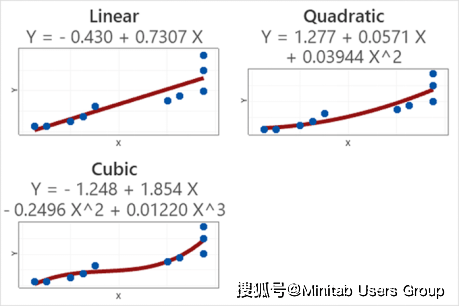
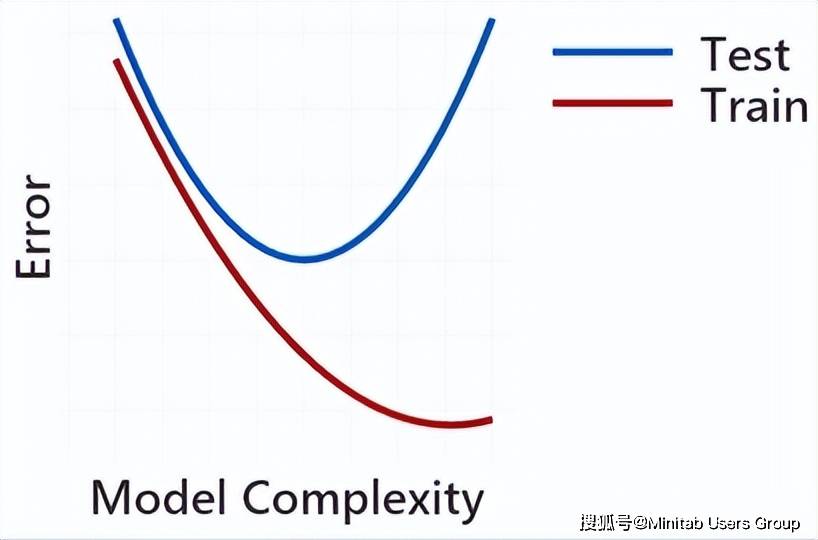
但当我们常用验证法，从下图中我们可知，用训练集来建模时，模型越复杂模型误差确实越小，但再来看看测试集你会发现当模型复杂到一定程度，它的误差会随着模型复杂度的增加而增大。也就是说，太简单和太复杂的模型都不能很好的用来预测。看来找到这个权衡点很重要，这是如何做到的呢？这就要来说说所谓的“验证”法了。

三种验证方法

在Minitab 21版本的回归（拟合回归模型、拟合二值Logistic模型、拟合Poisson模型）和预测分析模块中包含三种用于验证的方法：

对这三种验证方法做一个简单介绍：

1. 留一验证法

这种方法正如其名，留一留一，就是留下一行yi，再用其他所有数据来建模，得到模型后再把留下来这一行代入得到的模型就会得到对应的拟合者，其过程如下所示：

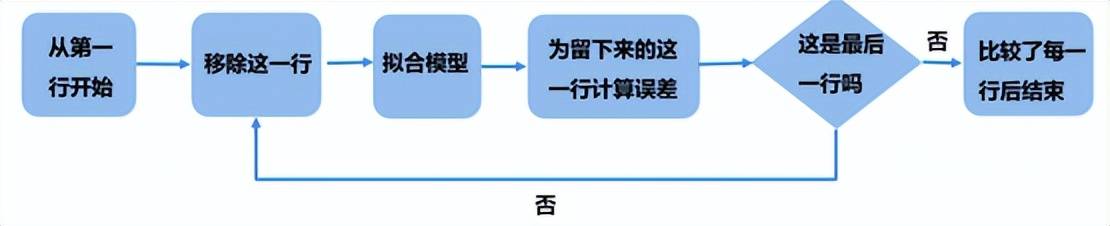
接下来，我们计算预测的残差平方和（Predicted Residual Sum of Squares）

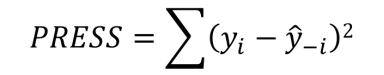
有了PRESS就可以来计算R-sq(预测)了，到这里是不是很熟悉了。

 

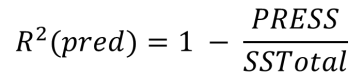
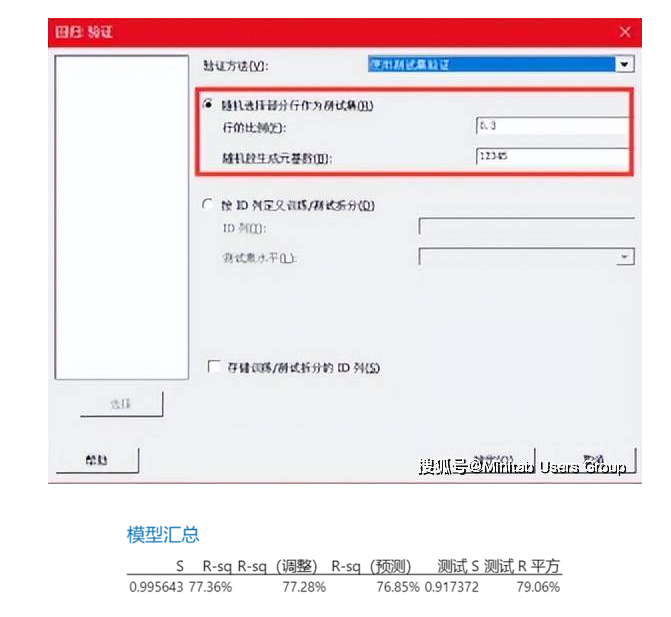
2. 测试集验证法

随机保留一定比例（Minitab 21默认保留30%）的数据（测试集），用剩余的数据来拟合模型（训练集）。

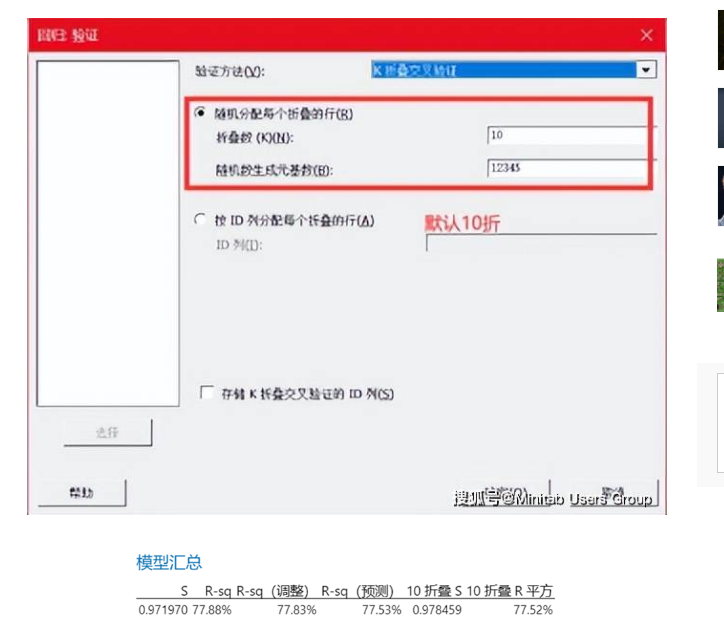
3. K折交叉验证法

将数据拆分个K个子集，以其中一份为测试数据，其它K-1份用于训练数据来拟合模型。使用测试数据计算误差，重复k次，每次忽略一份，基于测试数据误差统计汇总信息选择模型。

小结

当你询问R-sq应该取多大时，可能是因为你想确定当前模型是否能够满足要求。我希望你有更好的方法来解决这这个问题而不是只通过R-sq，尤其当你的数据量和数据维度比较大的时候。

审核编辑 黄宇