

正弦稳态电路的功率计算
描述
01阻抗和导纳
在角频率为ω的正弦电源激励下处于稳态时,端口N0的电流和电压都是同频率的正弦量,其相量分别设为
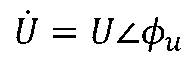
和
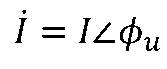
。
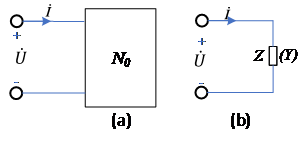
一端口N0的端电压相量与电流相量的比值定义为一端口N0的阻抗Z,即有
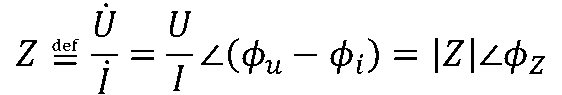
或
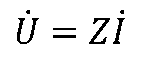
上式是用阻抗Z表示的欧姆定律的相量形式。 Z不是正弦量,而是一个复数,称为复阻抗,其模
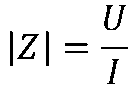
称为阻抗模(经常将Z,| Z|称为阻抗),幅角
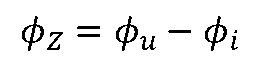
称为阻抗角。 Z的单位为Ω,其电路符号与电阻相同,如下图(b)所示,Z的代数形式为
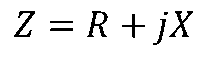
式中R为等效电阻分量,X为等效电抗分量,X>0时称为感性阻抗,X<0时称为容性阻抗。 Z在复平面上用直角三角形表示,如下图(a)所示(图中设X>0),称为阻抗三角形。
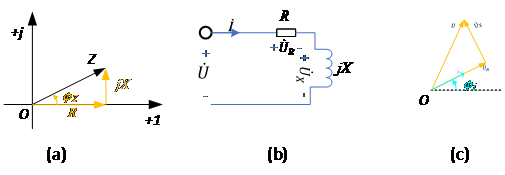
根据阻抗表示欧姆定律有
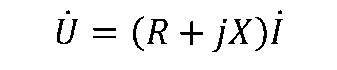
上式表明通过电阻和电抗的是同一电流,等效电路使用两个电路元件串联表示,一为电阻元件R(表示实部),另一元件为储能元件(电感或电容),但要根据电抗的性质来定。
当X>0(φZ>0)时,称为感性电抗,可用等效电感Leq的感抗替代,即
当X<0(φZ<0)时,称为容性电抗,可用等效电感Ceq的容抗替代,即

02正弦稳态电路的功率
有功功率P(平均功率)定义为
它是瞬时功率不可逆部分的恒定分量,也是其变动部分的振幅,它是衡量一端口实际所吸收的功率,其单位用W(瓦)表示。
无功功率Q定义为
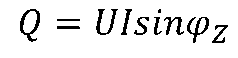
它是瞬时功率可逆部分的振幅,是衡量由储能元件引起的与外部电路交换的功率,这里“无功”的意思是指这部分能量在往复交换的过程中,没有“消耗”掉。 其单位用var(乏)表示。
视在功率S定义为
S=用户界面
它是满足一端口电路有功功率和无功功率两者的需要时,要求外部提供的功率容量,显然有S≥P和S≥Q,P、Q、及S三者的关系为
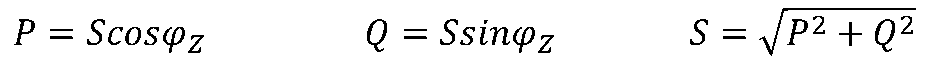
工程上常用视在功率衡量电气设备在额定电压、电流条件下最大的负荷能力,或承载能力(指对外输出有功功率的最大能力)。 视在功率的单位常用V· A(伏安)表示。
上面所用单位W、var和V· A,其量纲相同,目的是区分三种不同的功率。
工程中通常用到功率因数λ的概念,定义为
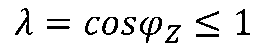
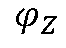
称为功率因数角。 它是衡量传输电能效果的一个非常重要的指标,表示传输系统有功功率所占的比例,即
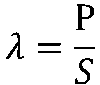
在电路系统中,电感和电容的无功功率有互补作用,工程上认为电感吸收无功功率,而电容发出无功功率。
03复功率
正弦电流电路的瞬时功率等于两个同频率正弦量乘积,其结果是一个非正弦周期量,同时它的频率也不同于电压或电流的频率,所以无法使用相量法讨论。 但是正弦电流电路的有功功率、无功功率和视在功率之间是一个直角三角形关系,可以通过复功率表述。
设一端口的电压相量为
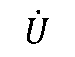
,电流相量为
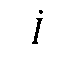
,复功率
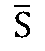
定义为:
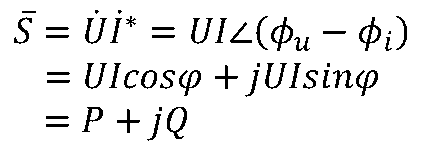
其中
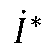
为
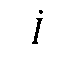
的共轭复数。
对于不含独立源的一端口可以用等效阻抗Z替代,则复功率
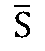
又可以表示为
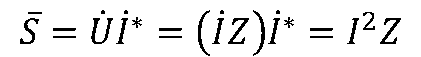
04最大功率传输
含源一端口Ns向终端负载Z传输功率时,当传输的功率较小则不需要计较传输效率,常常需要研究使负载获得最大功率(有功)的条件,如下图所示。
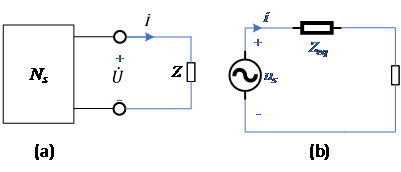
设
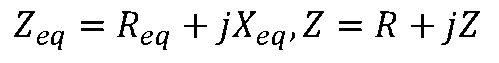
,则负载吸收的有功功率为
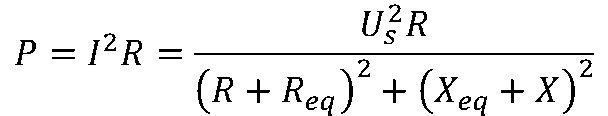
从上式可以看出,负载端获得的功率与一端口等效参数和负载的参数有关,在内部不便变动的情况下,则负载Z必须根据Zeq进行匹配,才可能获得最大功率。 配置条件不同,获得的最大功率也不同。
获得最大功率的条件为:
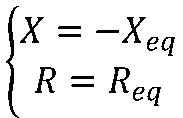
此时获得的最大功率为
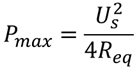
-
利用相量图求解正弦稳态电路2023-03-09 3366
-
电路理论的基础知识之正弦稳态电路的分析2022-01-13 1291
-
正弦交流电路的稳态分析2021-06-19 1583
-
正弦稳态电路的分析学习课件免费下载2020-11-03 947
-
阻抗和导纳及正弦稳态电路的分析和功率的概述2018-07-25 2083
-
电路设计--正弦稳态电路的功率2017-09-14 2088
-
电路设计--正弦稳态电路2017-08-07 1663
-
正弦稳态电路详细解析:正弦稳态电路的定义,正弦稳态电路电路解析2017-05-05 37799
-
正弦稳态电路的功率2010-10-08 543
-
正弦稳态电路的分析与计算2010-04-13 1024
-
非正弦周期信号电路的稳态计算2009-07-27 3783
-
正弦稳态分析2008-12-04 1098
全部0条评论

快来发表一下你的评论吧 !

