线性电路正弦稳态分析方法之相量法

相量法是线性电路正弦稳态分析的一种简易方法。

01 复 数

复数及其运算是应用相量法的基础。

一个复数有多种表示形式。 复数F的代数形式为：

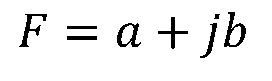
其中为虚单位。 a称为复数F的实部，b成为复数F的虚部。 复数F在复平面上是一个坐标点，常用原点至该点的向量表示，如下图所示。

图1 复数的表现形式

根据上图，可得到复数F的三角形式为：

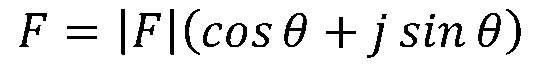
复数F的指数形式或极坐标形式为：

式中| F|为复数的模值，θ为复数的辐角，可以用弧度或度表示。 他们之间的关系为：

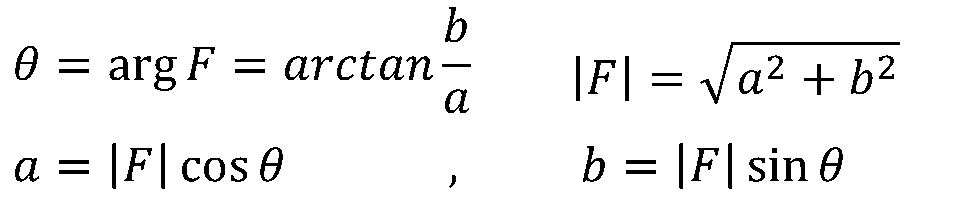
有时候还使用Re[F]=a表示取复数F的实部，Im[F]=b表示F的虚部;

F*表示复数F的共轭复数，即

注：两个实部相等，虚部互为相反数的复数互为共轭复数。

1.1复数加减运算

复数的相加和相减。

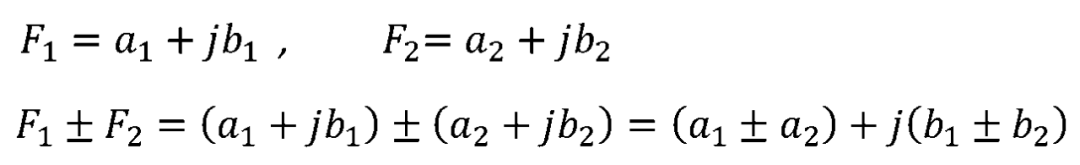
复数的加减运算可以使用平行四边形法在复平面上用向量的相加和相减求得。

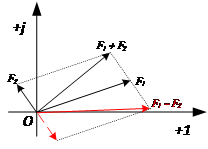
1.2复数的乘除运算

复数相乘使用指数形式较为方便

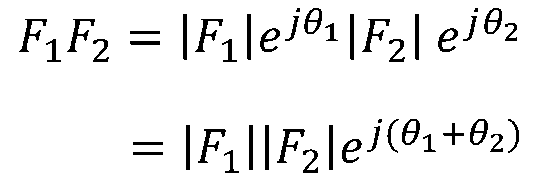
故

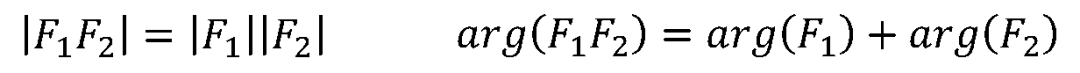
用代数形式表示为：

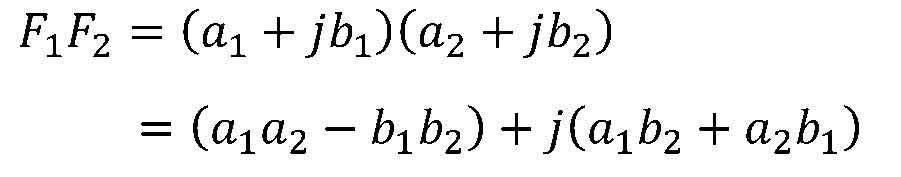
复数相除运算为：

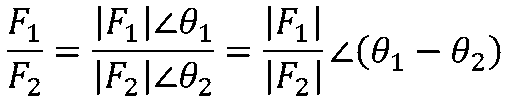
故有

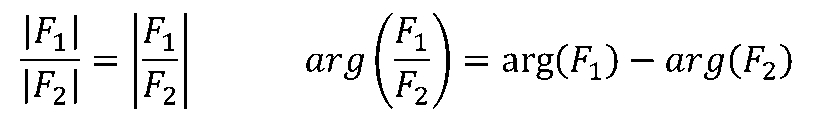
代数形式：

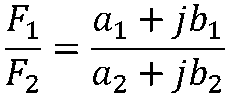
后续可以上下同乘以F2的共轭复数进行有理化运算。 复数乘以共轭复数为实数。

复数乘除运算图解如下图所示：

从上图可以看出：复数乘、除表示为模的放大或缩小，辐角表示为逆时针旋转或顺时针旋转。

复数

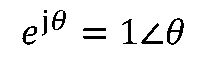
是一个模等于1，辐角为θ的复数。 任意复数
 

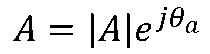
乘以于把复数A逆时针旋转一个角度θ，而A的模不变，故称为旋转因子。

根据欧拉公式，

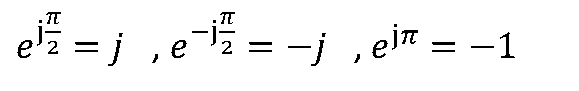
。 因此“±j“和”-1“都可以看成旋转因子。

例如一个复数乘以j等于把该复数在复平面上逆时针旋转π; 要给复数除以j等于把该复数乘以-j，因此等于把它顺时针旋转π/2。

02 正 弦 量

电路中按照正弦规律变化的电压或电流，统称为正弦量。

若在电路中有正弦电流i,指定参考方向下，其数学表达式如下：

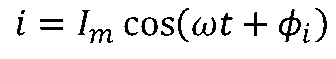
式中的3个常数

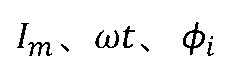
称为正弦量的三要素。

Im称为正弦量的振幅，它是正弦量在整个振荡过程中达到的最大值，也是正弦量的极大值。

随时间变化的角度称为正弦量的相位，或相角。 ω称为正弦量的角频率，它是正弦量的相位随时间变化的角频率，即：

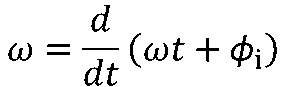
单位为rad/s(弧度/秒)。 它与正弦量的周期和频率f之间的关系为：

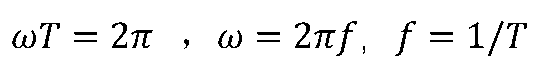
频率f的单位为1/s(1/秒)，称为Hz(赫兹，简称赫)。

ϕi是正弦量在t=0时刻的相位，称为正弦量的初相位(角)，简称初相，即

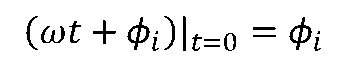
初相的单位用弧度或度表示，通常在主值范围内取值，即|ϕi|≤180°。 初相与计时零点的选择有关。

对于同一电路系统中的许多相关的正弦量，只能相对于一个共同的计时零点确定各自的相位。

正弦量的三要素是正弦量之间进行比较和区分的依据。

正弦量随时间的变化的图形称为正弦波。 下图为正弦电流i的波形图(ϕi>0),横轴可以用时间t或wt(rad)两种方式表示。

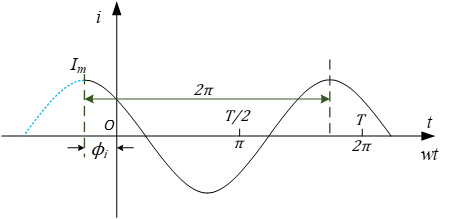
正弦量乘以常数，正弦量的微分、积分，同频正弦量的代数和等运算，其结果仍为一个同频率的正弦量。

工程中常将周期电流或电压在一个周期内产生的平均效应换算为等效的直流量，以衡量和比较周期电流或电压的效应，这一等效的直流量就称为周期量的有效值，用相应大写字母表示。

如周期量i的有效值I定义如下：

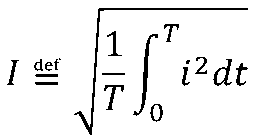
即周期量的有效值等于其瞬时值的平方在一个周期内积分的平均值的平方根，因此有效值也称均方根值。

有效值和峰值的关系：

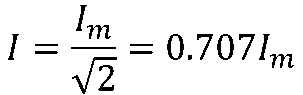
两个同频正弦量的相位差等于它们相位相减的结果。

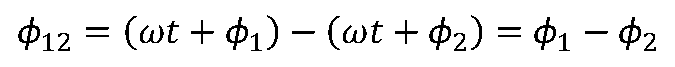
同频正弦量的相位差等于初相位之差，是一个与时间无关的常数。 电路中常用“超前”和“滞后”来表示两个正弦量之间的相位关系。

当ϕ12>0时，称为1超前2，或2滞后于1; 当ϕ12=0时，称为1和2同相;|ϕ12|=π/2时，称1和2相交;|ϕ12|=π时，称1和2反相。

03 相量法的基础

相量法是分析正弦电路稳定状态的一种简易方法。

根据电路定律VCR、KCL和KVL，编写含有储能元件的线性非时变电路的电路方程，如下所示。

 

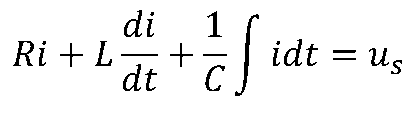
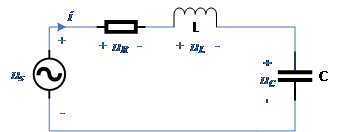
当us为正弦量时，上述方程中的电流i的特解(响应的强制分量)一定是与us同一频率的正弦量。 即线性非时变电路在正弦电源激励下，各支路电压、电流的特解都是与激励同频率的正弦量，当电路中存在有多个同频率的正弦激励时，该结论同样成立。

工程中将电路的这一特解状态称为正弦电路的稳定状态，简称正弦稳态。 电路处于正弦稳态时，同频率的各正弦量之间，仅在有效值、初相上存在“差异和联系”。

电路中正弦电压us和正弦电流i对应的向量可以表示为：

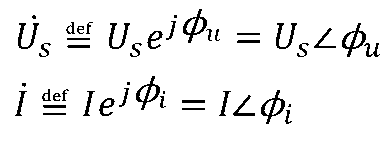
即正弦量的对应相量是一个复数，它的模为正弦量的有效值，它的辐角为正弦量的初相。

相量在复平面上表示的图形称为相量图，如下图所示。

电路中有时也用正弦量的振幅表示相量的模，称为振幅相量。

04 电路定律的相量形式

用相量通过复数形式的电路方程描述电路的基本定律VCR(电压、电流和电阻关系)、KCL(基尔霍夫电流定律)和KVL(基尔霍夫电压定律)，称为电路定律的相量形式。

注：电路的运行规则由电路的结构和元件的特性共同决定，KCL和KVL描述电路结构，VCR描述元件特性。

KCL的相量形式：

对电路中任一节点有：

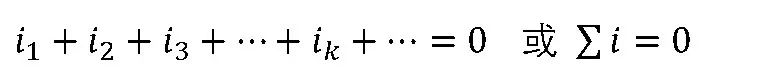
当式中的电流全部都是同频率的正弦量时，则可变换为相量形式为：

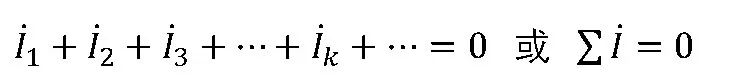
即任一节点上同频率的正弦电流的对应相量的代数和为零。

KVL的相量形式：

对电路中任一回路有：

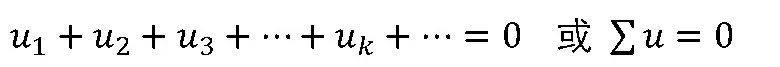
即任一结点上同频的正弦电流的对应相量的代数和为零。

当式中的电压全都是同频的正弦量时，可变换称相量形式为：

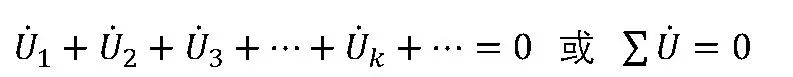
即任一回路中同频的正弦电压的对应相量的代数和为零。

电阻、电感和电容元件的VCR的相量形式：当有正弦电流

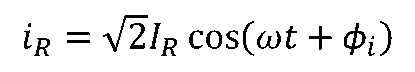
通过时，根据欧姆定律，电压-电流的时域关系为
 

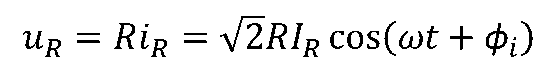
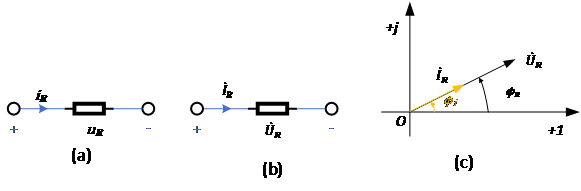
说明电阻上的电压、电流都是同频的正弦量。 令电压相量为

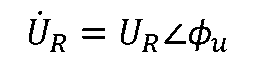
，则相量形式有

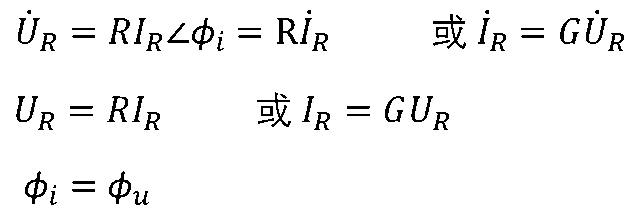
他们的有效值依然符合欧姆定律，辐角相等，即电压电流同相。

若是电感电路中，有正弦电流

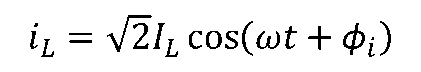
通过时，根据电感的电压-电流的时域关系有

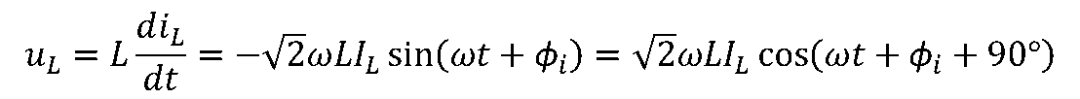
说明电感L上的电压、电流为同频正弦量。 令电压相量为

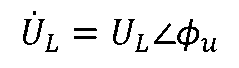
，uL的表达式变换后的相量形式为

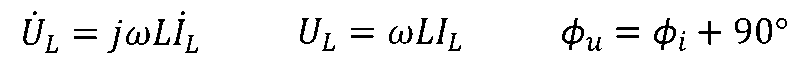
电压、电流有效值之间的关系类似于欧姆定律，但与角频率ω有关，其中与频率成正比的ωL具有与电阻相同的量纲[Ω]，称为感抗， -1/ωL称为感纳;

电感L上的电压将跟随频率变化，当ω=0时(直流), ωL=0,uL=0，电感相当于短路; 当ω=∞时,
ωLà∞,i=0，电感相当于k开路，在相位上电压超前电流90°。

对于电容电路而言，有和电感相似的特性，只不过刚好相反。

其结论如下：

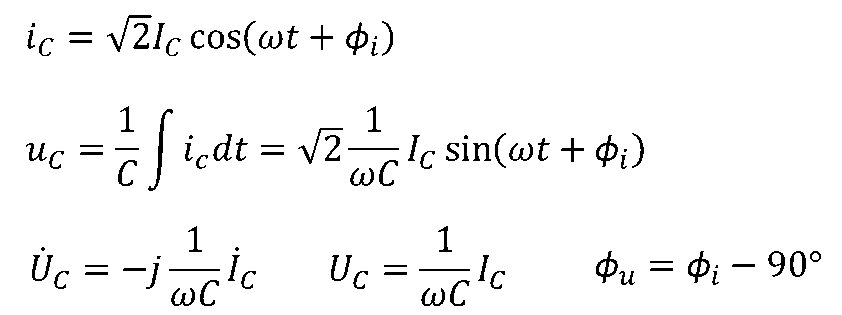
电压、电流有效值之间的关系类似于欧姆定律，但与角频率ω有关，其中与频率成正比的-1/ωC具有与电阻相同的量纲[Ω]，称为容抗，ωC称为容纳;

电容C上的电压将跟随频率变化，当ω=0时(直流),1/ωC =∞,iC=0，电容相当于开路; 当ω=∞时,1/ωC à0,
uL=0，电容相当于短路，在相位上电压滞后电流90°。