动态电路的方程及其初始条件 一阶电路的时域分析

01 动态电路的方程及其初始条件

电容元件、电感元件这种电压、电流的约束关系是通过导数(或积分)表示的，称为动态元件，或称为储能元件。 含有动态元件的电路被称为动态电路。 动态电路的一个特征是当电路的结构或者元件的参数发生变化时，可改变电路的工作状态，这种转变往往需要一个过程，在工程上称为过渡过程。 上述电路结构或参数变化引起的电路变化统称为“换路”，并认为换路是在t=0时刻进行的。 为了叙述方便，把换路前的最终时刻记为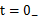把换路后的最初时刻记为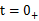换路经历的时间为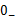到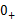。 分析动态电路的过渡过程的方法之一是：根据KCL、KVL和支路的VCR建立描述电路的方程，这类方程是以时间为自变量的线性常微分方程，然后求解常微分方程，从而得到电路所求变量(电压或电流)。 此类方法称为经典法，这是一种在时间域中进行的分析方法。

对于线性电容，在任意时刻t时，它的电荷、电压与电流的关系为：

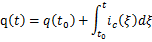
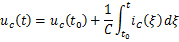
式中q,uc和ic分别为电容的电荷、电压和电流。 令，则得

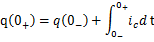
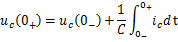
如果在换路前后，即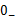到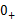的瞬间，电流为有限值，上式中右方的积分项将为零，此时电容上的电荷和电压就不会发生跃变，即

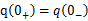
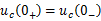
即在换路的瞬间，带电电容可视为一个电压值为U0的电压源。 同理，对于不带电荷的电容，在换路瞬间电容相当于短路。

线性电感的磁通链、电流和电压的关系为

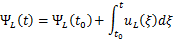
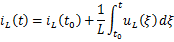
令

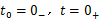
，则得

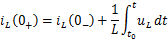
如果在换路前后，即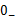到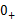

的瞬间，电压为有限值，上式中右方的积分项将为零，此时电感中的磁通链和电流不发生跃变，即

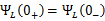
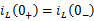
电感在换路瞬间可视为一个电流值为的电流源。 同理对于电流为零的电感，此电感在换路瞬间相当于开路。

02 一阶电路零输入响应

动态电路中无外施激励电源，仅由动态元件初始储能所产生的响应，称为动态电路的零输入响应。

03 一阶电路零状态响应

零状态响应就是电路在零初始状态下(动态元件初始储能为零)由外施激励所引起的响应。

04 一阶电路的全响应

一个非零初始状态的一阶电路受到激励时，电路的响应称为一阶电路的全响应。 在下图所示电路为已充电的电容经过电阻接到直流电压源Us。 设电容原有电压uc=U0，开关闭合后，根据KVL有

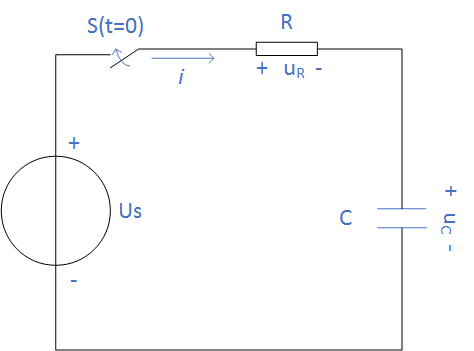
即有

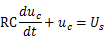
初始条件

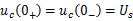
方程的通解

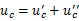
取换路后达到稳定状态的电容电压为特解，则

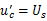
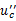
为上述微分方程对应的齐次方程的通解

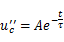
其中

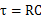
为电路的时间常数，所以有

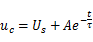
得积分常数为

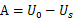
所以电容电压

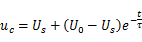
这就是电容电压在t>0时的全响应。 上式可以改写为

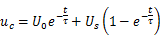
即全响应 =(零输入响应)+(零状态响应)全响应 = (强制分量)+(自由分量)全响应 =
(稳态分量)+(瞬态分量)全响应是由初始值、特解和时间常数三个要素决定的。

在直流电源激励下，若初始值为，特解为稳态解，时间常数为τ，则全响应

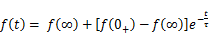
只需要知道这三个要素，则可以根据上式直接写出直流激励下一阶电路的全响应，这种方法称为三要素法。 如果电路中仅含一个储能元件(L或C)，电路的其他部分有电阻和独立电源或受控源连接而成，这种电路仍是一阶电路。 求解这类电路时，可以把储能元件以外的部分，使用戴维宁定理或者诺顿定理进行等效变换，然后求得储能元件上的电压和电流。 如果还要求其他支路上的电压和电流，则可以按照变换前的原电路进行。