线性电路的基本定理

01 叠加定理

作为线性系统(包含线性电路)最基本的性质—线性性质，它包含可加性与齐次性两方面。 叠加定理是可加性的反应，它是线性电路的一个重要定理。 可加性的概念可以说是贯穿于电路分析之中，并在叠加定理中得到直接应用。

叠加定理可表述为：在线性电阻电路中，某处电压或电流都是电路中某个独立电源单独作用时，在该处分别产生的电压或电流的叠加。

叠加定理在线性电路的分析中起着非常重要的作用，它是分析线性电路的基础。

使用叠加定理应注意：

1、 叠加定理适用于线性电路，不适用于非线性电路;

2、在叠加的各分路电路中，不作用的电压源置零，在电压源处用短路替代; 不作用的电流源置零，在电流源处用开路代替。 电路中所有电阻都不予更动，受控源则保留在各分电路中。

3、 叠加时各分电路中的电压和电流的参考方向可以取为与原电路中的相同。 取代数和时，应注意各分量前的“+”、“-”号;

4、 原电路的功劳不等于按各分电路计算所得功率的叠加，这是因为功率是电压和电流的乘积，与激励不成线性关系。

齐次定理：在线性电路中，当所有激励(电压源和电流源)都是同增大或者缩小N倍(N为实常数)时，响应(电压和电流)也将同样增大或缩小N倍。

注意：激励是指独立电源，并且必须全部同时增大或者缩小N倍，否则不适用。

02 替代定理

替代定理是一个应用范围广泛的定理，它不仅适用于线性电路，也适用于非线性电路。 它时常用来对电路进行简化，从而使电路易于分析或计算。

替代定理：在电路中如已求得NA与NB两个一端口网络连接端口的电压up与电流ip，那么就可用一个us=up的电压源或一个is=ip的电流源来代替其中的一个网络，而使另一个网络的内部电压、电流均保持不变。

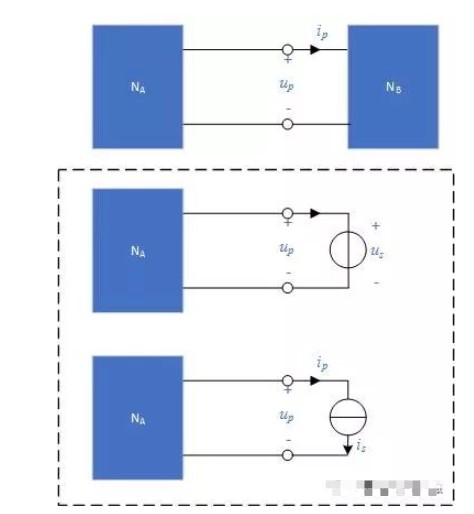
如果NB中有NA中的受控源的控制量，NB被替代后将无法表达这种控制关系，这时NB就不可以被替代。

03戴维宁定理和诺顿定理

戴维宁定理：一个含独立电源、线性电阻和受控源的一端口，对外电路来说，可以用一个电压源和电阻的串联组合等效变换，此电压源的激励电压等于一端口的开路电压，电阻等于一端口内全部独立电源置零后的输入电阻。

诺顿定理：一个含独立电源、线性电阻和受控源的一端口，对外电路来说，可以用一个电流源和电阻的并联组合等效置换，电流源的激励电流等于端口的短路电流，电阻等于一端口全部独立元置零后的输入电阻。

注意：这里受控源智能受端口内部的电压、电流的控制; 同时，端口内的电压、电流也不能是外电路中受控源的控制量。

04 最大功率传输定理

在通讯、测量等系统中首要问题是如何从给定的信号源(产生通讯信号或者测量信号的“源”)取得尽可能大的信号功率。 由于此时传输的功率不大，因此效率问题并不是第一位考虑的问题。

这里就不推导了，直接给出结论!

当负载电阻RL=RS(等效内电阻)时，负载可以获得最大功率，这种情况称为RL和RS匹配。

05特勒根定理

特勒根定理是电路理论中对集总电路普遍适用的基本定理; 就这个意义上，它与基尔霍夫定律等价。

特勒根定理1：对于一个具有n个结点和b条支路的电路，假设各支路电流和支路电压取关联参考方向，并令(i1,i2,…,ib)、(u1,u2,…,ub)分别和b条支路的电流和电压，则对任何时间t，有

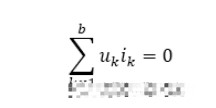
特勒根定理2：如果有两个具有n个结点和b条支路的电路，他们具有相同的图，但由内容不同的支路构成。 假设各支路电压和电流都取关联参考方向，并分别用

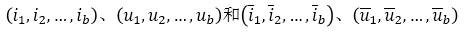
表示两电路中b条支路的电流和电压，则在任何时间t，有

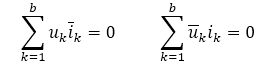
注意：定理2不能用功率守恒解释，它仅仅是对两个具有相同拓扑的电路中，一个电路的支路电压和另一个电路的支路电流，或者可以是同一电路在不同时刻的相应支路电压和支路电流必须遵循的数学关系。

由于他仍具有功率之和的形式，所以有时也称为“拟功率定理”。 定理2对支路内容没有任何限制，该定理普遍适用。

06 互易定理

互易定理：对于一个仅含线性电阻且只有一个激励的电路，在保持电路将独立电源置零后电路拓扑结构不变的条件下，激励和响应互换位置后，响应与激励的比值保持不变。

上述互换后拓扑结构不变有三种可能，这构成了互易定理的三种形式。

下图(1)(2)示出第一种激励和响应互换位置的形式，(3)为把(1)(2)中的独立源归零后的拓扑结构。

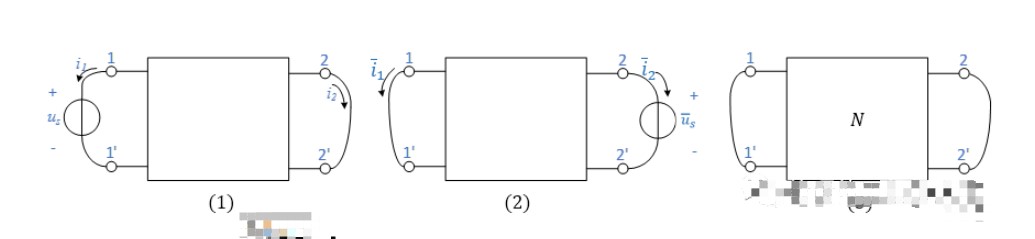
根据互易定理，应有

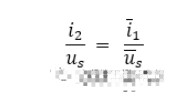
当

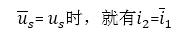
下图(1)(2)示出第二种激励和响应互换位置的形式，(3)为把(1)(2)中的独立源归零后的拓扑结构。

根据互易定理，有

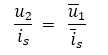
可见，响应与激励的比值不变，当

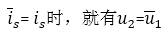
下图(1)(2)示出第三种激励和响应互换位置的形式，(3)为把(1)(2)中的独立源归零后的拓扑结构。

根据互易定理，有

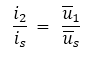
当

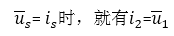
最后需要强调的是，为使互易定理得以使用，方框内部N的(b-2)条支路的电压、电流必须满足下列关系

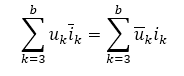
这一关系是判断网络是否可互易的条件。 能满足此关系的网络称为可互易网络，其元件称为可互易元件。 受控源的控制是有方向性的，所以受控源就不是可互易的，具有受控源的电路也不是可互易网络。