

利用相量图求解正弦稳态电路
描述
正弦稳态电路有时利用相量图求解比直接计算简单。
例:图1电路中,已知U=100V,R2=6.5Ω,R=20Ω,当调节触点C使得Rac=4Ω时,电压表读数最小,为30V,求复阻抗Z。
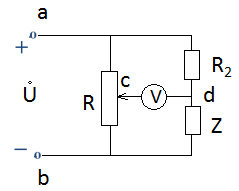
图1 待求电路
分析:注意此题不是电桥,电压表所在支路如果接电流表,或电阻,该电路是电桥。 但此时接的是理想电压表,其内阻无穷大。 电压表的作用是测量cd 两点间的电压。 此题利用相量图法辅助分析比较直观且易于理解。
以并联电压为参考相量画相量图,如图2所示。 假设Z为感性负载Z=R1+jX,Z所在支路阻抗角为ϕ,电压表读数为
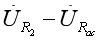
的模值。 当触点C滑动时,
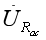
在水平线上移动。 显然当
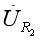
末端与
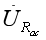
末端连线为垂直线时,该线条(图中虚线)长度最短。 而此虚线的长度即为伏特表所测量的电压值。
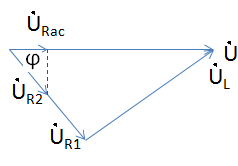
图2 相量图
根据题意,
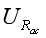
=20V,虚线长度为30V,则根据勾股定理:
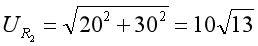
在。
可得复阻抗支路电流I2:
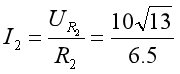
而由图2中,虚线所示的小直角三角形,有:
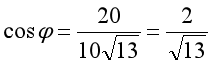
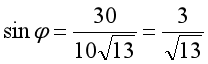
图2中,
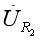
和
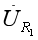
的方向与该支路电流I2的方向一致,并与
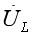
的方向垂直。 所以图2中蓝色的大三角形也是直角三角形,故有:
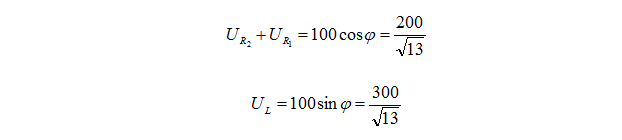
根据欧姆定理,可得
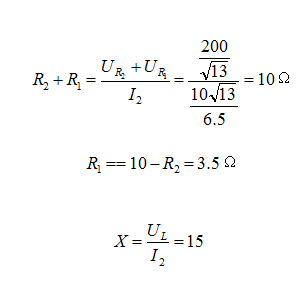
因为Z也可能为容性负载,所以Z=3.5+j15 或Z=3.5-j15Ω。 由此得解。
此题中当Z为纯电抗时,计算相对更为简单。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
正弦交流电路的稳态分析相量法2023-10-28 3951
-
线性电路正弦稳态分析方法之相量法2023-03-09 9741
-
电路理论的基础知识之正弦稳态电路的分析2022-01-13 1291
-
正弦交流电路的稳态分析2021-06-19 1583
-
正弦稳态电路的分析学习课件免费下载2020-11-03 947
-
正弦稳态电路的相量模型的详细资料说明2019-04-15 1221
-
电路设计--正弦稳态电路2017-08-07 1663
-
正弦稳态电路详细解析:正弦稳态电路的定义,正弦稳态电路电路解析2017-05-05 37797
-
正弦稳态电路的功率2010-10-08 543
-
正弦稳态电路的分析与计算2010-04-13 1022
-
非正弦周期信号电路的稳态计算2009-07-27 3783
-
正弦稳态分析2008-12-04 1098
-
正弦稳态交流电路相量的研究2008-09-22 25242
全部0条评论

快来发表一下你的评论吧 !

