

如何精准计算出书里每张纸的厚度?
描述
给你一本书,你能用普通的刻度尺,量出一张纸的厚度吗?
答案是肯定的!我想读者都已经想到了到了。谜底是,量出全书的厚度(如果书很薄,可以把相同的书叠几本!),然后除以全书纸的张数,即得每张纸的厚度。
以《辞海》缩印本(1980年8月版)为例,该书除封面外厚60毫米,全书共2256页,计1128张纸,那么每张纸厚约
x=60/1128=0.0532(毫米)
上述方法可以用于类似的场合。
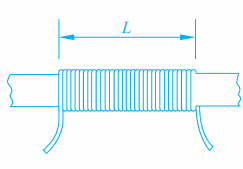
例如,为了测出细漆包线的直径大小,可以采用绕线的办法,在一根铅笔上,紧密地绕上n圈,测量出这n圈漆包线在铅笔上所占位置的长L,则该漆包线的直径d,显然应该满足
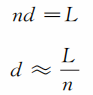
然而,尽管很多人都懂得应该这样去做,但并不一定所有的人都知道这样做的科学原理。
仍以测量《辞海》的书页为例,实际上我们很难找到书中哪一页纸的厚度恰好等于0.0532毫米,所有1128张纸都有它们各自的厚度(单位:毫米)
a1,a2,a3,…,a1128
只是这1128个数的总和是一个常量,即
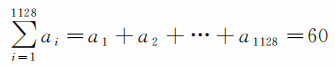
而0.0532毫米,则是这1128个数的平均值。现在需要证明的是:对于量x的n个观测值a1,a2,…,an,它们的平均值
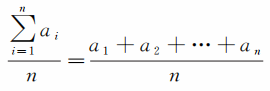
是所要测定的量x的最理想取值。式中求和符号表示从1累加到n。
事实上,最理想的取值x,应当使它与n个观察值的差的总和为最小。但考虑到差(x-ai)(i=1,2,…,n)可能有正有负,如果直接把它们相加,势必使某些差的值相抵消,影响了偏离的真实性,这显然是不合理的。
于是,人们想到了用(x-ai)的2次方来替代相应的差。这样一来,最理想的取值x应当使函数
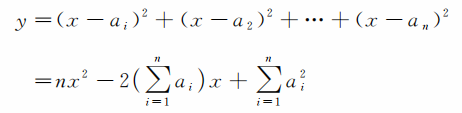
取极小值。这是关于x的二次函数,易知当时y取极小。这就是为什么平均值可以看成是观测量最理想取值的道理。
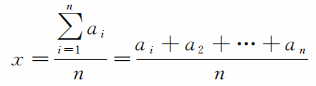
同样的原理可以用于二维的情形,只是计算稍微复杂一些,我们将要得到的结果在数学上非常有名,叫作最小二乘法。它是德国数学家高斯于1795年创立的,那时他年仅18岁!现在假定我们观察到n个经验点:
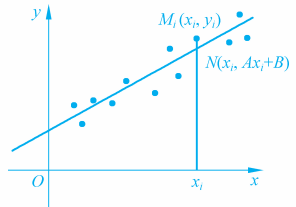
(xi,yi),(x2,y2),…,(xn,yn)
如果我们认定这n个经验点Mi(i=1,2,…,n)是对直线y=Ax+B上的点在观测时的误差。那么,这些经验点Mi(xi,yi)与直线上相应点N(xi,Axi+B)之间的以下量

应当取极小值。“最小二乘法”的名称,大约就是由此而来!
函数y显然可以写成A的二次函数
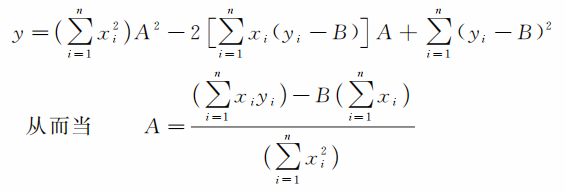
时取极小值。整理得
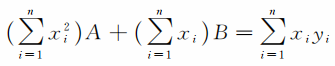
同理,函数y又可以写成B的二次函数,而当这一函数取极小值时,又得
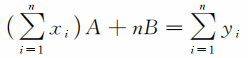
这样,由线性方程组
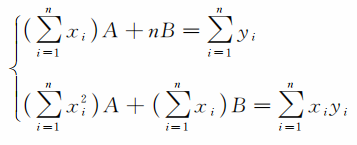
便可以确定参数A、B的值。从而得到一条最逼近n个经验点Mi(i=1,2,…,n)的直线
y=Ax+B
最小二乘法在科学上有许多妙用。
下面是一个实例,数学工具帮助历史学家解开了一个千古之谜!
传说古日本有一个邪马台国。239年,邪马台国女王卑弥呼曾经派遣使臣前往当时魏国的京都洛阳,向魏明帝(曹操的孙子)进贡物品。魏明帝赐卑弥呼为“亲魏倭王”,并赏给黄金、丝绸等大批物资。
这个历史事件,在经历了近两千年的漫长岁月后,在人们的记忆中渐渐淡薄,连邪马台国位于日本岛的何方也成了不解之谜!
东京大学有位历史学教授平山朝治,不仅精通历史,而且擅长数学。一天,平山教授正专心翻阅中国古籍史书《三国志》,突然一篇《魏志·倭》落入他的视野。文中记述了当时魏国使者前往倭国的实际行程。平山对邪马台国的奥秘发生了浓厚的兴趣。他把文章细读了一遍,见文中写道:
“从郡至倭,循海岸水行,历韩国,乍东乍南,到其北岸狗邪韩国,七千余里,始渡一海,千余里至对马国。……又南渡一海千余里,……至一大国,……又渡一海,千余里至末卢国,……东南陆行五百里,到伊都国,……东南至奴国百里,……东行至不弥国百里,……南至投马国,水行二十日,……南至邪马壹国,女王之所都,……可七万余户。”
然而,当平山先生读完全文时,原先热乎乎的心,凉了半截!
原来《魏志·倭》中的“里”,是个谜中之谜!这种怀疑不能说没有道理。古代的长度单位显然是不同于今的。就好像《三国演义》里描写刘备身高7.5尺,张飞身高8尺,关云长身高9尺。按现在换算,他们的高度堪称世界之最。..。..。
又如《水浒》中矮得出奇的武大,书中写他身高5尺,这在现在已是中等个儿,所以文中的“里”就更值得打个问号了!
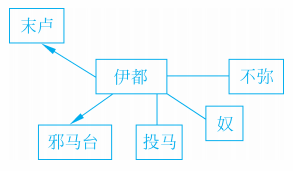
不过,平山先生并没有因此灰心丧气。他从《魏志·倭》的字里行间的差异,分析出了伊都国应当是使者的大本营。又“对马国”和“一大国”,被令人信服地判明就是现今的对马岛和壹歧岛。这样,平山就使自己的所有数据,有了一个可被信赖的参照点。从而使得他能够运用科学的最小二乘法,找到了魏时的里与今天千米之间的函数关系
y=-9.90+0.0919x
由此判定,伊都国即当今日本国本州岛的福岗县。不过,接下去情况似乎有点不妙!因为最后推出邪马台国竟坐落在九州岛的荒凉山区。这是不可思议的!连平山本人也怀疑这样的结论!昔日有7万户的繁华国度,今天不可能荒无人迹!
经过反复研究,推测使者实际上走的并非是一条直线,而是一条弧线。经修正后,平山教授得出了以下结论:“古邪马台国中心,位于现日本国福冈县的久留米。”
审核编辑 :李倩
-
如何计算出ADE7880的功率因子?2023-12-26 1168
-
请问TAS5805M如何将计算出的系数转换为tas5805对应数据?2024-09-30 208
-
STM32F1 xcube cryptolib ECDSA计算出来的摘要值和外部验证工具计算出来的签名值对不上怎么解决?2025-03-07 358
-
请问如何计算出ADE7880的功率因子?2018-08-22 1641
-
请问信噪比是怎么计算出来的2018-09-13 6046
-
这个电阻2.2如何计算出来的,oa ob 的最大电流是多少?2018-10-14 2495
-
请问普通的光耦能否计算出比较精准的位移和速度?2019-01-17 2445
-
PWM的占空比是怎么计算出来的?2020-08-04 3997
-
mbedtls计算出与SDK不同的cmac签名是怎么回事?2023-02-28 515
-
malloc库如何计算出正确的堆大小?2023-03-27 370
-
相对式编码器要怎么计算出转动的角度?2023-10-12 397
-
读出绝对值编码器的值以后如何计算出角度值?2023-10-13 476
-
电路是计算出来的2016-10-10 483
-
教你快速计算出DCDC电感参数2022-01-17 1222
-
dd马达偏差量怎么计算出来的2024-07-11 1749
全部0条评论

快来发表一下你的评论吧 !

