

信号完整性的知识点
描述
时域和频域
对时域和频域最直观的感受可以从波形上看出来。下图<1>是一个1MHz的方波时域波形,下图<2>是此方波的频域波形。时域图的横轴坐标是时间(us),纵轴坐标是信号电压幅度(V)。频域图的横轴坐标是频率(xHz),纵轴坐标是信号幅度(dB)。它们是使用LTspice仿真软件得到。
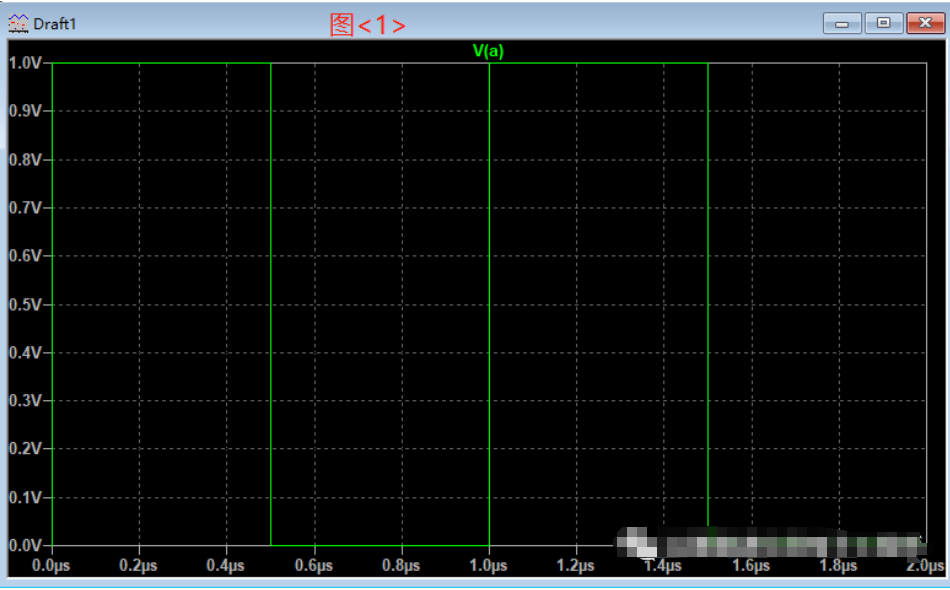
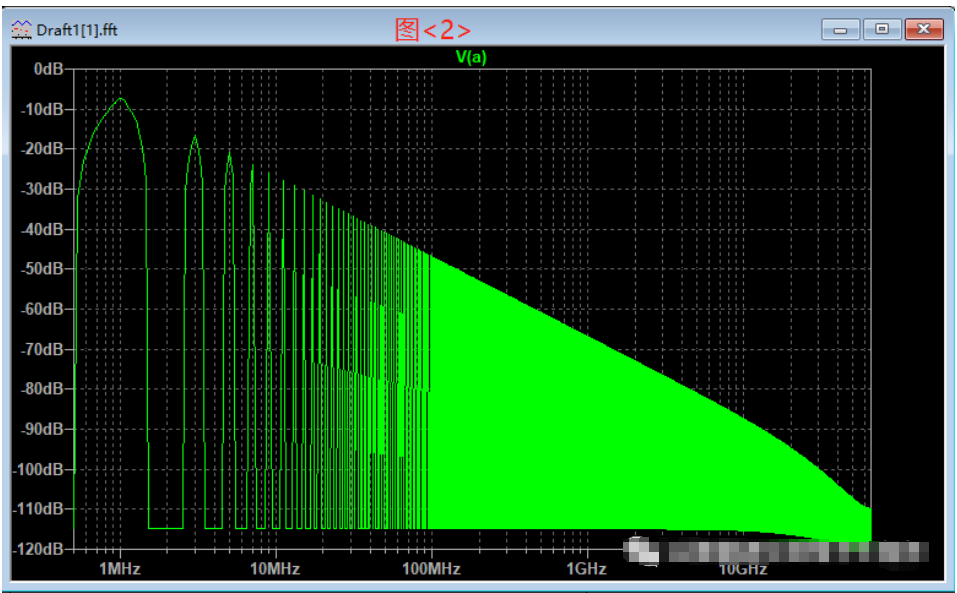
时域就像我们的人生,从出生开始向前延伸,没有机会重来。信号在时域中也是一直向前,从波形上看就是沿着时间轴,显示每时每刻信号的电压和电流的样子,它是以时间为基准的。频域在我们真实世界中是不存在的,它是以信号的频率为基准,显示信号包含的各个频率点对应的电压和电流的样子。时域的信号经过数学计算得到的就是频域信号,有三种方法实现信号从时域到频域的转变(傅里叶积分、离散傅里叶变换和快速傅里叶变化)。
任何波形都是正弦波的集合
在频域中唯一存在的波形就是正弦波。换句话说时域中的任何波形都是由频域中的一系列正弦波组合而成。这些正弦波分量都有各自相关的频率、幅度和相位。把所有这些频率值和幅度值的集合称为波形的频谱。频谱中的正弦波频率是时域中信号频率的整数倍。第一个正弦波频率称为一次谐波,第二个正弦波分量称为二次谐波,依次类推。而零次谐波就是直流分量值。
例如上图<2>,假设此理想方波的幅度是1V。它的所有偶次谐波幅度都为0,只存在奇次谐波。奇次谐波的幅度为
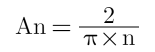
An: n次谐波的幅度
n:谐波数
要想从频谱信号中得到它的时域波形,只需要将频域中所有频率的信号转换成时域中正弦波的集合,并且将这些正弦波全部叠加即可。图3是包含10谐波的方波,图4是包含100次谐波的方波。可以看出包含的谐波分量越多,方波上升沿和下降沿越陡峭,方波越完整。
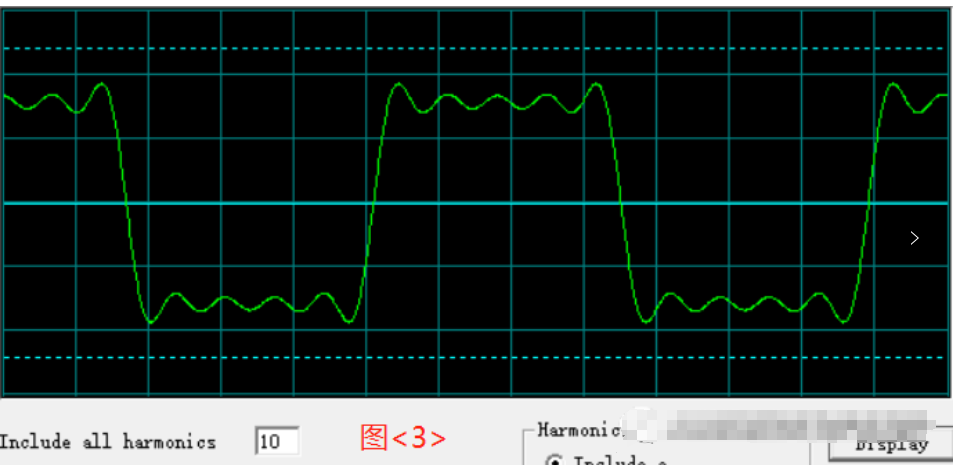
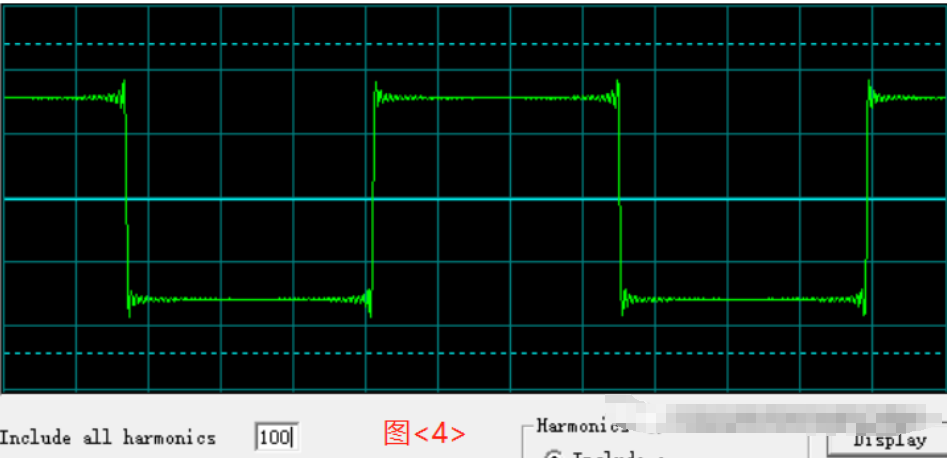
问题来了,一个波形包含多少谐波分量就足够了?是10次、100次、还是越多越好?这就引入了带宽的概念。
带宽
所谓带宽是指从一个信号的频域角度看,为了充分表现时域波形的特征,在其频谱中需要包含的频率范围,即有效频率范围。在此范围之外的频率分量可以不用考虑。
通常所谓有效是指,实际信号的谐波幅度高于相同频率的理想方波中相应谐波幅度70%的频率点。高于此点的谐波幅度会很低,对恢复信号时域波形已经没有多少贡献,可以忽略。
有一个关于信号上升时间和带宽的经验法则是:
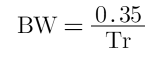
BW是信号带宽
Tr是信号的上升时间
结合前一篇文章提到的大多数信号的上升时间是其周期的十分之一,可以粗滤估算信号带宽。
有一种情况是:如果实际电路的阻抗控制不好,导致信号发生振铃等现象,此时这个信号的带宽会比没有振铃现象的信号带宽要大。在频谱上会看到,振铃频率点对应的频谱频率处会有尖峰幅值出现。因此当在EMC实验中出现某些频率点超标,而整个电路中又没有对应频率的信号时,检查数字信号是否有振铃,也是一个方向。因为电路中的振铃可能会使高频分量的幅度增加,进而导致辐射幅度增加。
第二种情况是:同样频率的正弦波和方波带宽也不相同。方波的带宽更大,这是因为信号带宽是由信号上升时间决定,而不是由频率决定。上升时间越短,信号包含的高频谐波越多,信号带宽越宽,EMI噪声越大。
在EMI对策中,有个粗陋的经验值(仅仅是经验值),数字信号的滤波电路截止频率要保证25~35次以内的谐波都要存在,以外的谐波滤除。
-
把信号完整性设计落到实处2024-08-30 1082
-
高速电路设计常见的知识点2023-02-13 2127
-
何为信号完整性?信号完整性包含哪些2021-12-30 2769
-
信号完整性为什么写电源完整性?2021-11-15 1448
-
信号完整性与电源完整性的仿真2021-09-29 1511
-
信号完整性中需要掌握的基础知识点资料下载2021-03-31 1702
-
信号完整性基础知识2019-04-11 2275
-
关于信号完整性的31个知识点汇总2018-06-05 1362
-
我们为什么重视系统化信号完整性设计方法(于博士信号完整性)2017-06-23 3097
-
于博士《信号完整性--系统化设计方法及案例分析》高级研修班2016-05-05 3786
-
信号完整性分析基础知识2016-01-06 777
-
信号完整性与电源完整性仿真分析2011-11-30 2000
-
什么是信号完整性2009-06-30 5711
全部0条评论

快来发表一下你的评论吧 !

