

如何列写自控元件伺服电动机传递函数
工业控制
描述
如何列写自控元件伺服电动机传递函数
电枢控制直流伺服电动机:
角速度与直流电压之间传递函数:
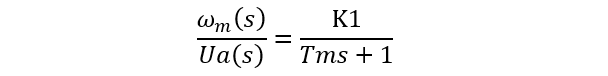
角速度与角度之前传递函数:
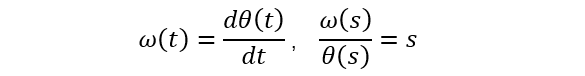
因此,可求出角度与直流电压之间传递函数:
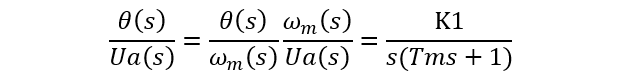
角速度与扰动转矩之间传递函数:
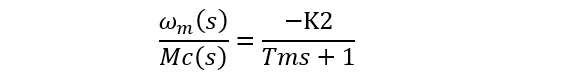
两相交流伺服电动机:
两相交流伺服电动机由互相垂直的两相定子线圈和一个转子组成。定子线圈的一相是激磁绕组,另一相是控制绕组。
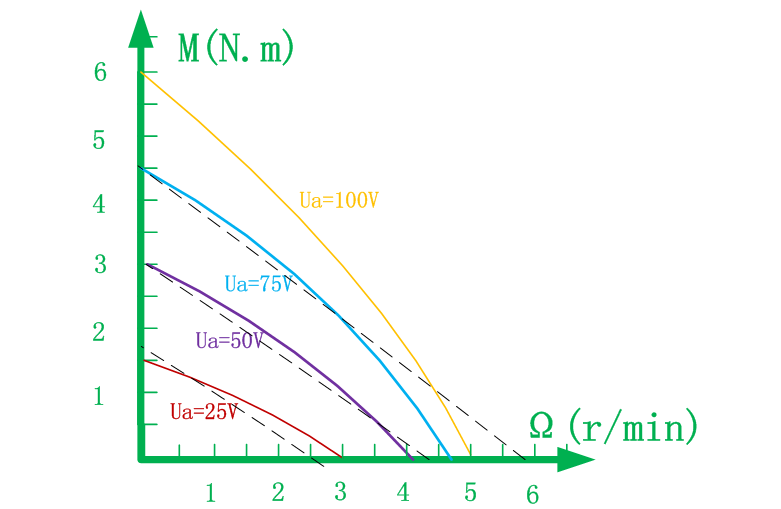
两相伺服电动机转矩-转速特性为负斜率关系,且非线性。上图是电机特性曲线图;
通常反馈角速度值都比较小,可以在低速段对特性曲线进行线性化,以方便数学建模。线性化参考斜率通常选择额定电压一半值对应的曲线进行线性化。图中参考Ua=50V曲线为线性化曲线。线性化方程可表示为:
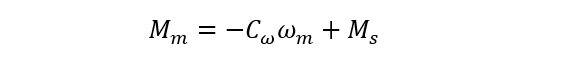
Mm是输出转矩,Ms是堵转转矩,Cω=dMm/dω称为阻尼系数,转速越大,输出转矩越小;
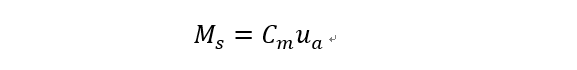
输入电压越大,堵转扭矩越大;参数Cm可用额定电压E时的堵转转矩Mse进行计算:
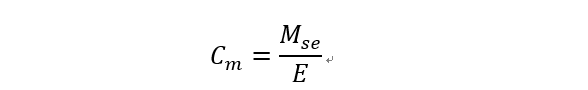
根据叠加原理,负载转矩是扰动输入,控制系统的输出方程可以分别给定输入和扰动输入两种情况下的输出,再应用叠加原理进行叠加求和;在不考虑负载转矩情况下,计算给定输入电压Ua作用系统是系统的输出,电动机输出转矩Mm用来驱动负载并克服粘性摩擦力;列写转矩动态平衡方程:
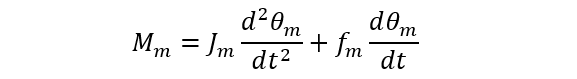
式中,θm是电动机转子角位移,Jm和fm分别是折算到电动机上的总转动惯量和总粘性摩擦系数;
消掉中间变量Mm和Ms,把ω=dθ/dt带入上式中,整理后的微分方程为:
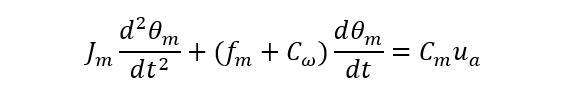
在零初始条件下求拉氏变换:
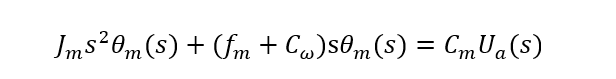
求得两相伺服电动机的传递函数为:
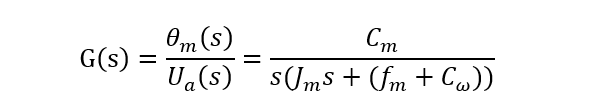
把传递函数化为标准型中的因子形式:
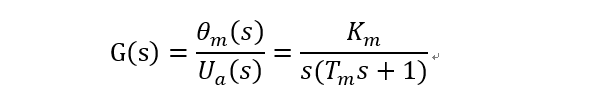
式中,Km=Cm/(fm+Cω)是电动机传递系数,Tm=Jm/(fm+Cω)是电动机时间常数。
由于ω(s)=sθ(s),则上式也可以表示成角速度与电压之间的传递函数:
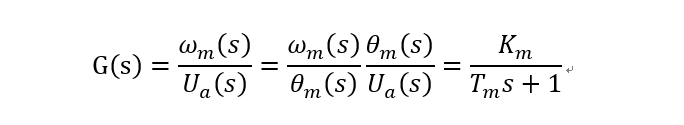
-
传递函数的定义是什么 传递函数的拉氏反变换是什么响应2024-02-01 8447
-
AC伺服电动机的构造和寿命2023-03-20 886
-
如何列写无源网络传递函数2023-03-10 6726
-
三相自控式同步电动机简介2021-09-03 1878
-
自控式同步电动机2021-08-27 1790
-
无刷直流永磁电动机(BLDCM)与自控式永磁同步电动机(PMSM)有何区别2021-08-02 3643
-
永磁交流伺服电动机同直流伺服电动机比较 主要优点有哪些?2021-06-28 2838
-
模拟电路中传递函数的快速列写方法2019-04-20 11314
-
伺服电动机震动有什么危害?2018-12-10 2639
-
传递函数的时域辨识2017-10-26 1615
-
拓扑传递函数的列写2016-08-14 3178
-
电动执行机构传递函数的研究2009-03-17 1106
-
伺服电动机的应用2008-11-19 1587
全部0条评论

快来发表一下你的评论吧 !

