

如何用两种不同的方法列写双容水槽传递函数
描述
如何用两种不同的方法列写双容水槽传递函数
双容水槽
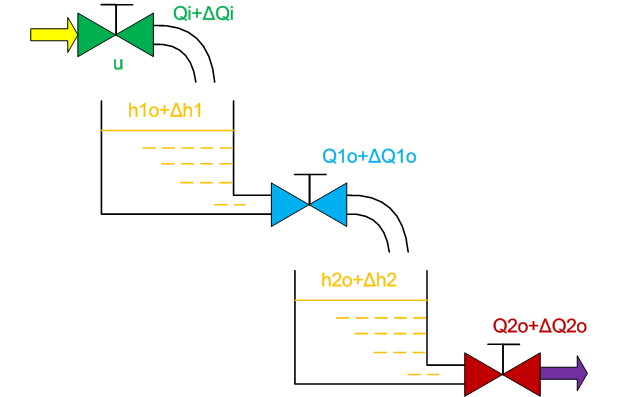
两个串联的单容水槽构成双容水槽,输入量为调节阀1产生的阀门开度变化Δu,延时时间为τ,输出量为第二个水槽的液位增量Δh2;
第二个水槽的数学模型:
设ΔQ1为第二个水槽输入流量,第一个水槽输出流量,ΔA1为第一个水槽横截面积,ΔR1为第一个水槽液阻。设ΔQ2为第二个水槽输出流量,ΔA2为第二个水槽横截面积,ΔR2为第二个水槽液阻。
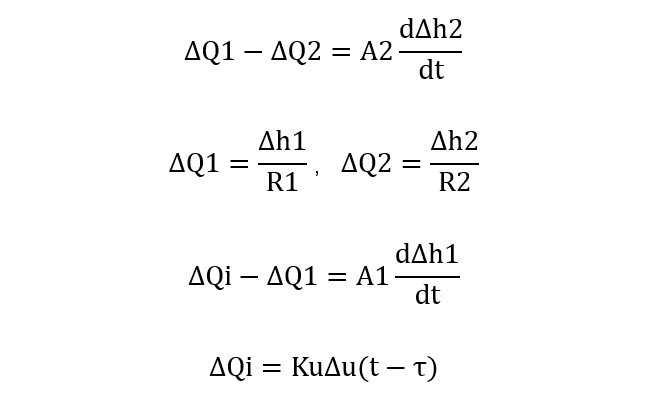
消掉中间变量,保留输入量Δu和输出量Δh2
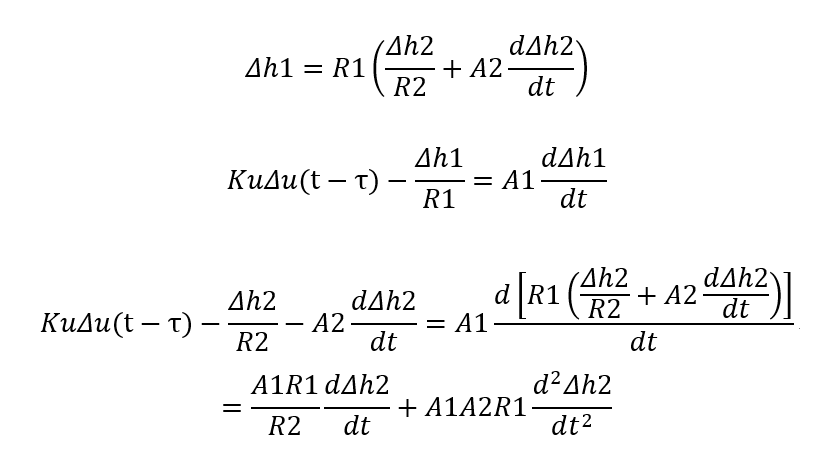
整理得到双容水槽微分方程:
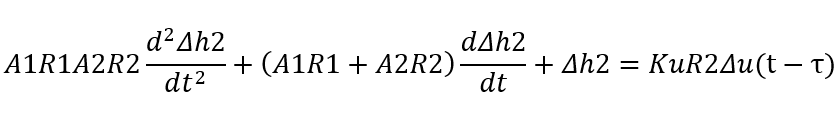
设T1=A1R1为第一个水槽时间常数,T2=A2R2为第二个水槽时间常数,K=KuR2为双容水槽传递系数。在零初始条件下,对微分方程两侧进行拉氏变换,得到双容水槽传递函数:
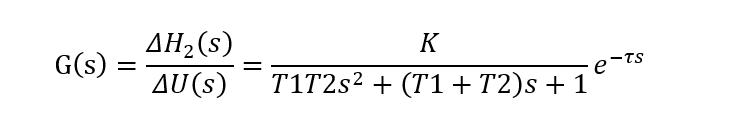
采用两个单容水槽串联结构求解双容水槽传递函数:
在无源网络的传递函数中,介绍了两个无源网络的串联形式,设两个无源网传递函数分别为G1(s),G2(s),当满足两个无源网络串联后,前后无负载效应,两个无源网串联后的传递函数G(s)= G1(s)G2(s)。
双容水槽模型中,第一个水槽的输出与第二个水槽的输入之间无负载效应,因此,双容水槽相当于两个单容水槽串联结构,双容水槽传递函数等于两个单容水槽传递函数相乘;
第一个单容水槽传递函数:
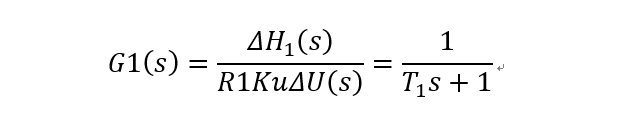
第二个水槽传递函数把输入量KuΔu换为ΔQ1o,
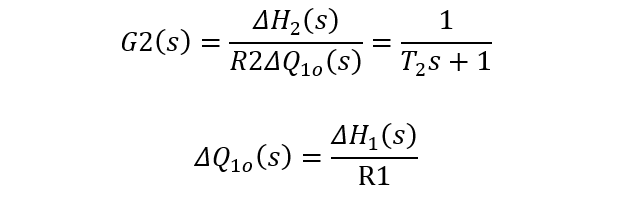
把两个传递函数相乘:
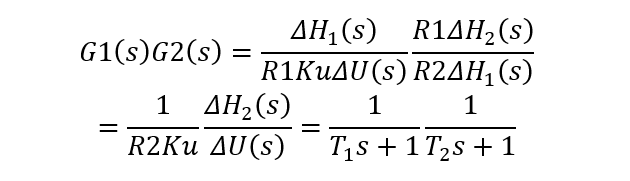
可获得两个单容水槽串联传递函数:
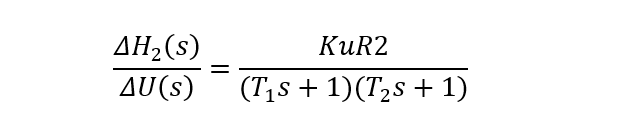
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
传递函数的定义是什么 传递函数的拉氏反变换是什么响应2024-02-01 8462
-
传递函数中的极点和零点有何影响?2023-09-19 3762
-
开环传递函数是怎样影响系统的?2023-07-11 5723
-
如何列写自控元件伺服电动机传递函数2023-03-10 4076
-
传递函数的频率特性2023-02-24 4174
-
模拟电路中传递函数的快速列写方法2019-04-20 11314
-
传递函数前言2018-11-28 1834
-
传递函数的频域辨识2017-10-26 1988
-
拓扑传递函数的列写2016-08-14 3181
-
基于Butterworth标准传递函数设计2009-06-11 922
-
电动执行机构传递函数的研究2009-03-17 1107
全部0条评论

快来发表一下你的评论吧 !

