PID控制原理详解

PID即：Proportional（比例）、Integral（积分）、Differential（微分）的缩写，PID控制算法是结合比例、积分和微分三种环节于一体的控制算法，它是连续系统中技术最为成熟、应用最为广泛的一种控制算法，该控制算法出现于20世纪30至40年代，适用于对被控对象模型了解不清楚的场合。实际运行的经验和理论的分析都表明，运用这种控制规律对许多工业过程进行控制时，都能得到比较满意的效果。PID控制的实质就是根据输入的偏差值，按照比例、积分、微分的函数关系进行运算，运算结果用以控制输出。

在实际控制系统中，通过P、I、D三个环节的不同组合，即可得到常用的各种调节规律，PID具有原理简单、鲁棒性强、适应性广等优点，即使在新型控制算法与控制规律不断产生的今天，PID作为最基本的控制方式仍占据重要的地位，显示出强大的生命力。

PID控制是一种经典的反馈控制算法，可以根据实际输出值与预期输出值之间的误差信号，及时调整控制输出值，从而实现对控制精度的提高。PID控制的主要原理包括比例控制、积分控制和微分控制。

比例控制（P控制）

比例控制是根据实际输出值与预期输出值之间的误差信号，按比例调整控制输出值，以实现对控制精度的提高。比例控制的输出量与误差成正比，即输出量P=Kp*ΔE，其中Kp是比例系数，ΔE为误差信号。

比例控制具有快速响应、控制精度高等优点，但是容易出现静态误差和振荡等问题。

积分控制（I控制）

积分控制是根据误差信号的积分值来调整控制输出量，以消除静态误差和提高稳态精度。积分控制的输出量与误差信号的积分值成正比，即输出量I=Ki*∫ΔEdt，其中Ki为积分系数。

积分控制能够消除静态误差，但是容易引起系统的超调和振荡等问题。

微分控制（D控制）

微分控制是根据误差信号的变化率来调整控制输出量，以提高控制系统的稳定性。微分控制的输出量与误差信号的变化率成正比，即输出量D=Kd*d（ΔE）/dt，其中Kd为微分系数。

微分控制能够提高系统的稳定性，但是容易引起系统的抖动和噪声等问题。

PID控制

PID控制将比例控制、积分控制和微分控制三种控制方式结合起来，以实现更为精确的控制。PID控制器的输出量为PID=KpΔE+Ki∫ΔEdt+Kd*d（ΔE）/dt，其中Kp、Ki和Kd分别为比例系数、积分系数和微分系数。

PID控制具有快速响应、控制精度高和稳态误差小等优点，是一种广泛应用于控制系统中的控制算法。但是，PID控制也存在一些问题，例如调节困难、参数选择不当容易引起系统的不稳定等问题。因此，在实际应用中，需要根据具体控

PID算法的执行流程是非常简单的，即利用反馈来检测偏差信号，并通过偏差信号来控制被控量。而控制器本身就是比例、积分、微分三个环节的加和。其功能框图如下：

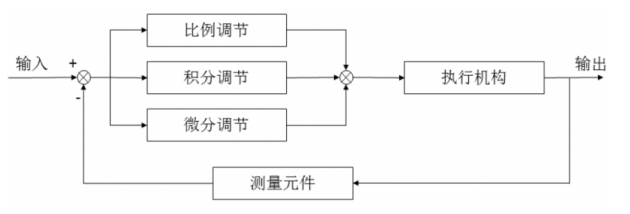
考虑在某个特定的时刻t，此时输入量为rin（t），输出量为rout（t），于是偏差就可计算为err（t）=rin（t）-rout（t）。于是PID的基本控制规律就可以表示为如下公式：

 

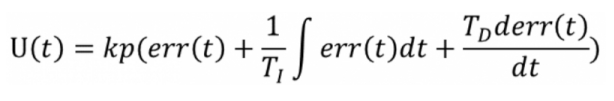
其中Kp为比例带，TI为积分时间，TD为微分时间。PID控制的基本原理就是如此。