关于安全可调稳压器设计教程

在LM350(LM317)可调稳压器的典型电路中，电位器通常是最不可靠的部分。当很少进行调整并且负载的安全性并不重要时，这可能不是一个很大的问题。但是，当想要进行频繁调整，或者事先不知道负载时该怎么办？

图1给出了LM350(LM317)可调稳压器在需要调整其输出电压时的典型使用。

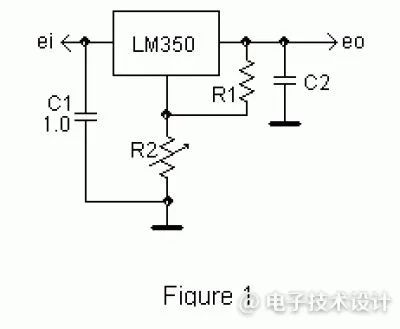图1：LM350(LM317)可调稳压器在需要调整输出电压时的典型使用。

该电压在此给出的大约为：

eo = Vref * (R2/R1 + 1)

电位器R2通常是电路中最不可靠的部分。如上面的表达式所示，电位计的击穿(例如，触点丢失、开路)会使R2的有效值最大化，而使输出电压也达到最大值——仅比输入电压低约1.5V。

当很少进行调整并且负载的安全性并不重要时，这可能不是一个很大的问题。但是，当我们想要进行频繁调整，或者事先不知道负载时(例如在实验室电源的情况下)，图2a中的电路可能是更好的选择。

图2a：可调稳压器的安全改进版本。

然而，该电路不能将其输出电压调节到下限Vref，这是它的局限性。

有几种安全可调稳压器的替代配置，它们或多或少地避免了越界的危险。最安全的情况是让输出电压下降到非常接近Vref，这需要3或4个额外的元器件(即电阻器和晶体管)，因此，让我们看一下图2b中具有更多折衷的配置。

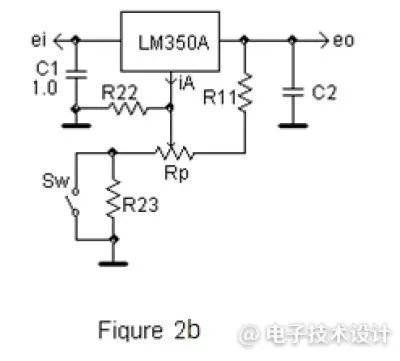图2b：安全可调稳压器的替代配置。

该电路可以将其输出电压调节到下限Vref。输出电压(如果电位器Rp发生击穿)约为2.5V，这是一个折衷值。

由于图2b中的电路计算不是很简单，因此此处将以Python代码的形式提供一些计算路径。

该电路有两个输出电压范围：从eo11到eo12，以及从eo21到eo22(见图3代码)。该范围是由开关Sw(例如nJFET、nFET或任何良好的机械簧片继电器)进行选择的。

请注意：如果电阻器R11和Rp太大而无法提供稳压器IC所需的最小负载(最大10mA)，那么如果总负载太轻，输出就可能会失控。

为避免这种情况，开始计算时为R11选择任何合适的值可能更明智。

还必须提供Rp值和范围。

以下代码给出了R22和R23的计算。

#-code-beginsR11=560 # OhmRpot=2180 # Ohm

eo11=1.25 #Veo12=5.6 #Veo21=5.4 #Veo22=23.0 #V

Vref=1.25 #Vprint()

LetK12 = eo12/Vref – 1K21 = eo21/Vref – 1K22 = eo22/Vref – 1Rp = Rpot

from math import sqrt

def checkEq(R11, R22, R23):Rx=R11 – Ra/K12if Rx != 0: print(“Err R11:”, Rx)

Rx=R22 R23/(R22+R23) – K21 (Rp+R11)if Rx != 0: print(“Err (2):”, Rx)

Rx=R11 – (R22*(Rp+R23)/(R22+Rp+R23) / K22)if Rx != 0: print(“Err (3):”, Rx)return

def par(r1,r2): return(r1*r2/(r1+r2))

eo=eo12R1 = R11R2 = R1*((eo/Vref) -1)R22 = R2*Rpot / (Rpot – R2)

eo=eo21 #5.1V#R1 = R11 + R21*Rpot / (R21 + Rpot)#R2 = R1*(eo/Vref -1)#R23 = R2

#eo=eo22 #24V ??

#R1 = R11#R2 = R23 + R22*Rpot / (R22 + Rpot)#eo = Vref*(R2/R1 + 1)#eo22 = eo

#Let K12 = eo12/Vref – 1K21 = eo21/Vref – 1K22 = eo22/Vref – 1Rp = RpotRa = par(Rp,R22)

w3=K22/K21A=w3*(R22 – K21*Rp) – R22B=w3*R22*(R22+Rp) – Rp*(w3*K21*(Rp+R22)-R22) – R22*R22C=Rp*R22*(0-w3*K21*(R22+Rp)-R22)

Q=BB – 4A*C#print(A, B, C, Q)if Q<0: exit(” Exit: Q<0, try another values for R11, Rpot, or ranges”)

R23_1 = (0-B + sqrt(Q)) /2/AR23_2 = (0-B – sqrt(Q)) /2/Aprint(” R23_1, R23_2=”, R23_1, R23_2)# since R23 should be > 0: if R23_1>0: R23=R23_1elif R23_2>0: R23=R23_2else: print(“Error: both R23_1, R23_2 are not positives”)

recalc eoij for a coherence checkeo12=Vref*(par(Rp,R22)/R11 +1)eo21=Vref*(par(R23,R22)/(Rp+R11) +1)eo22=Vref*(par(R22,R23+Rp)/R11 +1)# updateK12 = eo12/Vref – 1K21 = eo21/Vref – 1K22 = eo22/Vref – 1

print(“Fig2c:”, f” eo12={eo12:.2f}”, f” eo21={eo21:.2f}”, f” eo22={eo22:.2f}”)print(“Fig2c:”, f” Rpot={Rpot:.1f}”, f” R11={R11:.1f}”, f” R22={R22:.1f}”, f” R23={R23:.1f}”)checkEq(R11, R22, R23)

since the solution we got may be very sensitive due to a possible presence of a singular point in its vicinity (i.e. a small deviation of a resistor’s value can have large impact on the voltage) – hence 2 conclusions follows:# – tolerances of resistors R11, R22, R23 have to be not worse than 1%;# – the solution above has to be considered as a preliminary one, so we’ll make it more precise by the following code:

R23lim=100*R23R23=R23/3while R23 < R23lim:eo21_x=Vref*(par(R23,R22)/(Rp+R11) +1)eo22_x=Vref*(par(R22,R23+Rp)/R11 +1)if eo21_x – eo21 > 0.2: breakif abs(eo22 – eo22_x) < 0.1: break # if eo22-x – eo22 < 0.1: breakR23 += 10 # +10 Ohmelse: exit(“full cycle”) print( f” eo21={eo21_x:.2f}”, f” eo22={eo22_x:.2f}”, f” R23={R23:.1f}”)

#-end-of-code-

来自调节端的50μA(典型值)电流iA(代表误差项)，将在R23上产生压降。连同标称1.25V参考电压Vref，此压降决定了电位器Rp发生击穿时的输出电压：

eoBreak = iA * R22 + Vref

因此，当降低R22的值时，可以在某种程度上降低eoBreak的值。

— Peter Demchenko在维尔纽斯大学学习数学，并从事软件开发工作。