锁定放大器的基本原理

有时我们发现自己需要测量非常、非常低的电压信号——纳伏量级甚至更小。我们可能会认为这不应该是一个问题，并且理所当然地认为可以使用传统的运算放大器链来放大此类信号。

好吧，我们错了。因为我们忘记了噪音。

如果一个信号被放大，那么随之而来的就是噪声。因此，即使我们放大了所需信号，我们也无法将其与背景噪声区分开来。

在这种情况下，解决方案是锁定放大器。本文介绍了它们所依据的理论，以及它们的主要特征。

锁定放大器和噪声

假设您想测量 100 KHz 的 50 nV 正弦波。频率不是很高，因此示波器或万用表等常规仪器具有足够的带宽。另一方面，幅度非常低，因此当然需要一些放大。

在这里，我们可以使用低噪声放大器 (LNA)，例如AD8429，它的输入噪声为 2 (nV/\\sqrt{Hz})，带宽为 1.2 MHz，增益为 100。信号和噪声输出将分别为：

[s_{out}=s_{in}*G=50nV*100=5\\mu V]

[n_{out}=n_{in}*G=2 \\frac {nV}{\\sqrt{Hz} }*\\sqrt{1.2*10^6Hz}*100=219.089 \\mu V]

噪声比信号大几倍，因此即使使用具有良好噪声特性的放大器也无法正确测量信号。即使我们在放大之前添加一个很难实现的高 Q 滤波器，噪声仍然太高而无法从背景噪声中恢复信号。

我们需要一个新的解决方案——它的名字是锁定放大器。

什么是零差接收器？

在进入细节之前，让我们提醒自己一个相对古老的概念。

当信号通过天线发送时，它通常不会在其基带中发送，而是使用载波信号进行调制。该载波或参考信号可以从几 KHz 到几 MHz，具体取决于可用的技术、功耗和成本。

零差接收器（和发射器）仅使用一个频率来上下移动信号，而外差则使用中频。

基本零差接收器具有以下方面：

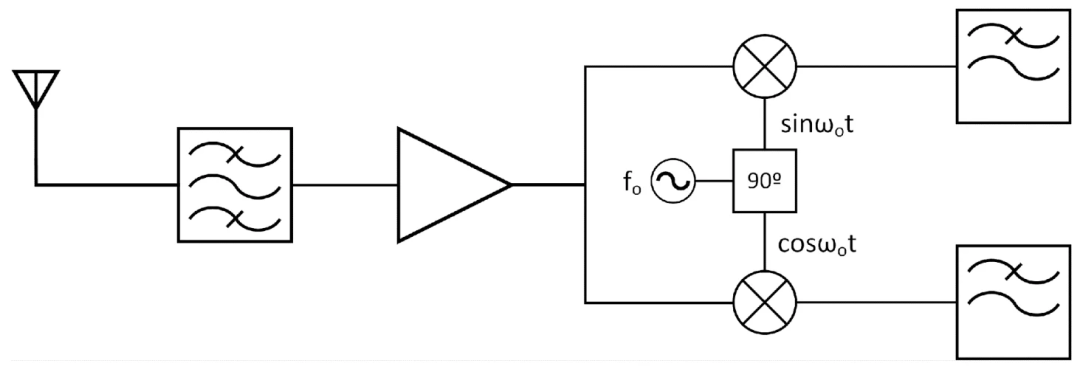
图 1. 零差接收器示意图

接收到的信号首先使用带通滤波器进行滤波，然后使用具有低噪声放大器 (LNA) 的放大器进行滤波。本地振荡器产生频率为 f o的参考信号。该信号偏移 90º，因此生成正交信号。

该接收器也称为 I/Q 解调器，因为它使用分量 I ((sin \\omega _ot)) 和 Q ((cos \\omega _ot))。

在最后阶段，使用低通滤波器滤除每个分量。

请记住这个概念，因为我们将使用它来理解锁定放大器。

时间与频域：两全其美

如果信号 (s(t)=A cos ( \\omega_st)) 是使用零差发射器发送的，则它与参考信号在接收器中的乘积方式相同，如下所示：

[s(t)*s_c(t)=(\\omega_st+\\phi_1 *cos(\\omega_ct+ \\phi_2)= \\frac {A}{2}(cos((\\omega_s+ \\omega_ct+ \\phi_1+ \\phi_2)+ cos( (\\omega_c- \\omega_s)t+ \\phi_2- \\phi_1)))]

因此，将两个信号相乘会生成两个新信号，它们分别在频率 (\\omega_c + \\omega_s) 和 (\\omega_c - \\omega_s) 处发生偏移。

我们可以用图形方式观察时域和频域的结果：

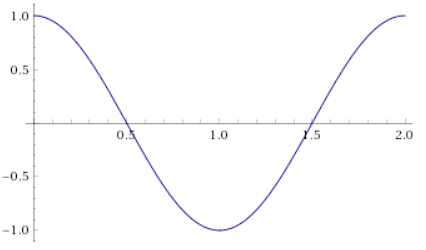
图 2. s(t) 通常是低频信号

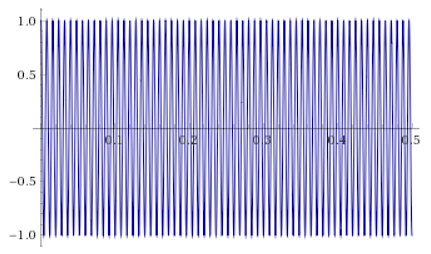
图 3. sc(t) 是精确生成的高频信号

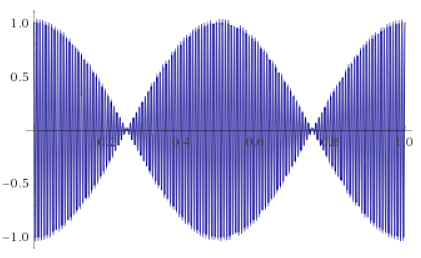
图 4. 结果中可以清楚地观察到慢速分量（包络）和快速分量（调制）的组合

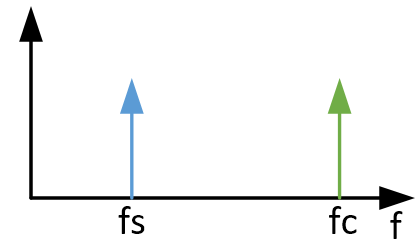
图 5. 正弦信号是频域中的纯音

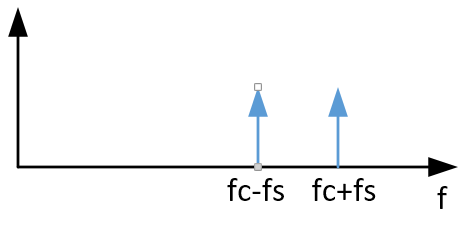
图 6. 一个信号的频率可以通过一个简单的操作来增加或减少

最相关的方面之一是相位信息成为 (\\phi_1 ) 的函数。因此，参考信号的相位质量将决定恢复信号的质量。

锁相放大器原理

图 7 显示了一个基本的锁定放大器。

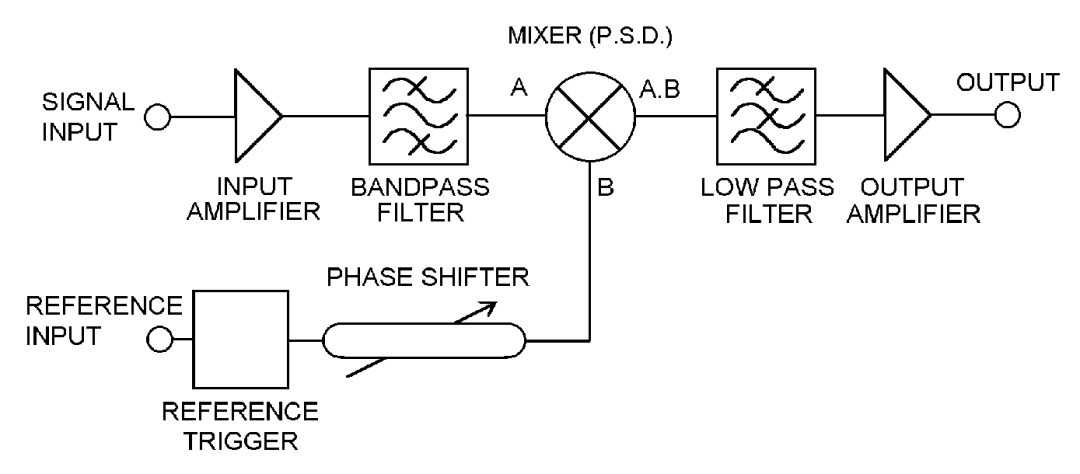
图 7. 一个基本的锁相放大器。图片由Signal Recovery提供

你觉得这很熟悉吗？

它与零差接收器非常相似，但有一些细微差别。系统的核心是移相器和乘法器。这种设置保证了输出信号与我们要测量的信号一致，并且没有其他信号干扰它。

相敏检测 (PSD)

乘法器块也称为混频器或相敏检测器。这是因为输出信号取决于参考信号和测量信号之间的相位差。

在常规情况下，参考信号频率将与测量的频率相同——即 (\\omega_s= \\omega_c )——当两者相乘时。结果将是：

[s(t)*s_ct=\\frac{A}{2}(cos( (2\\omega_s)t+ \\phi_1+\\phi_2)+ cos(\\phi_2-\\phi_1))))]

结果是两个术语的组合：

• (2f_s) 处的高频信号将被过滤掉，然后
• 直流信号 (\\frac{A}{2}cos :cos(\\phi_2+\\phi_1)) 与参考信号和所需信号之间的相移成正比

因此，锁定放大器将始终产生连续信号。

动态储备：我的信号可以有多小？

“动态储备”是锁定放大器中使用的一个术语，用于定义它们从确定的噪声水平恢复信号的能力。它的常规定义是最大可容忍噪声信号与满量程信号的比值。

动态储备通常以对数标度 (dB) 表示。例如，在 1 µV 满量程上 120 dB 的动态储备意味着噪声可以高达 1V，而不会使放大链饱和。

需要注意的是，动态储备取决于所选的满量程，否则锁定放大器必须能够在选择大满量程值时测量巨大的输入信号。

基本锁相放大器回顾

我希望这篇文章能帮助您更好地了解锁定放大器及其用途。我们可以将我们的发现总结为以下几点：

• 基于零差收发器概念的锁相放大器是在存在大量噪声的情况下测量极低电压时的唯一解决方案。
• 锁定放大器始终提供与测量信号和参考信号之间的相移成比例的连续信号。
• 参考信号的好坏决定了信号检测的成功与否。