PID控制算法详解(一)

一、PID的由来：

过去都是采用位式(两位式‘开关量’)控制方法，即位式控制算法只有两种输出信号(H/L)，即开或关、0或1。且位式控制只考察控制对象当前的状态量，而对于实际对象来说都具有惯性，会使得调节器一直在输出，即输出一直在预期值附近波动，无法达到精准控制。

由此，需要有一种控制算法，不仅能对控制对象当前输出量的控制，还能对过去历史的规律的“总结”(消除环境等因素造成的静态误差)以及对未来对象输出的提前预判，对对象提前进行控制，使得输出能够尽快达到预期值并稳定下来(正如那句话所说，‘不要等到已经发生了才开始控制，往往会来不及的’)。

二、PID内容：

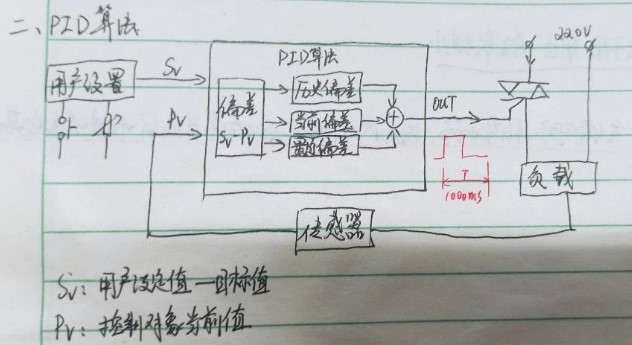
相信对学习过PID控制的小伙伴对上面这张图并不陌生吧。这是一个典型的PID控制，对于PID控制技术，在本科学习时老师在第一节课就和我们说，PID控制技术就是让系统从0到1的过程，如何让它在这个过程中快速、稳定地达到1，并且稳态之后能够保持预期值的一种控制技术。以下简单说明PID算法的形成：

[比例]-Kp

1、从开机开始，传感器的所有采样数据序列：

x1,x2x3……xn-3,xn-2,xn-1,xn

2、序列采样点的数据序列，可以挖掘出的信息：

1)err=给定值-反馈值：如果err>0，当前未达到给定值

如果err=0，当前达到给定值

如果err<0，当前大于给定值

但是会发现一个问题，比例控制只会在有误差的情况下起作用，如果单纯只采用比例控制，那么按照自己的理解来说等系统稳定之后，误差为零，控制器将不会有输出，做仿真实验时却发现问题，如下(以一阶惯性系统为控制对象)：

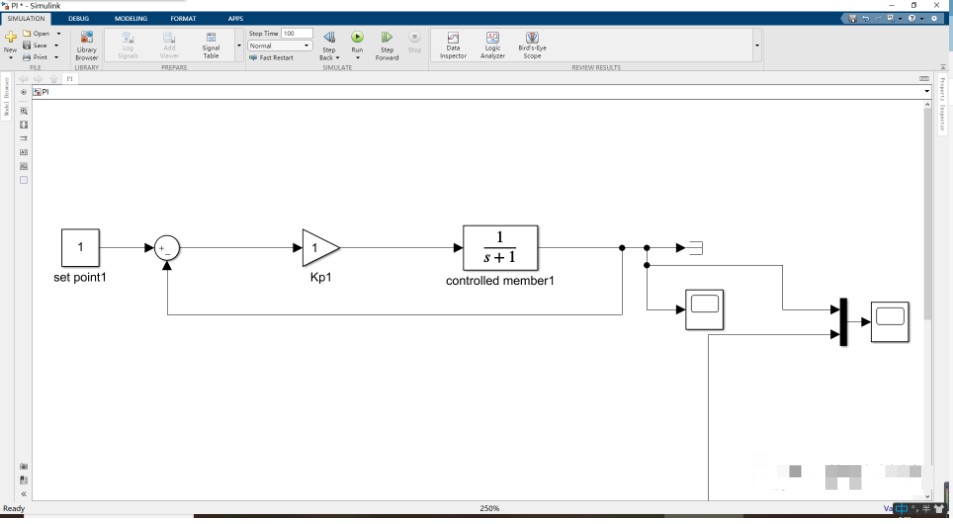
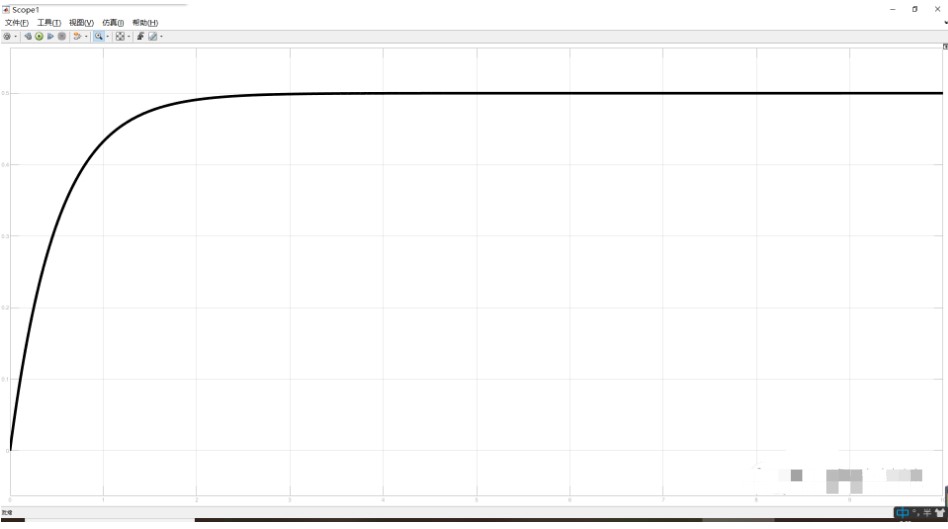
其系统稳定之后输出并不为零，而是小于预期值。看了韩京清教授编写的自抗扰控制技术之后才了解到，这是由于稳态误差的存在。

由上图的仿真图可知：

x1 = Kp * err = Kp * (x0 - y);

其闭环传递函数为：

1/(s+2)

当时间趋近于无穷大时，也就是s趋近于0时，其输出值为1/2，这个偏离期望值的这个量就叫闭环系统的稳态误差或者静差，从表达式可以看出，如果增大比例，如kp=100会发现其传递函数变为:

100/(s + 101);

其输出稳态误差变为100/101，远小于kp=1时的1/2。而且还能发现其达到稳定值的调节时间大约是之前的1/50倍。

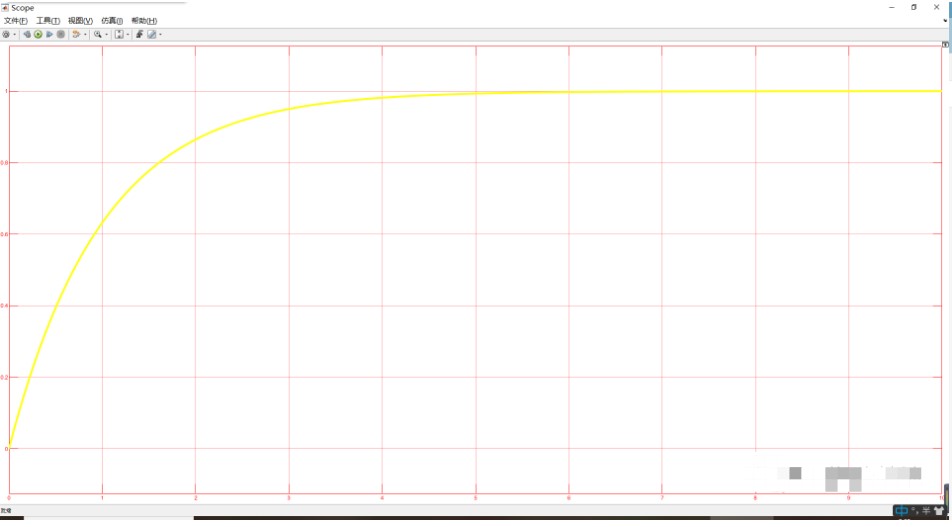
那如果我将KP的值设为很大那这样不就能够达到PID控制的要求了吗?非也，查阅了相关资料之后发现，线性模型是对非线性对象在工作点附近的近似，所以kp如果设置很大就很容易使系统的运动跃出线性近似范围而产生难以驾驭的复杂行为。所以kp的设定不能无限制增大。而且通过其表达式还能发现，控制对象的表达式中分母的常数项就是稳态误差产生的源泉，只要这个常数项不为零，那么稳态误差就不会消除，但是对于我们的控制对象，它的表达式一般都是非常复杂的，想必这一项也不太可能为零。

那么问题就来了，kp又不能设置太大，那么稳态误差就会一直存在，必须想办法用一种方式将稳态误差消除或者减小，这个时候，积分项，也就是PID中的I就出现了。

三、总结：

1)位式控制算法所出现的弊端引发了PID控制算法的出现;

2)稳态误差的产生主要是由控制对象产生的;

3)KP的设定值越大，能够有效改善系统输出的响应时间和稳态误差值，但是也不能无限制增大kp的值。