PID控制算法详解(二)

一、积分理解

在上一章的内容中说到了PID的由来以及kp的作用和缺陷，由此引出了ki的出现。为了消除控制对象在PID控制中出现的静态误差，我们通常采用再加误差的积分。

积分的作用：其输出量与输入量对时间的积分成正比。如果输入突变，输出值要等一定时间之后才等于，故由滞后作用。输出积累一段时间之后，即使使输入为零，输出也将保持原值不变，即具有记忆功能。只有当输入反相时，输出才反相积分而下降。

那么为什么要引入积分项就能消除系统所带来的稳态误差呢?初步理解就是积分项是对从开始起，不断累加各个采样时刻的误差，由此，将系统所产生的稳态误差转移到积分上，就消除了系统输出的静差。下面就通过理论与仿真来具体分析：

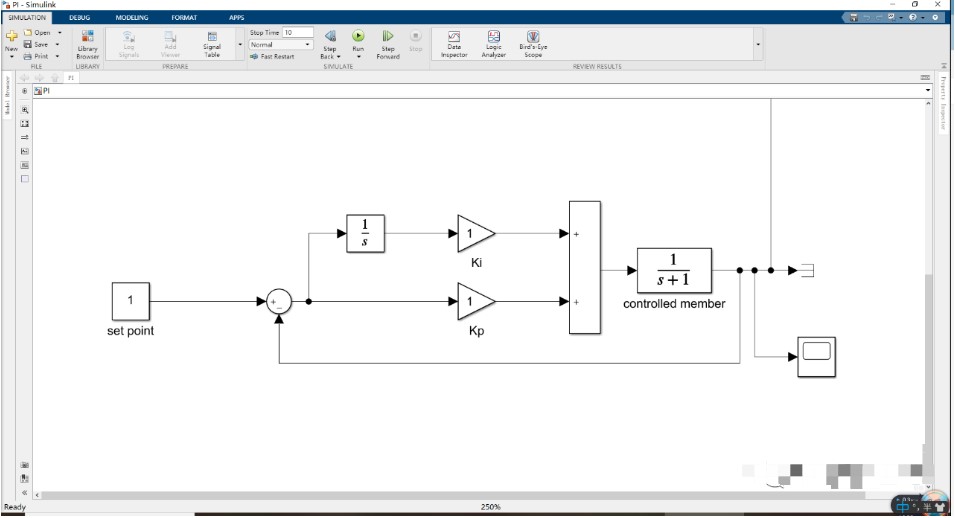
为保证仿真的有效性，仿真的控制对象与只采用比例P控制对象均为一阶惯性函数。系统输出如下图所示：

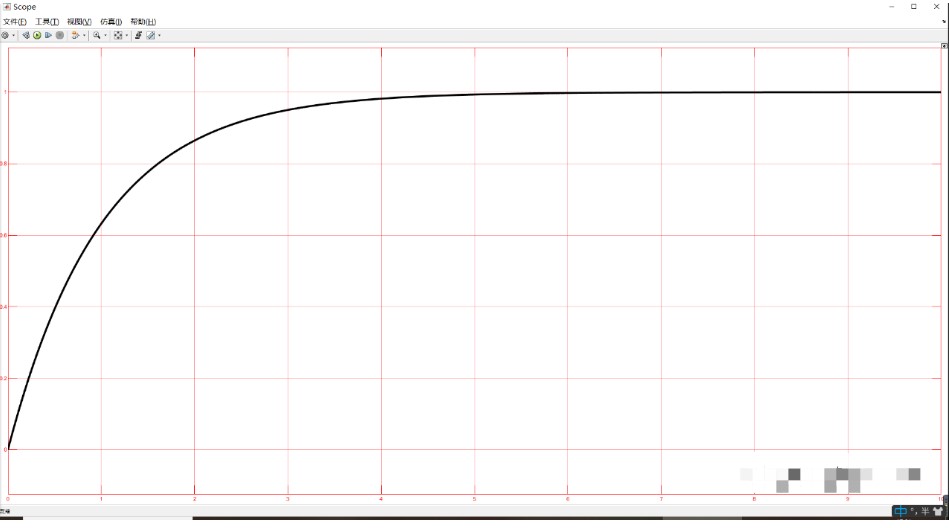
可以从仿真看出，输出逐步趋于期望值最后并稳定于1。其闭环传递函数为：

1/(s+1);

当s趋于0，即时间趋于无穷大时，其输出为1。但是在这里会发现一个巧妙的现象，PI控制的传递函数的分子刚好是控制对象的分母，将积分项的参数设置为Ki，那么其表达式为:

(S+Ki)/(S^2+2S+Ki);

那就是说，Ki我设置什么值都行，但是在仿真的时候，我将Ki的值设置为100的时候，系统的输出出现了抖动，如下图所示：

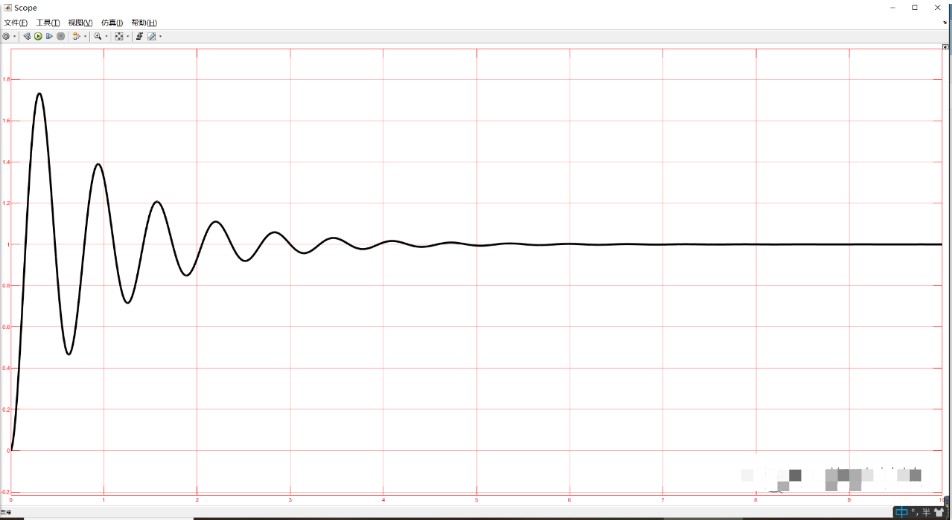
按照其闭环传递函数ki的值与最终的输出好像关系不大，但是为什么输出出现抖动呢?查阅资料之后发现，积分前一个采样周期计算出的误差作用于下一个采样周期，所以就会出现抖动，而且这个抖动会一直存在，不会消失，只是时间变长之后，这个存在的误差就忽略不计了。所以ki的参数不能设置太大，那么应该如何设置呢?

看了相关的书籍之后，(从时域分析)要让系统响应无震荡和超调，那就要让系统处于一个临界阻尼状态。欠阻尼状态理解为系统的最佳状态，即ε要在[0,1]之间取值，二阶系统在欠阻尼时的响应为衰减震荡的，所以必然存在超调。从书本上了解到对于一个二阶系统在单位阶跃输入信号作用下的传递函数为:

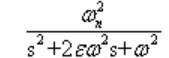
对于仿真系统而言，其ki的取值应该为ε>1。但是会发现其值为100，已经大于1了，但是系统存在很大震荡。这个时候自己的理解就是经验试凑，逐步逼近最优值。最后试凑出来的参数为kp=1，ki=1.3，输出波形如下图所示，但是会发现系统的系统的响应变慢了。

二、总结：

1.积分项的加入能够消除控制对象所产生的的静态误差，将静差转移到积分项上;

2.积分项从整体来看是有记忆功能的，不断累积系统所产生的的误差，但是细看，积分项的作用只是基于前一个采样周期所产生的误差作用于下一个周期或者下下个周期，因为积分项有延迟作用;

3.由于积分项的延迟作用，在一定程度上影响了系统的响应，所以PID控制中的微分项I就出现了。

三、猜想：

既然积分项有延迟作用，那如果我直接在积分项后面加入输出的反馈，用于消除积分的延迟问题，岂不是能够解决积分的延迟问题。