脉冲电路到底有何用途和特点？

在电子电路中，电源、放大、振荡和调制电路被称为模拟电子电路，因为它们加工和处理的是连续变化的模拟信号。 电子电路中另一大类电路的数字电子电路。 它加工和处理的对象是不连续变化的数字信号。 数字电子电路又可分成脉冲电路和数字逻辑电路，它们处理的都是不连续的脉冲信号。 脉冲电路是专门用来产生电脉冲和对电脉冲进行放大、变换和整形的电路。 家用电器中的定时器、报警器、电子开关、电子钟表、电子玩具以及电子医疗器具等，都要用到脉冲电路。

电脉冲有各式各样的形状，有矩形、三角形、锯齿形、钟形、阶梯形和尖顶形的，最具有代表性的是矩形脉冲。 要说明一个矩形脉冲的特性可以用脉冲幅度 Um 、脉冲周期 T 或频率 f 、脉冲前沿 t r 、脉冲后沿 t f 和脉冲宽度 t k 来表示。 如果一个脉冲的宽度 t k =1 ／ 2T ，它就是一个方波。
脉冲电路和放大振荡电路最大的不同点，或者说脉冲电路的特点是：脉冲电路中的晶体管是工作在开关状态的。 大多数情况下，晶体管是工作在特性曲线的饱和区或截止区的，所以脉冲电路有时也叫开关电路。 从所用的晶体管也可以看出来，在工作频率较高时都采用专用的开关管，如 2AK 、 2CK 、DK 、 3AK 型管，只有在工作频率较低时才使用一般的晶体管。

就拿脉冲电路中最常用的反相器电路（下图1）来说，从电路形式上看，它和放大电路中的共发射电路很相似。 在放大电路中，基极电阻 R b2 是接到正电源上以取得基极偏压； 而这个电路中，为了保证电路可靠地截止， R b2 是接到一个负电源上的，而且 R b1 和 R b2 的数值是按晶体管能可靠地进入饱和区或止区的要求计算出来的。 不仅如此，为了使晶体管开关速度更快，在基极上还加有加速电容 C ，在脉前沿产生正向尖脉冲可使晶体管快速进入导通并饱和； 在脉冲后沿产生负向尖脉冲使晶体管快速进入截止状态。 除了射极输出器是个特例，脉冲电路中的晶体管都是工作在开关状态的，这是一个特点。

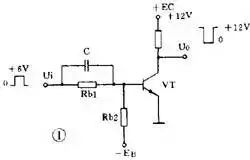
脉冲电路的另一个特点是一定有电容器（用电感较少）作关键元件，脉冲的产生、波形的变换都离不开电容器的充放电。

产生脉冲的多谐振荡器

脉冲有各种各样的用途，有对电路起开关作用的控制脉冲，有起统帅全局作用的时钟脉冲，有做计数用的计数脉冲，有起触发启动作用的触发脉冲等等。 不管是什么脉冲，都是由脉冲信号发生器产生的，而且大多是短形脉冲或以矩形脉冲为原型变换成的。 因为矩形脉冲含有丰富的谐波，所以脉冲信号发生器也叫自激多谐振荡器或简称多谐振荡器。 如果用门来作比喻，多谐振荡器输出端时开时闭的状态可以把多谐振荡器比作宾馆的自动旋转门，它不需要人去推动，总是不停地开门和关门。

（ 1 ）集基耦合多谐振荡器

下图2是一个典型的分立元件集基耦合多谐振荡器。 它由两个晶体管反相器经 RC 电路交叉耦合接成正反馈电路组成。 两个电容器交替充放电使两管交替导通和截止，使电路不停地从一个状态自动翻转到另一个状态，形成自激振荡。 从 A 点或 B 点可得到输出脉冲。 当 R b1 =R b2 =R ， C b1 =C b2 =C 时，输出是幅度接近 E 的方波，脉冲周期 T=1.4RC 。 如果两边不对称，则输出是矩形脉冲。

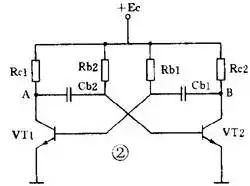
（ 2 ） RC 环形振荡器

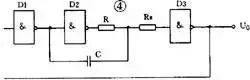
下图 4 是常用的 RC 环形振荡器。 它用奇数个门、首尾相连组成闭环形，环路中有 RC 延时电路。 图中 RS 是保护电阻， R 和 C 是延时电路元件，它们的数值决定脉冲周期。 输出脉冲周期 T=2.2RC 。 如果把 R 换成电位器，就成为脉冲频率可调的多谐振荡器。 因为这种电路简单可靠，使用方便，频率范围宽，可以从几赫变化到几兆赫，所以被广泛应用。

脉冲变换和整形电路

脉冲在工作中有时需要变换波形或幅度，如把矩形脉冲变成三角波或尖脉冲等，具有这种功能的电路就叫变换电路。 脉冲在传送中会造成失真，因此常常要对波形不好的脉冲进行修整，使它整旧如新，具有这种功能的电路就叫整形电路。

（ 1 ）微分电路

微分电路是脉冲电路中最常用的波形变换电路，它和放大电路中的 RC 耦合电路很相似，见图 5 。 当电路时间常数 τ=RC<

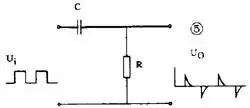
（ 2 ）积分电路

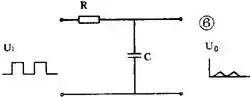
把图 5 中的 R 和 C 互换，并使 τ=RC>>t k ，电路就成为积分电路，见图 6 。 当输入矩形脉冲时，由于电容器充放电很慢，输出得到的是一串幅度较低的近似三角形的脉冲波。

（3） 宽度限制器

能限制脉冲幅值的电路称为限幅器或削波器。 图 7 是用二极管和电阻组成的上限幅电路。 它能把输入的正向脉冲削掉。 如果把二极管反接，就成为削掉负脉冲的下限幅电路。

用二极带或三极管等非线性器件可组成各种限幅器，或是变换波形（如把输入脉冲变成方波、梯形波、尖脉冲等），或是对脉冲整形（如把输入高低不平的脉冲系列削平成为整齐的脉冲系列等）。

（ 4 ）箝位器

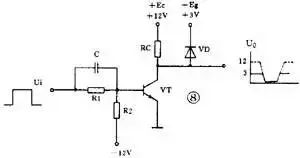
能把脉冲电压维持在某个数值上而使波形保持不变的电路称为箝位器。 它也是整形电路的一种。 例如电视信号在传输过程中会造成失真，为了使脉冲波形恢复原样，接收机里就要用箝位电路把波形顶部箝制在某个固定电平上。 下图 8 中反相器输出端上就有一个箝位二极管 VD 。 如果没有这个二极管，输出脉冲高电平应该是 12 伏，现在增加了箝位二极管，输出脉冲高电平被箝制在 3 伏上。

此外，象反相器、射极输出器等电路也有“整旧如新”的作用，也可认为是整形电路。

寄存二进制数码的单元电路

有记忆功能的双稳电路多谐振荡器的输出总是时高时低地变换，所以它也叫无稳态电路。 另一种双稳态电路就截然不同，双稳电路有两个输出端，它们总是处于相反的状态：一个是高电平，另一个必定是低电平。 它的特点是如果没有外来的触发，输出状态能一直保持不变。 所以常被用作寄存二进制数码的单元电路。

（ 1 ）集基耦合双稳电路

下图 9 是用分立元件组成的集基耦合双稳电路。 它由一对用电阻交叉耦合的反相器组成。 它的两个管子总是一管截止一管饱和，例如当 VT1 管饱和时 VT2 管就截止，这时 A 点是低电平 B 点是高电平。 如果没有外来的触发信号，它就保持这种状态不变。 如把高电平表示数字信号“ 1 ”，低电平表示“ 0 ”，那么这时就可以认为双稳电路已经把数字信号“ 1 ”寄存在 B 端了。

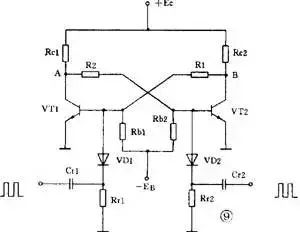
电路的基极分别加有微分电路。 如果在 VT1 基极加上一个负脉冲（称为触发脉冲），就会使 VT1 基极电位下降，由于正反馈的作用，使 VT1 很快从饱和转入截止， VT2 从截止转入饱和。 于是双稳电路翻转成 A 端为“ 1 ”， B 端为“ 0 ”，并一直保持下去。

（ 2 ）触发脉冲的触发方式和极性

双稳电路的触发电路形式和触发脉冲极性选择比较复杂。 从触发方式看，因为有直流触发（电位触发）和交流触发（边沿触发）的分别，所以触发电路形式各有不同。 从脉冲极性看，也是随着晶体管极性、触发脉冲加在哪个管子（饱和管还是截止管）上、哪个极上（基极还是集电极）而变化的。 在实际应用中，因为微分电路能容易地得到尖脉冲，触发效果较好，所以都用交流触发方式。 触发脉冲所加的位置多数是加在饱和管的基极上。 所以使用 NPN 管的双稳电路所加的是负脉冲，而 PNP 管双稳电路所加的是正脉冲。

（ 3 ）集成触发器除了用分立元件外，也可以用集成门电路组成双稳电路。 但实际上因为目前有大量的集成化双稳触发器产品可供选用，如 R—S 触发器、 D 触发器、 J － K 触发器等等，所以一般不使用门电路搭成的双稳电路而直接选用现成产品。

有延时功能的单稳电路

无稳电路有 2 个暂稳态而没有稳态，双稳电路则有 2 个稳态而没有暂稳态。 脉冲电路中常用的第 3 种电路叫单稳电路，它有一个稳态和一个暂稳态。 如果也用门来作比喻，单稳电路可以看成是一扇弹簧门，平时它总是关着的，“关”是它的稳态。 当有人推它或拉它时门就打开，但由于弹力作用，门很快又自动关上，恢复到原来的状态。 所以“开”是它的暂稳态。 单稳电路常被用作定时、延时控制以及整形等。

（ 1 ）集基耦合单稳电路

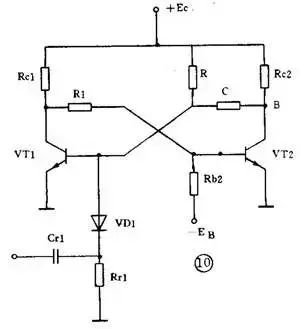
图 10 是一个典型的集基耦合单稳电路。 它也是由两级反相器交叉耦合而成的正反馈电路。 它的一半和多谐振荡器相似，另一半和双稳电路相似，再加它也有一个微分触发电路，所以可以想象出它是半个无稳电路和半个双稳电路凑合成的，它应该有一个稳态和一个暂稳态。 平时它总是一管（ VT1 ）饱和，另一管（ VT2 ）截止，这就是它的稳态。 当输入一个触发脉冲后，电路便翻转到另一种状态，但这种状态只能维持不长的时间，很快它又恢复到原来的状态。 电路暂稳态的时间是由延时元件 R 和 C 的数值决定的：t t =0.7RC 。

（ 2 ）集成化单稳电路

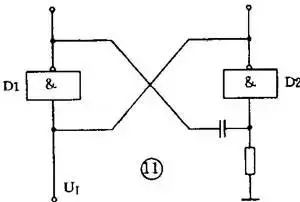
用集成门电路也可组成单稳电路。 图 11 是微分型单稳电路，它用 2 个与非门交叉连接，门 1 输出到门 2 是用微分电路耦合，门 2 输出到门 1 是直接耦合，触发脉冲加到门 1 的另一个输入端 U I 。 它的暂稳态时间即定时时间为：t t = （ 0.7 ～ 1.3 ） RC 。

脉冲电路的读图要点

①、脉冲电路的特点是工作在开关状态，它的输入输出都是脉冲，因此分析时要抓住关键，把主次电路区分开，先认定主电路的功能，再分析辅助电路的作用。
②、从电路结构上抓关键找异同。 前面介绍了集基耦合方式的三种基本单元电路，它们都由双管反相器构成正反馈电路，这是它们的相同点。 但细分析起来它们还是各有特点的：无稳和双稳电路虽然都有对称形式，但无稳电路是用电容耦合，双稳是用电阻直接耦合（有时并联有加速电容，容量一般都很小）； 而且双稳电路一般都有触发电路（双端或单端触发）； 单稳电路就很好认，它是不对称的，兼有双稳和单稳的形式。 这样一分析，三种电路就很好区别了。

③、脉冲电路中，脉冲的生成、变换和整形都和电容器的充、放电有关，电路的时间常数即 R 和 C 的数值对确定电路的性质有极重要的意义，这一点尤为重要。

　　审核编辑：汤梓红